Урок геометрії у 8 класі "Крокуючи за Піфагором"

Про матеріал

Урок математики у 8 класі – урок однієї теореми Мета: навчальна: систематизувати відомості про прямокутний трикутник; формувати навички знаходження різних способів доведення теореми Піфагора; показати застосування набутих знань в практичній діяльності; розвивальна: розвивати просторову уяву, вміння аналізувати, робити висновки, працювати творчо; виховна: виховувати активність, увагу та спостережливість. Тип уроку: урок однієї теореми. Обладнання: підручник, косинець, портрет Піфагора, кольорова крейда, кольорові стрічки.

Перегляд файлу

Урок математики у 8 класі –

урок однієї теореми

Підготувала:

учитель математики

Мистицької ЗОШ І-ІІ ст

Новіцька М.І.

Тема. Теорема Піфагора

Мета: навчальна: систематизувати відомості про прямокутний трикутник; формувати навички знаходження різних способів доведення теореми Піфагора; показати застосування набутих знань в практичній діяльності;

розвивальна: розвивати просторову уяву, вміння аналізувати, робити висновки, працювати творчо;

виховна: виховувати активність, увагу та спостережливість.

Тип уроку: урок однієї теореми.

Обладнання: підручник, косинець, портрет Піфагора, кольорова крейда, кольорові стрічки.

Хід уроку

Гарно прибраний клас. На стіні висить портрет Піфагора, На дошці із кольорових стрічок зроблено прямокутний трикутник, і напис:

«Мов світла промінь в темну пору,

Приходить істина до нас,

Як теорема Піфагора

Вона несхибна повсякчас».

І.Організаційний етап.

Вступне слово вчителя.

Сьогоднішній урок незвичайний. Він пов'язаний зі знаннями, яке виробило людство близько 4000 років. Дані знання дуже важливі, бо вони допомагали і допомагають людям будувати споруди, які зберігаються тисячоліттями. Це такі споруди, як єгипетські піраміди, храми та інші пам'ятки минулого. Цей урок присвячений одній єдиній теоремі Піфагора, доведенням якої займалися і займаються математики всіх країн. На цей час відомо близько тисячі доведень. Ми зупинимося на декількох. На минулому уроці ми доводили теорему за підручником , а на цьому уроці познайомимося з іншими доведеннями. Це Дасть вам не тільки краще розуміння, а і допоможе запам'ятати на все життя теорему, яка використовується в науці та житті. Запишіть тему уроку «ТеоремаПіфагора».
ІІ. Актуалізація опорних знань.

Евристична бесіда з класом (за технологією «Мікрофон»):

Що таке трикутник?
Які є види трикутників?
Який трикутник називається прямокутним?
Як називаються сторони прямокутного трикутника?
Намалюйте на дошці рівнобедрений прямокутний трикутник і назвіть усі його сторони та градусні міри кутів цього трикутника.
Сформулюйте теорему Піфагора

ІІІ.Формування мети й завдань уроку.

Теорема Піфагора – одна з основних у евклідовій геометрії. Завдяки їй можна довести та розв’язати не одну задачу. Тому її потрібно добре засвоїти. Сьогодні у нас урок однієї теореми, на якому ми закріпимо знання про теорему Піфагора, розв’яжемо задачі практичного змісту на використання цієї теореми.

А епіграфом нашого уроку пропоную взяти наступні слова великого Піфагора: «Добре засвоєна мудрість не забувається ніколи» Піфагор.

ІV. Перевірка домашнього завдання.(Усний журнал)

Ви вдома готували усний журнал про математика, іменем якого названа ця теорема.

1 учень.

Цього міцного юнака з товстою шиєю та коротким носом, справжнього забіяку, судді однієї з перших олімпіад не хотіли допускати до змагань, тому що Піфагор був малий на зріст. Але йому вдалося побитися зі своїми супротивниками та ще й перемогти. За деякими даними, Піфагор народився близько 580 р. до н.е. у Стародавній Греції на острові Самос, а помер у 500 р. до н. е.

Про життя вченого відомо небагато, але з його ім'ям пов'язаний ряд легенд. Розповідають, що він багато подорожував, був у Індії, Єгипті, Вавилоні, вивчав стародавню культуру й досягнення науки різних країн. Повернувшись на батьківщину, він організував гурток з молоді – представників аристократії. У гурток приймали з великими почестями після випробувань. Кожен, хто приходив у гурток, відмовлявся від свого майна й обіцяв зберігати в таємниці вчення засновника.

Так на півдні Італії, що була на той час грецькою колонією, виникла так звана Піфагорійська школа. Ті, хто хотів потрапити до неї, повинні були мовчати протягом п'яти років, тільки після цього їх зараховували. Та, незважаючи на незвичайний і жорстокий іспит, багато хто прагнув потрапити до цієї школи.

Піфагорійці займалися математикою, філософією, природничими науками. Вони багато винайшли в арифметиці й геометрії. У школі існував декрет, за яким авторство усіх математичних робіт присвоювалося Піфагору.

За однією з версій він був убитий під час народного повстання.

Після його смерті учні оточили ім'я свого вчителя різноманітними легендами. Тому встановити правду про звички й характер Піфагора неможливо.

2 учень.

1. Піфагор першим з грецьких математиків вивчав пропорцію та найпростіші види прогресій: арифметичну, геометричну, гармонічну.

2. Піфагор першим використав метод доведення від супротивного.

3. Він створив елементарні принципи побудови правильних многогранників, які назвав космічними фігурами.

4. Піфагор вважав, що куля найдосконаліша з усіх геометричних тіл і що Земля повинна мати форму кулі.

Особливу увагу Піфагор приділяв числам.

Він вважав, що число 5 символізує колір, 6 – холод, 7 – розум, 8 – кохання, дружбу, 9 – постійність, 13 і 14 були ненависними числами.

Парні числа вважалися нещасливими, а непарні – щасливими. ця піфагорійська традиція збереглася і зараз. Вважається, що треба дарувати букет з непарною кількістю квіток.

Ірраціональні числа також відкрив Піфагор, шукаючи діагональ квадрата зі стороною 1.

Також серед чисел виділяють піфагорові трійки чисел. Це трійки чисел, що задовольняють рівняння виду a² + b² = c² , де а, b, с – взаємно прості числа.

3, 4, 5; 5, 12, 13; 15, 8, 17.

Знання піфагорових трійок може допомогти спростити обчислення невідомих сторін трикутників.

Землеміри Стародавнього Єгипту для побудови прямого кута користувалися таким способом. Мотузку ділили вузлами на 12 рівних частин і кінці зв'язували. Потім її розкладали на землі так, щоб утворився трикутник зі сторонами 3, 4, 5 поділок. Кут трикутника, протилежний стороні, що має 5 поділок, - прямий. Тому прямокутний трикутник зі сторонами 3, 4, 5 одиниць називають єгипетським, або піфагоровим.

V. Суд над прямокутним трикутником.

Прямокутний трикутник — одна з перших геометричних фігур, про властивості якої людство дізналось ще в давнину. Задачі про трикутник знаходять у давньоєгипетських папірусах, старовинних індійських книгах.

$C:\Program Files\Microsoft Office\MEDIA\CAGCAT10\j0300840.wmf$ Учитель: Сьогодні в нас зібралося товариство трикутників, яке обурилось тим, що прямокутному трикутнику у 8-му класі присвячується ціла тема, а всім іншим трикутникам – гострокутному, тупокутному, рівнобедреному й навіть правильному – не відводять певної уваги в курсі геометрії.

Усе трикутне товариство зібралося на судове засідання.

Слово для звинувачення взяв правильний трикутник.

Правильний трикутник: Вельмишановні судді! (звертається до учнів класу). Наше товариство зібралось, щоб обговорити непристойну для члена нашого товариства поведінку прямокутного трикутника. Останнім часом він вважає себе основою геометрії, хвалиться, а все тому, що бачите:

1. Сума двох його гострих кутів дорівнює 90°.

2. Його сторони мають спеціальну назву: гіпотенуза, катет.

3. Якщо у всіх порядних трикутників центр описаного кола не належить стороні,то в нього він лежить на гіпотенузі, та ще й на її середині.

4. Для нього існують три спеціальні ознаки рівності трикутників, які належить тільки йому одному.

Враховуючи вище сказане, вимагаю від імені нашого товариства виключити прямокутний трикутник з товариства трикутників.

Тупокутний трикутник: Справді, він такий! Вважає себе унікальним, неповторним, необхідним усьому людству. А чим я, тупокутний трикутник, гірший?

Прямокутний трикутник: Друзі! Згадаймо наскільки різноманітне моє застосування в житті! Прямокутний трикутник застосовують у техніці, будівництві. А різні вимірювальні прилади? Достатньо згадати, що всі трикутники, які випускає наша промисловість і якими користуються в роботі – прямокутні. Без знань властивостей, які мають мої елементи, не можна розв’язати багатьох практичних задач.

Тупокутний трикутник: А ви б почули, що говорить прямокутний трикутник у зв’язку з тим, що вивченням його персони займались Піфагор, Евклід, Архімед, тоді як інші трикутники були обділені увагою стародавніх учених.

Прямокутний трикутник: Тут з вами важко погодитися. У школі Піфагора займалися вивченням трикутників узагалі, а не тільки прямокутних. І теорема про суму кутів трикутників – це також теорема Піфагора, справедлива для будь – якого трикутника.

Гострокутний трикутник: А як прямокутний трикутник вихваляється своїми гострими кутами, надаючи їм запаморочливих властивостей! Він заявив, що тригонометрія виникла завдяки прямокутному трикутнику.

Прямокутний трикутник: Але це справді так. Згадаймо, що косинус, синус, тангенс гострих кутів визначається співвідношенням між своїми лінійними елементами.

Рівнобедрений трикутник: Як пишається прямокутний трикутник своїми пропорційними відрізками! Хоча моя висота опущена на основу, є і медіаною, і бісектрисою.

Прямокутний трикутник: Я не заперечую всіх заслуг вашої висоти, вельмишановний Рівнобедрений трикутнику, але я також пишаюся своєю висотою. Моя висота розбиває мене на два подібних мені трикутники, а сама є середньою пропорційною проекцій катетів на гіпотенузу.

Правильний трикутник: Шановні судді, ви все бачили й чули. Вам вирішувати долю хвалька.

Прямокутний трикутник: Я визнаю свою провину. Я, звичайно, неправий, що дозволяв собі таке зазнайство по відношенню до своїх братів – трикутників. Я такий самий, як і ви. У мене три сторони, три вершини, три кути. І я не винен у тому, що центр описаного кола у мене лежить на середині гіпотенузи. Але я не люблю ледарів і неуків. Я хочу, щоб школярі краще знали геометрію. Я віддаю себе у руки правосуддю за однієї умови: долю мою нехай вирішують ті, хто справді добре знайомі зі мною.

Учитель: Друзі! Я думаю, що всі ви розумієте важливість всіх трикутників, а не тільки прямокутних.

VІ. Різні доведення теореми Піфагора(метод проектів)

Слово вчителя:

Теорема Піфагора має багату історію. Ще задовго до Піфагора вона була відома єгиптянам, вавілонянам, китайцям та індійцям. Доведення самого Піфагора до нас не дійшло. В наш час є більше 100 різних доведень теореми Піфагора. Можливо, що одне з них належить Піфагору чи його учням.

Теорема Піфагора чудова тим, що вона зовсім не очевидна. Із простого споглядання прямокутного трикутника не зробиш висновок, що між його сторонами є таке просте співвідношення a² + b² = c². Але це співвідношення стає очевидним, якщо вдало побудувати малюнок.

1. Давньоіндійське доведення

У книзі „ Вінок знання” індійський математик Бхаскара наводить доведення теореми Піфагора у вигляді креслення з підписом „Дивись!” Як дістати з креслення Бхаскара доведення теореми Піфагора?

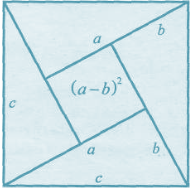
Площа квадрата, побудованого на гіпотенузі с трикутника, дорівнює сумі площ чотирьох прямокутних трикутників і квадрата, довжина сторони якого a – b. Тобто

c²= 4 · + ( а – b)² = 2 аb + а² - 2ab + b² = a² + b².

Отже, c² = a² + b².

2. Геометричне доведення:

Нехай у прямокутному трикутнику катети дорівнюють а і в, а гіпотенуза с.

Побудуємо два квадрати, сторони яких дорівнюють а+в.

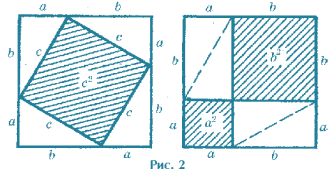
no24_02

Очевидно, що площі цих квадратів рівні. У першому квадраті виділимо квадрат, побудований на гіпотенузі (дістанемо квадрат і 4 рівні прямокутні трикутники); у другому квадраті виділимо квадрати, побудовані на катетах (дістанемо два квадрати і 4 рівні прямокутні трикутники). Виключаючи трикутники 1-4, бачимо, що: с²= а² + в²

Тепер неважко побачити, що площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах цього трикутника.

3. Наочне доведення теореми Піфагора.

VІІ. Первинне закріплення матеріалу.

Задачі за готовими рисунками.

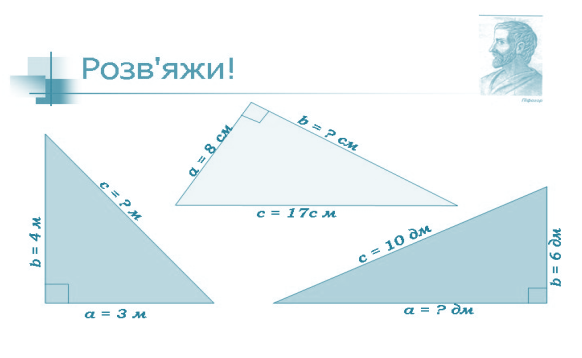
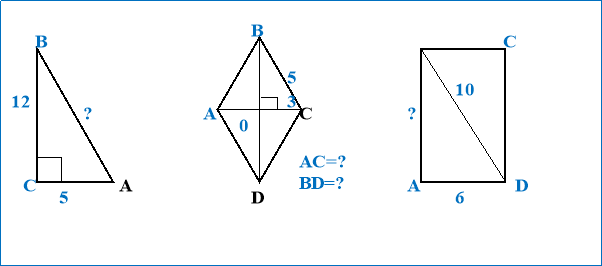
VІІІ.Змагання професіоналів «Магічний трикутник»

Робота в парах ( розв’язування задач практичного характеру )

Пара І

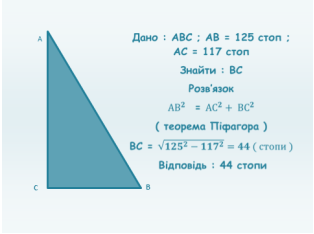
Старовинна задача

Сталося якомусь чоловіку до стіни драбину поставити , стіни ж тої висота є 117 стоп .І відати хоче він , на скільки стоп драбини нижній кінець від стіни отстояти має , якщо драбини довжина 125 стоп .

Пара ІІ

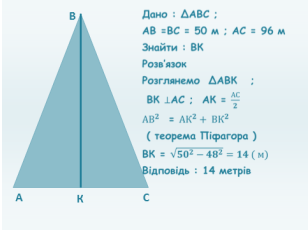
Дах будинку має форму рівнобедреного трикутника ( АВС) , АВ=50м ,основа трикутника АС = 96м . Знайти висоту даху

Пара ІІІ

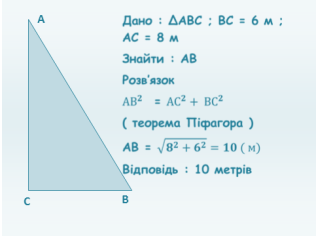
Висота новорічної ялинки 8 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АВ₁, АВ₂ однакової довжини і закріпили їх на підлозі на відстані 6 м від основи ялинки. Якої довжини повинна бути натягуюча проволока, щоб ялинка стояла вертикально.

Теорема Піфагора в літературі.

Теорема Піфагора є однією з основних у геометрії. За її допомогою можна вивести більшість теорем геометрії й розв’язувати безліч задач. Цій теоремі навіть присвячені вірші. (Учень читає вірш )

Про теорему Піфагора

Суть істини проста: вона – дороговказ,

Що сяє для людей, одвічна і сувора,

Тому, як в давнину, вражає нині нас

Беззаперечна теорема Піфагора.

За дотик мудрості уславлених богів,

Ковток із джерела незвіданого смаку,

Олімпу Піфагор тоді осанну звів

І сто биків заклав жертовних на подяку.

Відтоді всі бики, що чують серед нив,

Що людство прагне знов за обрії духовні,

Збентеженно ревуть, хоча і ясла повні,

Такий в них Піфагор навіки жах вселив.

Не зборе бик того, що істина зборола,

Тому вони й ревуть, схиливши очі долу.

ІХ. Рефлексія.

Метод «Квітка засвоєння».

Учні прикріплюють на дошці пелюстки квітки:

Зелені – все зрозуміло,

Сині – майже все зрозуміло,

Жовті – зрозуміло наполовину,

Оранжеві – дещо зрозуміло,

Червоні – нічого не зрозуміло. Х.Підсумок уроку

Сьогодні ви зробили ще один крок, щоб вважати себе людиною розумною... Навіть єгипетські жерці, віддаючи своїх дітей для навчання мистецтву, хотіли передусім, щоб вони вивчали геометрію. А Гіппократ вважав, що для того, щоб стати добрим лікарем і знати як розміщені органи, слід вивчати геометрію. Один із послідовників Сократа, опинившись на безлюдному острові та побачивши на піску накреслені геометричні фігури, радісно вигукнув: "Я бачу геометричні малюнки, отже, я бачу сліди людей розумних!" Недарма Паскаль сказав, що "серед рівних по розуму за однакових умов переважає той ,хто знає геометрію". Вам іти у світ, вам доводити ще не одну математичну і не одну життєву теорему. Можливо, з часом теорема Піфагора буде здаватися вам до сміху простою. Але сьогодні ви подолали певний рубіж, ви стали розумнішими на цілу теорему - на теорему Піфагора, цікаву, могутню і Вічну.Дякую вам за співпрацю. Ви всі були молодці, (оголошуються оцінки) ХІ.Домашнє завдання.

Скластим задачі практичного змісту, для розв’язання яких неохідно використати теорему Піфагора.

І , якщо залишається час , то

Гра «Вірю — не вірю».

Правила такі: якщо твердження здається вам правильним, то покажіть знак плюс, інакше — знак мінус.

Чи вірите ви, що:

1) будь-який прямокутний трикутник називається єгипетським; (Ні.)

2) Піфагор брав участь у кулачному бої на Олімпійських іграх; (Так, він був чемпіоном у цьому виді спорту.)

3) Фалес був уболівальником і помер на трибуні Олімпійського стадіону під час бою Піфагора; (Так.)

4) якщо кожного дня по 10 годин просто переписувати праці Леопарда Ейлера, то не вистачить і 76 років, щоб переписати їх; (Так, його праці надруковані у 75 великих томах.)

5) Шарль Перро, автор казки про дівчинку у червоному капелюшку, написав казку «Кохання циркуля і лінійки»; (Так.)

6) Наполеон Бонапарт писав математичні роботи; (Так, відома задача Наполеона.)

7) два в квадраті — 4, три в квадраті — 9, кут у квадраті 90; (Так.)

8) Піфагор першим розробив математичну теорію музики; (Так.)

Пифагор