Урок із теми "Теорема Піфагора - одна зі скарбів геометрії"

КОНСПЕКТ

Уроку-конкурсу з геометрії
у 8 класі.

ТЕМА УРОКУ: ТЕОРЕМА ПІФАГОРА - ОДНА ІЗ СКАРБІВ ГЕОМЕТРІЇ

ТИП УРОКУ: Узагальнення та систематизація знань і навичок.

МЕТА: ОСВІТНЯ: повторити, узагальнити й систематизувати

знання та вміння розв ’язувати задачі, використовуючи

теорему Піфагора і її наслідки.

РОЗВИВАЮЧА:  - розвивати вміння узагальнювати та систематизувати;

•     коректувати одержані знання.
•     привчати самостійно мислити, зв’язно висловлювати й правильно оформляти власні думки;
•     аналізувати й повторювати математичні факти

ВИХОВНА: - виховувати любов до математики;

•     культури математичного мовлення;
•     почуття дружби, взаємодопомоги;
•     дотримуватись етичних норм поведінки

ОБЛАДНАННЯ: - плакат з епіграфом:

•    плакат з кросвордом;
•    портрет Піфагора;
•    плакат з піфагорійською зіркою;
•    кольорова крейда;
•     плакат з розв’язаними завданнями.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ.

ВЧИТЕЛЬ: Теорема Піфагора — основа евклідової геометрії, тому її треба добре засвоїти. Сьогодні у нас урок однієї теореми, на якому ми підводимо підсумок вивченню цієї теми. У світі відомо понад сто різних доведень теореми. Можливо, і ви знайдете свій оригінальний спосіб доведення, тож хай вам щастить.

ТЕОРЕМИ ЕВКЛІДА І ПІФАГОРА ГЛИБОКО ВПЛИНУЛИ НА ХАРАКТЕР МИСЛЕННЯ НЕ ТІЛЬКИ МАТЕМАТИКІВ.

(Г. Харді)

II. КОНКУРС И:

ВЧИТЕЛЬ: Якщо ви відгадаєте кросворд то будете знати, як називалась теорема Піфагора у Древній Греції.

( Клас поділяється на три команди).

1.Кросворд.

Питання:

1.   Чотирикутник, у якого протилежні сторони паралельні.
2.    Древньогрецький вчений.
3.    Прямокутник, у якого всі сторони рівні.
4.    Чотирикутник, у якого тільки дві сторони паралельні.
5.    Паралелограм, у якого діагоналі рівні.
6.    Геометричне місце точок площини, рівновіддалених від даної точки.
7.    Паралелограм, у якого всі сторони рівні є...
8.    Центр кола, вписаного в трикутник, лежить на перетині...
9.    Твердження, які не доводяться називаються...

ПАРАЛЕЛОГРАМ

ФАЛЕС

КВАДРАТ

ТРАПЕЦІЯ

ПРЯМОКУТНИК

КОЛО

 РОМБ

БІСЕКТРИСА

АКСІОМА

ВЧИТЕЛЬ: Чому теорему називали гекатомбою?

УЧЕНЬ: Легенда розповідають, що коли Піфагор довів свою теорему, він віддячив богам, принісши їм у жертву сто биків.

2. Бліц-турнір

( Кожна команда отримує по 6 питань).

Питання 1 команди:

•    сторони, що утворюють прямий кут, називаються ...
•     квадрат гіпотенузи дорівнює ...
•     прямокутні трикутники рівні за...
•     радіус кола, описаного навколо прямокутного трикутника дорівнює
•     трикутник зі сторонами 3,4,5 називається ...
•     медіана прямокутного трикутника, проведена до гіпотенузи є ...

Питання 2 команди:

•     сторона, яка лежить напроти прямого кута називається...
•     сума гострих кутів прямокутного трикутника дорівнює ...
•         висота прямокутного трикутника, проведена з вершини прямого кута дорівнює...

•    центр описаного навколо прямокутного трикутника кола лежить на
•    трикутник зі сторонами 9,12,15 називається ...
•     площа квадрата, побудованого на гіпотенузі дорівнює ...

Питання 3 команди:

•     площа прямокутного трикутника дорівнює…
•     чому рівні гострі кути рівнобедреного прямокутного трикутника
•       сторона, що лежить в прямокутному трикутнику напроти кута в 30 градусів дорівнює…
•     гіпотенуза прямокутного трикутника, вписаного в коло є...
•     в прямокутному трикутнику будь-який з катетів ...
•     відношення протилежного катета до гіпотенузи називається...

ПІДСУМОК : перемагає та команда, яка набрала більшу кількість балів,

З. Математична естафета.

Конкурс між учнями трьох команд. Кожна пара учнів 1-ої парти розв’язує одну задачу і передає учням наступної парти і т.д. Потім взаємоперевірка. Ряди міняються завданнями на картці і всі разом перевіряють відповіді. На дошці плакат з цими розв'язаними завданнями.

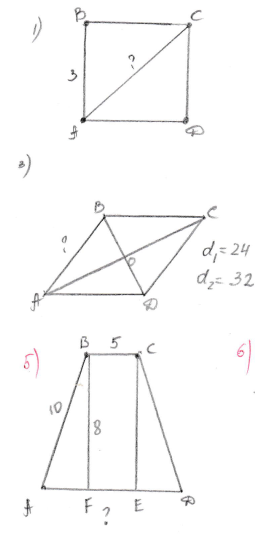
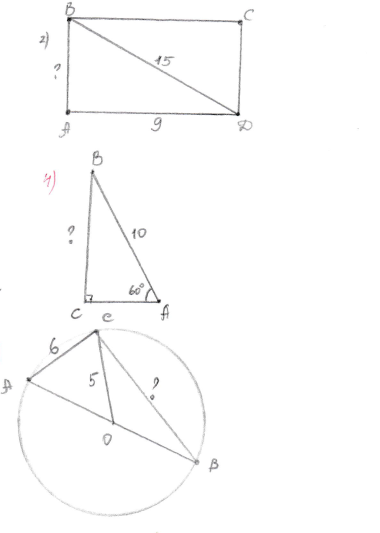
ПЛАКАТ-ВІДПОВІДЬ

1. AC = 9+9 = 3 2(см)
2. AB = 12 см
3. AO = 12 см, BO = 16 см, AB = 20 см
4. B = 30, AC = 5 см, BC = 75 = 5 3(см)
5. AF = 6 см, DE = 6 см, AD = 6+6+5 = 17 (см)
6. CO = AO = OB = 5 см, AB = 10 см, BC = 8 см

4. Історичний конкурс.

ВЧИТЕЛЬ: На уроках ми дуже часто звертались до теореми Піфагора. Що ви знаєте про цю людину, про її життєдіяльність? (Кожна команда одержує 4 питання).

Питання 1 команді:

•     піфагорійці надавали містичного значення числам. самою страшного клятвою у них вважалася клятва числом ... яким і чому? {Число 36, що має такі властивості : сума кубів трьох перших натуральних чисел дорівнює 36, 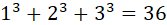; сума перших чотирьох парних і перших чотирьох непарних натуральних чисел дорівнює 36 (2+4+6+8)+(1+3+3+7)= 36 - на цьому був збудований весь світ — вважали піфагорійці).
•    Чим займалися піфагорійці крім математики? (Музикою, релігією, філософією).
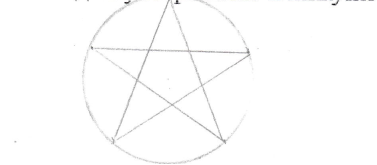
•     Щз було для піфагорійців священним знаком? (Піфагорійська зірка - пентаграма).
•     З якою метою використовували мотузку, поділену вузликами на 12 рівних частіш в Стародавньому Єгипті (Для- побудови прямого кута).

Питання 2 команди:

•    Які числа називають Піфагоровими? ( Трійка чисел, для яких виконується відношення).
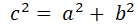•     Яке відкриття в школі Піфагора призвело до першої кризи в математиці? (Відкриття ірраціональних чисел).
•     Чому у Німеччині та Франції теорему Піфагора називали “ослячим мостом’? (Якщо учень  не  зумів  через  нього “перейти ”, то це був справжній осел).
•    Яку ще відому геометричну теорему приписують Піфагору? (Сума кутів трикутника дорівнює двом прямим кутам).

Питання 3 команди:

•    Назвіть древньогрецьких вчених-математиків. (Евклід, Піфагор, Фалес).
•     В яких країнах була відома залежність між сторонами прямокутного трикутника ще за 1000 років до Піфагора (Древньому Вавилоні та Єгипті).

•            Чому теорема Піфагора називалась гекатомбою. ( Приніс в жертву 100 биків).
•   З якого виду спорту Піфагор був олімпійським чемпіоном? ( З кулачного бою).

5. Творче завдання “Поміркуй”.

ВЧИТЕЛЬ: Теорема Піфагора чудова тим. що сама по собі вона зовсім не очевидна. Наприклад, властивості рівнобедреного трикутника можна бачити безпосередньо па малюнку. Проте скільки не дивись на прямокутний трикутник, ніяк не побачиш що між його сторонами є таке просте співвідношення: . Але це співвідношення стає очевидним , якщо вдало побудувати малюнок. В цьому є найкращій геометричний стиль: за допомогою дотепної побудови зробити неочевидне очевидним. В математичних трактатах Древньої Індії, доводячи теорему, часто наводили тільки малюнки. Супроводжувати його лиш одним словом “Дивись!”

•   Давайте і ми подивимось і доведемо теорему Піфагора

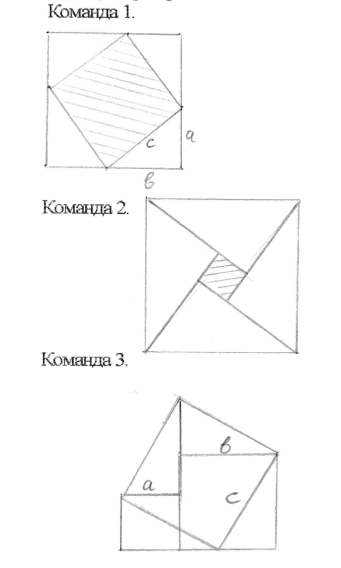
Кожна команда одержує малюнок, по якому вона повинна довести теорему Піфагора

6. Математична вікторина “ Хто перший?”

Задача 1. Назви всі трикутники, чотирикутники і п`ятикутнини, що входять у зображення п`ятикутної зірки

Задача 2. Розмістити п`ять відрізків так, щоб вони малт 10 крапок перетину.

Задача 3. На березі струмка, ширина якого 4 фута, росла тополя. Порив вітру зламав її на висоті 3 футів від землі так, що верхній кінець її торкнувся другого берега струмка. (Стовбур тополі напрямлений перпендикулярно до течії струмка). Визнати висоту тополі.

Задача 4. Дробину завдовжки 13 футів приставили до стіни на 5 футів. На скільки опуститься дробина на стіні, якщо іі основу відсунути ще на 7 футів

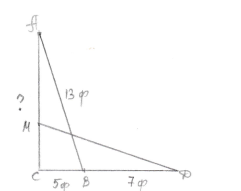Розв`язання:

AC = = 12(см)

MC =  = 5(см)

 AM = 12 –  5 = 7 (см)       

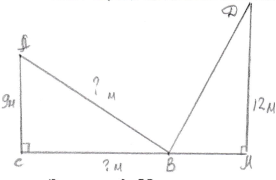
Розв`язання: ABC та DBM – подібні

до египетського, бо AB = BD,

а AC = 9 м, MD = 12 м, тоді BC = 12 м, BM = 9 м,

тобто CM = 12+9 = 21 (м), AB = 15 м

Задача 6. На запитання, скільки учнів навчається в школі, Піфагор відповів: ^“”Половина всіх учнів вивчає математику, чверть - музику, сьома частина - мовчить і, крім того, є іще три жінки ” .Скільки тоді було учнів у Піфагора?

Розв'язання: Нехай у Піфагора було х учнів, тоді х учнів вивчає математику, х учнів вивчає музику, х учнів мовчить і, крім того є ще три жінки. Складемо рівняння:

14 x + 7x+4x+28 = 28x

3x=84

X=28

Відповідь: 28 учнів

III. ПІДСУМОК УРОКУ.

Підводяться підсумки конкурсів, визначається переможець. Найактивніші учні отримують оцінки.

Вчитель дякує учням за участь у конкурсах, робить висновки, звертає увагу на ті моменти, де учні помилялися. Окремим учням вчитель пропонує ще раз проглянути той чи інший матеріал, інших хвалить за активність, хороші знання.