Урок "Квадратні рівняння"

 

 

 

 

 

 

 

 

 

 

 

 

Конспект уроку на тему:

 

 

 

 

 

 

 

 

 

 

 

 

Учитель математики                                                                                                   Ярова В. В.

 

 

 

 

Мета. Ввести поняття квадратного рівняння. Розробити алгоритм розв’язування квадратних рівнянь.

Спонукати учнів до самостійного творчого мислення.

Виховувати культуру математичного запису та графічних побудов.

Розвивати логічне мислення та культуру мовлення учнів.

Тип уроку: вивчення нового матеріалу

Обладнання:  комп’ютерна презентація з основними тезами до уроку.

Хід уроку.

І. Організаційний момент,

ІІ. Актуалізація опорних знань

Інтерактивний метод «Незакінчене речення».

1.Рівність із невідомим значенням змінної називається… (рівнянням).

2.Значення змінної, для якої рівняння перетворюється у правильну числову рівність називається…(коренем рівняння).

3.Розвязати рівняння означає …(знайти всі його корені або довести, що їх немає).

4.Опис якогось реального об’єкта чи процесу мовою математики називають …(математичною моделлю).

5.Математичною моделлю задачі є …(рівняння або система рівнянь).

6.Рівняння виду ах+b=0 називають…(лінійним).

 

ІІІ. Мотивація навчальної діяльності.

ІV. Вивчення нового матеріалу.

Введення поняття квадратного рівняння.

Квадратним вважають кожне рівняння, яке після розкриття дужок, перенесення всіх членів у ліву частину і зведення подібних членів набуває вигляду                 ,                                                                       (1)

де – довільні числа (а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член), х – змінна. (слайд 2)

Якщо а = 1, то квадратне рівняння (1) називається зведеним.

Класифікацію квадратних рівнянь можна зобразити такою схемою (див. схему 1): ( слайд 3)

 

 

 

 

 

 

 

 

 

 

 

 

 Способи розв’язування квадратних рівнянь.

 Існують різні способи розв’язування повних квадратних рівнянь. Розглянемо один із способів. (слайд 5)

       Застосування формули коренів квадратного рівняння.

Учитель. Обчислюють значення виразу . Його називають дискримінантом (лат. Diskriminans - розрізняючий) даного квадратного рівняння і позначають буквою D.

Потім знаходять корені рівняння за формулами:

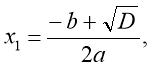
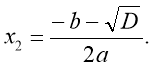
Це формула коренів квадратного рівняння. Користуючись нею, можна розв’язати будь-яке квадратне рівняння.

 

V. Формування вмінь

1	6х²  – х  + 4  = 0	а = 6,	в = -1,	с = 4
2	12х  -  х² +  7  =0	а = -1,	в = 12,	с = 7
3	8 + 5х² = 0	а = 5,	в = 0,	с = 8
4	х – 6х² = 0,	а = -6,	в = 1,	с = 0
5	- х + х² = 15	а = 1,	в = -1,	с = -15

1. Виконання усних вправ

Вкажіть коефіцієнти квадратного рівняння (слайд 4)

 

2. Виконання письмових вправ

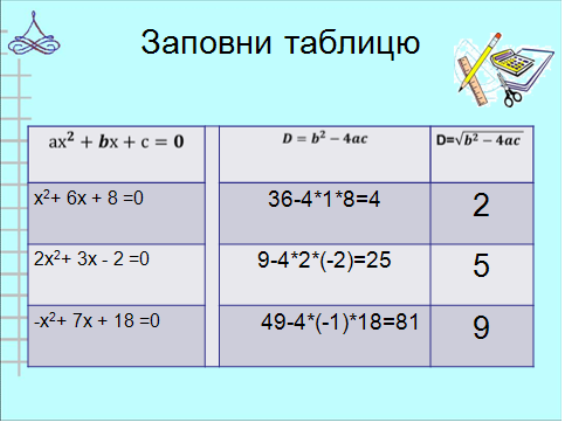
1) Для квадратного рiвняння знайдiть дискримiнант ( слайд 6)

x2+ 6x + 8 =0	36-4*1*8=4	2
2x2+ 3x - 2 =0	9-4*2*(-2)=25	5
-x2+ 7x + 18 =0	49-4*(-1)*18=81	9

 

2) Розв’яжи  квадратне рiвняння за формулою.  (слайд 7)

1) 3х² + 4х + 1 = 0,   2) 5х² - 4х – 9 = 0,  3)  6х² + 37х + 6 = 0,

4) 7х² + 2х – 5 = 0,    5) 13х² - 18х + 5 = 0,  6) 5х² + х – 6 = 0.

VІ. Підведення підсумків уроку.

1) Як же встановити, чи має квадратне рівняння корені і скільки?

Треба знайти дискримінант і порівняти його з нулем. Якщо більше від нуля, то рівняння має два різних корені, якщо дорівнює нулю – два корені, що збігаються, якщо менше нуля – рівняння дійсних коренів не має.

2) В якому випадку правильно знайдено дискримінант?

а)

б)

в)

г)

 

VІІ.  Домашнє завдання:

Вивчити - § 39, 40. Виконати  № 292;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Слайд 1

 

 

Слайд 2

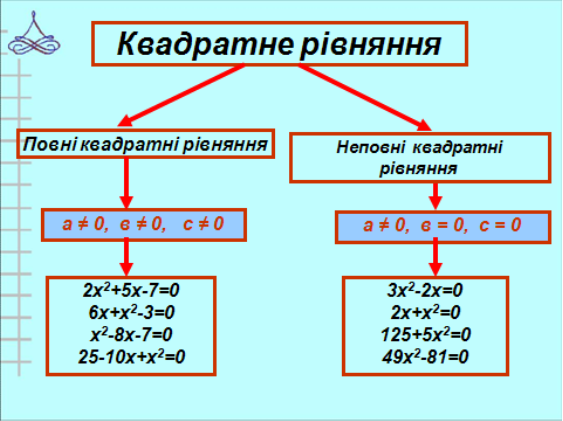
Слайд 3

 

 

Слайд 4 

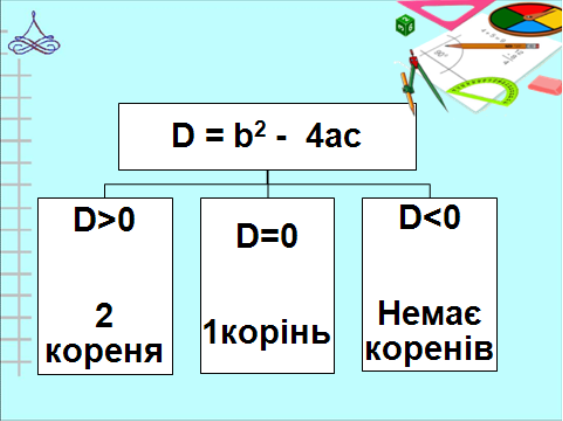
Слайд 5

 

 

        Слайд 6

Слайд 7

 

 

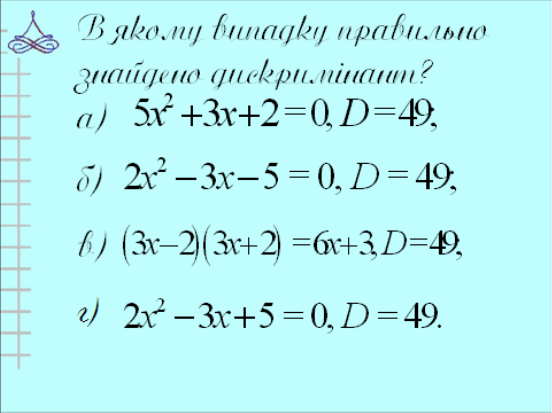
Слайд 8