урок. Лекція № 5 Тема: Площина і пряма у просторі.

Лекція № 5

Тема: Площина і пряма у просторі.

1.Різні види рівнянь площини.

2.Різні види рівнянь прямої у просторі.

3.Кут між двома прямими. Взаємне розміщення двох прямих у просторі.

4.Відстань від точки до прямої.

5.Взаємне розміщення прямої і площини у просторі.

1.Різні види рівнянь площини.

Загальне рівняння площини в тривимірному просторі, яка проходить через точку (x₀;y₀;z₀) перпендикулярно до вектора    має вигляд

                       A(x-x₀)+B(y-y₀)+C(z-z₀)                                              (1)

або

                          Ax+By+Cz=0                                                            (3)

Спеціальними площинами є площини OXY (рівняння z=0), OXZ (рівняння  y=0) та OYZ (рівняння x=0).

Рівняння площини, яка проходить через три задані точки  (x₀;y₀;z₀), (x₁;y₁;z₁), (x₂;y₂;z₂) (якщо ці точки не лежать на одній прямій), є таким:

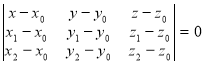                                                         (4)

Приклад.  Записати рівняння площини, яка проходить через точки  M₀(1;2;3), M₁(2;1;2) та M₃(3;3;1).

Маємо             ,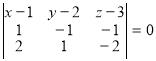

 звідки   x+4y-4=0.

Рівняння площини у відрізках є таким:

                       .                                                             (5)

Ця площина проходить через точки  (a;0;0), (o;b;0) та  (0;0;c).

Приклад.  Ціни за одиницю кожного з трьох товарів становлять, відповідно, 2, 3 та 4 умовні одиниці. Бюджет споживача дорівнює 120 умовних одиниць. Зобразити графічно бюджетне обмеження цього споживача.

Нехай споживач на всі гроші купив x одиниць першого товару, y одиниць другого та z одиниць третього. Тоді виконується рівність

                                   2x+3y+4z=120.

Ми отримали бюджетне обмеження споживача як загальне рівняння площини.

Зручніше записати це обмеження у вигляді рівняння площини у відрізках (виконавши ділення на 120):

                                    .

`Отже, споживач може купити або тільки 60 одиниць першого товару, або тільки 40 другого, або тільки 30 третього, а також може перебувати в довільній іншій точці площин     за умов x0; y0; z0 (рис .1).

                                                 z

                                                                                 Бюджетне обмеження –

                                                                             частина площини в просторі

                                               30

                                                             40                    

                                                                                             y

                                    60

                                 x

                                             Рис. 1.

Якщо ж витрачають не всі гроші, то бюджетне обмеження буде тетраедром:

                         .

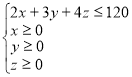Розглянемо випадок, коли споживач зовсім не купує третього товару (z =0). Тоді бюджетне обмеження представлятиме собою відрізок прямої на площині

                       ,

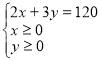або множину точок всередині трикутника (рис. 2)

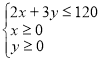
 .                                  у    

                                                                      Бюджетне обмеження -

                             40                                     відрізок прямої на площині

                                                                60              x

                                        Рис. 2.

2.Різні види рівнянь прямої у просторі.

Рівняння прямої у тривимірному просторі також записується багатьма способами.

Пряму як перетин двох площин задають системою лінійних рівнянь

                  .                                                      (6)

Симетричне (канонічне) рівняння прямої, що проходить через точку  (x₀;y₀;z₀)  паралельно до напрямного вектора  , має вигляд

                      .                                                 (7)

Параметричне рівняння прямої є таким:

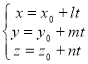                             .                                                          (8)

Рівняння прямої в просторі, яка проходить через дві точки (x₁;y₁;z₁)  та  (x₂;y₂;z₂) , є подібним до рівняння прямої на площині:

                    .                                                (9)

Приклад.  Пряма в просторі проходить через дві точки: M₁(1;2;3) та  M₂(4;6;8) .  Рівнянням цієї прямої згідно (9) є рівняння

                        .

Виконавши операції віднімання, отримуємо канонічне рівняння

                   .

Від останнього рівняння перейдемо до параметричного задання прямої (формула 8):         .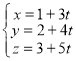

3.Кут між двома прямими. Взаємне розміщення двох прямих у просторі.

Для знаходження кута між двома прямими

і

візьмемо до уваги, що вектори і колінеарні відповідним прямим і скористаємося формулою:

.

З останньої формули випливає умова перпендикулярності двох прямих

,

а умову паралельності двох прямих дістанемо як умову колінеарності напрямних векторів і :

.

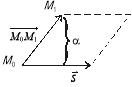
4.Відстань від точки до прямої.

Розглянемо ще задачу знаходження відстані від точки до прямої .

Шукану відстань можна розглянути як довжину висоти паралелограма, побудованого на векторах і (рис. 3). Відомо, що площа паралелограма дорівнює модулю векторного добутку векторів, на яких побудовано цей паралелограм. Доходимо висновку, що шукану висоту, а отже, і відстань від точки до прямої можна знайти за формулою:

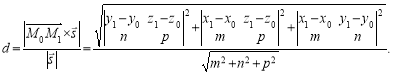
5. Взаємне розміщення прямої і площини у просторі. 

Нехай задано пряму і площину у просторі. Якщо

,

то пряма перпендикулярна до площини, а коли

,

пряма паралельна площині.

Нехай . Знайдемо координати точки перетину площини і прямої. Перейдемо до канонічного рівняння прямої

Знайдемо кут між площиною і прямою.

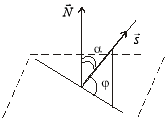
Кут  між площиною і прямою дорівнює куту між прямою і її проекцією на площину (рис. 4). Вектор — перпендикулярний до площини, а кут , який він утворює з вектором , разом з  у сумі дорівнює 90. Тобто  +  = 90.

Знайдемо кут  як кут між двома векторами.

.

Якщо , то , а якщо , то , у будь-якому разі . Отже,

.