Тема уроку:  Логарифм числа. Основна логарифмічна тотожність.

 

Мета уроку: Ввести поняття логарифма числа, основну      

                       логарифмічну тотожність. Формувати вміння

                       розв’язувати основні задачі на знаходження числа N

                       за його логарифмом х і основою а;

                       знаходження основи а за даним числом N і його

                       логарифмом х ; логарифма х даного числа N за даною

                       основою а; застосовувати основну логарифмічну

                       тотожність до розв’язування вправ.

 

 

 

 

№ п/п	Етапи уроку	Час проведення	Прийоми проведення
І	Організаційний момент	3 хв.	“Прийом рамки”
ІІ	Мотивація навчальної діяльності	3 хв.	Практичність теорії
ІІІ	Актуалізація опорних знань	3 хв.	Проблемний підхід
ІV	Вивчення нового матеріалу	15 хв.	Бесіда
V	Первинне застосування знань	16 хв.	Робота біля дошки “Поясни”. Робота в парах “Віднови хід думок”
VI	Рефлексія	3 хв.	“Напиши”
VII	Д/З Підведення підсумків	2 хв.	Завдання “масивом” “Прийом рамки”

 

Очікувані результати: Вміння використовувати означення логарифма на продуктивно – операційному рівні.

 

 

 

Учні повинні :

Знати:

• Означення логарифма;
• Десяткові і натуральні логарифми;
• Основну логарифмічну тотожність.

Уміти:

• Розв’язувати  основні задачі на використання означення логарифма.

 

                                          Хід уроку:

І. Організаційний момент.

Понад 2400 років тому китайський мислитель і філософ Конфуцій сказав:

Те, що я чую, я забуваю.

Те, що я бачу й чую, я трохи пам’ятаю.

Те, що я чую, бачу й обговорюю, я починаю розуміти

Коли я чую, бачу, обговорюю і роблю, я набуваю знань і навичок.

Я закликаю вас до співпраці. Будьте уважні протягом уроку. Думайте, запитуйте, записуйте – бо шляхом до істини нам з вами йти разом.

  Повідомлення теми, мети та очікуваних результатів уроку.

ІІ. Мотивація навчальної діяльності.

  Винайденню логарифмів значною мірою сприяли потреби удосконалення обчислень. Наука про логарифми виникла на початку 17 ст. Мореплавці того часу змушені були виконувати дуже громіздкі обчислення, щоб визначити курс і знаходження корабля у відкритому морі, астрономи – щоб обробити результати спостереження за рухом планет. Я сподіваюсь, що серед вас є майбутні астрономи і капітани кораблів, отже знання отримані сьогодні стануть в пригоді.

ІІІ. Актуалізація опорних знань учнів.

• Що ми називаємо рівнянням?
• Що означає розв’язати рівняння?
• Що ми називаємо розв’язком рівняння?

Розв’язати рівняння:

а) 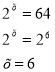 б)                         

 

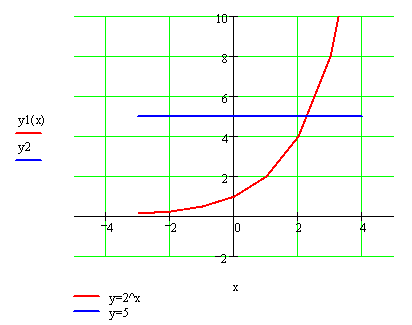
Рівняння б) має розв’язок, давайте з’ясуємо чому?

Розв’яжемо його графічним способом. Графіком функції

є експонента, а графіком є пряма,  паралельна

осі ОХ. Графіки перетинаються  в одній точці, отже рівняння

має один розв’язок.

 Що це за розв’язок? Як його знайти? Яке це число?

 

Сьогодні на уроці ми маємо знайти відповіді

 на ці запитання. Для цього нам потрібно ввести

нове поняття, за допомогою якого ми зможемо

розв’язувати рівняння такого типу.

 

 

IV. Пояснення нового матеріалу.

           а – основа степеня,      a>0, a1

                      х – показник степеня

                      N – число N>0

                      N0 , рівняння коренів немає.

 

Корінь рівняння називають логарифмом числа N за основою а.

 

Означення: Логарифмом числа N за основою а (a>0, a1)  називається показник степеня х, до якого треба піднести а, щоб дістати число N.

 

Позначення:       

 

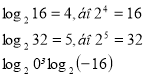
не мають змісту, бо рівняння 2^х=0 і 2^х=-16 не мають розв’язків.

 

Десяткові логарифми – це логарифми за основою 10.

Наприклад:

 

Натуральні логарифми    В математичних дослідженнях використовують логарифми за основою, вираженою ірраціональним числом, наближене значення якого дорівнює 2,718281828....2,718.

Леонард Ейлер запропонував позначити це число літерою е, його називають неперовим числом  на честь шотландського математика Джона Непера (1550-1617).   Логарифми з основою е називають натуральними, або непаровими і позначають

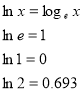
  З інформаційної теки історична довідка:

  Винайшли логарифми і майже одночасно почали їх застосовувати шотландський математик Джон Непер (1550-1617) і швейцарський математик, астроном і механік  Йост Бюргі (1552-1632). Проте перший крок до спрощення обчислень зробив німецький математик  Міхаель Штіфель (1487-1567), у якого поняття логарифма з’явилося в результаті зіставлення геометричної і арифметичної прогресій. Ця ідея бере свій початок у працях Архімеда (бл. 287-212 до н.е.)

   Розглянемо цю ідею на такому прикладі. Складаємо таблицю.

 

 

 

1	2	3	4	5	6	7	8	9	10
2	4	8	16	32	64	128	256	512	1024

 

  У верхньому рядку маємо арифметичну прогресію з різницею, що дорівнює 1, а в нижньому рядку – відповідно геометричну прогресію зі знаменником 2. Зіставивши числа у відповідних колонках, помічаємо, що в першому рядку ми маємо логарифми чисел другого рядка за основою 2. Так, наприклад,

.

 

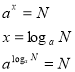
Основна логарифмічна тотожність.

Наприклад:

 

V. Первинне застосування знань.

Тисячі шляхів ведуть до помилки, до істини – тільки один.

 Наше завдання знайти цей єдиний правильний шлях.

Означення логарифма поєднує три величини, тому можна розглядати три види задач.

1. Знайти х, якщо відомі а і N.

Перший приклад пояснює вчитель, другий – на дошці колективно, наступні три -  учні біля дошки пояснюють. (заздалегідь підготувати картки). Учні біля дошки висловлюють свої міркування з приводу розв’язання того чи іншого прикладу.

Приклади:

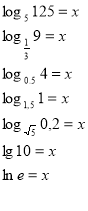
2. Знайти N, якщо відомі а і х

 

 

 

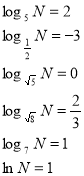
3. Знайти а, якщо відомі N і х.

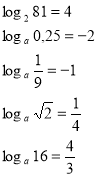
4. Обчислити, використовуючи основну логарифмічну тотожність.

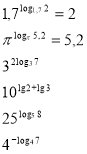
Робота в парах “Віднови хід думок”

2 учні , які сидять поруч  за партою отримують завдання-питання, на яке відповідають після обговорення (30 сек.), якщо пара не знає відповідь на своє запитання, просить допомоги класу.

Питання, які пропонуються учням:

1.З якими новими поняттями ви познайомилися сьогодні на уроці?

2. Скільки коренів має рівняння а^х=N  ? Як називають корінь рівняння?

3.Чи має зміст вираз     . Чому?

4.Продовжте думку: “Логарифмом числа N за основою а називається...”

5. Як можна записати у вигляді логарифмічних рівностей:

2⁷=128      5^-3=        216=6

6.Як перевірити чи правильно ви обчислили логарифм ?

7. За означенням логарифма, перевірити справедливість таких рівностей

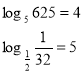
8. За означенням логарифма, визначити, яке число має логарифм 3 за основою 7.

9. За якою основою логарифм числа 10000 дорівнює 4?

10. Хто винайшов логарифм і вперше почав його використовувати?

11. Який логарифм називається десятковим?

12. Який логарифм називається натуральним?

13. В чому полягає основна логарифмічна тотожність?

14. Які основні задачі на використання означення логарифма ви знаєте?

 

 

  Оцінюються найкращі відповіді , протягом уроку (правильність, чіткість у формулюванні, розуміння сказаного)

 

VI Рефлексія.

Учні пишуть на заздалегідь заготовлених аркушах паперу речення, що починаються словами:

“Я знаю...

“Я вмію...

“Я можу...

І наклеюємо на плакат, який зроблено у вигляді сходинок, кожна сходинка підписана такими ж словами.

 

VII.  Домашнє завдання: підручник М. І. Шкіль, З. І. Слєпкань,

 О.С. Дубинчук “Алгебра і початки аналізу”10 клас  ст. 214-218 , запитання1-5  Завдання “масивом” вправи 1-20

 

Підведення підсумків.

  Філософ і мислитель Конфуцій говорив:

“ Три шляхи ведуть до знань:  шлях роздумів – це шлях 

найблагородніший , шлях наслідування – найлегший і шлях дослідження – найскладніший.”

    Подумайте над цими словами і виберіть свій шлях – шлях, який би поєднав в собі і роздуми, і дослідження, і наслідування, який приведе вас до вершини пізнання теми : “Логарифмічна функція”. Бажаю всім успіху. Дякую за урок.

 

 

 

 

   

Використана література:

1. Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. Навч. Закладів /М.І.Шкіль, З.І. Слєпкань, О.С.Дубинчук. – К.: Зодіак – ЕКО, 2002 – 272 с.
2. Прийоми педагогічної техніки. /А.Гін – Луганськ, 2005 – 84 с.
3. Освітні технології.: Навч.-метод.посіб./О.М.Пєхота та ін.. – К.:А.С.К.,2002. – 255с.
4. Настільна книга педагога. Упорядники: Андрєєва В.М.,Григораш В.В. – Х.: Вид. група «Основа», 2009. -352 с.