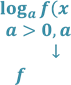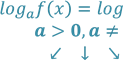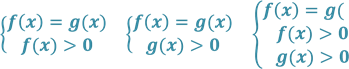ТЕМА: Логарифмічні рівняння.

МЕТА: Домогтися засвоєння студентами знань про вид найпростіших логарифмічних рівнянь та схеми їх розв’язування. Формувати вміння розв’язувати найпростіші логарифмічні рівняння. Виховувати вміння прогнозувати. Розвивати увагу, пам’ять, логічне мислення.

 

Структура заняття

1.     Перевірка домашнього завдання.

2.     Актуалізація опорних знань.

3.     Мотивація навчання.

4.     Логарифмічні рівняння.

5.     Розв’язування вправ.

6.     Домашнє завдання.

7.     Підсумок уроку.

 

Хід заняття

 

1.   Перевірка домашнього завдання

 

Опитування біля дошки.

Додаткове завдання

                  Знайти область визначення функції: а) log ₁₀ 6 _{ }x            x²  ; б) log x² _ 2 _{х } 3_ .

 

2.   Актуалізація опорних знань

 

Інтерактивна гра «Закінчіть речення»

1.       Областю визначення функції  є...

2.       Областю значень логарифмічної функції  є...

3.       Для функції  при , якщо   , то...

4.       Для функції  при , якщо  < , то...

5.       Якщо , то  ...

6.       Якщо , то  ...

7.       Якщо  і , то x...

8.       Якщо  і , то x...

9.       Якщо  і , то x...

10.   Якщо  і , то x...

 

3.   Мотивація навчання

 

Від XVII ст. і до появи мікрокалькуляторів і комп’ютерів наприкінці XX ст. основними засобами приблизних обчислень були таблиці логарифмів і логарифмічна лінійка. Сьогодні ми з’ясуємо, як, знаючи значення логарифма, знайти число, від якого береться логарифм, тобто вчитимемося розв’язувати логарифмічні рівняння.

           

                                                                                                                                     2

4.   Логарифмічні рівняння

 

Логарифмічними називають рівняння, які містять невідому під знаком логарифма.

Приклад,  log5  2 х  2 ; lg х  lg 11  lg 19  lg(30  х ) .

До найпростіших логарифмічних рівнянь відносять рівняння вигляду  та .

 

У більшості випадків найпростіші логарифмічні рівняння виду , де , , розв’язують на основі визначення логарифма, а рівняння виду

 – методом потенціювання.

 

Схема виконання рівносильних перетворень найпростіших логарифмічних рівнянь
Оскільки , то  і тому ОДЗ початкового рівняння враховано автоматично.

 

Приклад. Розв’язати рівняння:

 

.                                     2. .

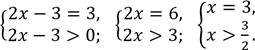Розв’язання:    Розв’язання:  , .

       Відповідь: .                                                                                         

Відповідь: .

Оскільки студентам важко дається урахування ОДЗ при розв’язуванні найпростіших логарифмічних рівнянь, то можливо запропонувати їм робити перевірку.

 

3. .

Розв’язання: , .

Перевірка: при , маємо: ; ; .

Відповідь: .

4.    .

Розв’язання: якщо логарифми двох чисел за однією й тією самою основою рівні, то рівні і самі числа, отже: ; ; .

Перевірка: при , маємо:

;  .

Цей вираз не має змісту, отже дане рівняння не має коренів.

Відповідь: .

                                                                                                                                     3

5.   Розв’язування вправ

 

Колективне розв’язування вправ підручника Істер О.С. Математика (алгебра і початки аналізу та геометрія, рівень стандарту): підруч. для 11-го кл. закл. заг. сер. освіти / О.С. Істер – Київ: Генеза, 2018. – 384 с.: іл. - 6.1, 6.3, 6.5, 6.7.

 

  

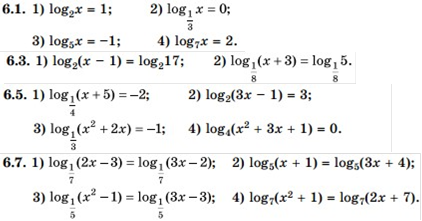
6.   Домашнє завдання

 

Розв’язати завдання підручника Істер О.С. Математика (алгебра і початки аналізу та геометрія, рівень стандарту): підруч. для 11-го кл. закл. заг. сер.

освіти / О.С. Істер – Київ: Генеза, 2018. – 384 с.: іл. - – 6.2, 6.6, 6.8(2, 3).

 

7.   Підсумок уроку

 

Фронтальна бесіда за технологією «Мікрофон»

1.   Які рівняння називають логарифмічними?

2.   Якими є особливості розв’язання логарифмічних рівнянь?

3.   Які властивості логарифма використовують під час розв’язування логарифмічних рівнянь?

4.   Про які способи розв’язування логарифмічних рівнянь ви дізналися на занятті?

5.   Що є причиною появи стороннього кореня в ході розв’язування логарифмічних рівнянь?