Урок математики в 6 класі з теми "Довжина кола. Площа круга"
Конспект уроку математики в 6 класі з теми «Довжина кола. Площа круга».
Формування компетентностей:
предметна компетентність : розглянути залежність між діаметром кола та його довжиною; ввести поняття про число П ; ознайомити учнів з формулами для обчислення довжини кола і площі круга; сформувати вміння застосовувати ці формули до розв’язування задач;
ключові компетентності :
математична компетентність – оперувати числовою інформацією, геометричними об’єктами на площині;
спілкування державною мовою - чітко , лаконічно та зрозуміло формулювати думку; розуміти , пояснювати і перетворювати тексти математичних задач;
спілкування іноземною мовою - спілкуватися англійською мовою з використанням математичних понять , вміння записати математичні терміни англійською мовою.
Тип уроку : засвоєння нових знань і вмінь .
Хід уроку
І. Мотиваційний етап.
Доброго дня всім! Рада вас бачити! Чи готові всі до уроку?
Одним із домашніх завдань було знайти , як читаються деякі математичні терміни англійською мовою. Тому відповідаючи на мої запитання прошу назвати ці терміни українською мовою і англійською та записати на дошці по- англійськи.
На минулому уроці ми з вами розглянули геометричні фігури, для побудови яких потрібен спеціальний прилад. Як називається цей прилад ?
( циркуль , compasses )
Які фігури можна накреслити за допомогою циркуля ?
( коло , circle і круг , round )
Чи вірно ,що одну й ту саму фігуру можна називати колом або кругом ?
(ні , бо коло – це лінія ,а круг – частина площини )
Як називають точку , відстань до якої від усіх точок кола однакова ?
( центр , centre )
Як називають відрізок , який сполучає центр кола з будь- якою точкою цього кола ?
(радіус , radius )
Як називають хорду , що проходить через центр кола ?
(діаметр , diameter )
Як називають частини , на які дві точки поділяють коло?
(дуга , arc )
Як називають частини , на які два радіуси поділяють круг ?
(сектор , sector )
ІІ. Цілевизначення і планування.
У 5 класі ми з вами готували виставу «Геометричний з'їзд». Зараз я б хотіла нагадати вам уривок з цієї вистави. Допоможуть мені в цьому Оксана і Максим, які виконають ролі Кола і Кулі. ( додаток 1 )
Подякуємо Оксані і Максиму, а я хочу звернути вашу увагу на відношення, про яке йшлося у виставі. Це відношення довжини кола до його діаметра. Виконуючи домашнє завдання, ви, мабудь, помітили, що якщо збільшити радіус, то і сама лінія кола теж буде довшою. Пропоную зараз обчислити це відношення.
Клас ділиться на три групи. Кожна група одержує інструкцію ( додаток 2 ), комп'ютерний диск і мірну стрічку . Хочу попередити , що результат може бути нескінченним десятковим дробом.( Групова робота учнів )
Заслуховуємо представників команд. ( 37 см : 11,5 см = 3,16 )
Зазначимо, що для всіх випадків відношення довжини кола до довжини діаметра є тим самим числом. Це число особливе і має спеціальну назву – число «пі». Повідомлення про це число підготував Павло. Надамо йому слово
( додаток 3 ).
Запишіть в зошити і будемо використовувати при обчисленнях : П= 3,14.
Діти, як ви думаєте,чи має практичне застосування спосіб , яким ви вимірювали довжину кола? ( Міркування учнів )
Отже, існує інший спосіб , за яким ми зможемо це зробити. Ви знаєте, що в математиці залежності між величинами виражають формулами. Сьогодні на уроці ми дізнаємося про формули 1) – для обчислення довжини кола, 2) – для обчислення площі круга, 3) – навчимося застосовувати ці формули до розв’язування задач.
Ви побачите, що є дуже багато задач, взятих із життя, які потребують знання цих формул.
ІІІ. Опрацювання навчального матеріалу.
Для виконання першого пункту нашого плану повернемося до відношення, яке ви одержали в групах, а саме l : d =П. Як з цього відношення знайти величину l ?
Запишемо формулу на дошці: l= П d. Яку величину треба знати, щоб обчислити довжину кола?
Обчисліть довжину кола, якщо його діаметр дорівнює 5 см. ( 15,7 см )
А чи можна обчислити довжину кола за відомим радіусом?( Міркування учнів )
Дійсно, d = 2 r , тоді l = 2 П r . Запишемо в зошити ще одну формулу.
Дуже багато задач легко розв’язати за формулою довжини кола . Ось, наприклад.
Задача 1. Криниця має коловорот із валом діаметром 0,25 м. Щоб витягнути за його допомогою відро з криниці , необхідно зробити 10 обертів. Яка глибина криниці?
l= П d = 3,14*0,25 = 0,785 ( м ) – довжина кола коловорота
0,785* 10 = 7,85 (м) - глибина криниці.
Якщо вас запитають яка глибина в метрах ? Що треба зробити?
Задача 2. Мавпеня пробігло три кола цирковою ареною . Яку відстань пробігло мавпеня? Відомо, що радіус циркової арени 4 м.
l = 2 П r =2*3,14*4 =25,12 (м) – довжина кола циркової арени.
25,12*3 = 75,36 (м) – пробігло мавпеня.
На подвір’ї нашої школи ростуть великі дерева. Чи можна виміряти діаметр стовбура дерева , не зрізаючи його ? ( Міркування учнів )
Задача 3. У Каліфорнії росте гігантська секвоя «Генерал Шерман». Її висота дорівнює 83,8 м, а довжина кола стовбура біля основи становить 34,9 м . Вік дерева налічує 2500 років. Це дерево вважають найбільшим живим організмом на Землі. Чому дорівнює діаметр стовбура цієї секвої біля основи ? (Для обчислення використаємо калькулятори та округлимо результат до одиниць )
d = l : П = 34,9 : 3,14 = 11 (м) –довжина діаметра . Це більше, ніж довжина нашого класу.
Фізкультхвилинка. ( додаток 4 )
Отже, які формули ми з вами вже вивчили? Що можна обчислити за цими формулами? (Відповіді учнів ).
А яку формулу ми ще планували вивчити на цьому уроці? Правильно, формулу для обчислення площі круга. Кожна група має на парті круг з лимона. Розділимо цей круг надвоє і розрівняємо шматочки. Перед вами два відрізки з трикутними зубчиками. Накладемо ці шматочки , щоб у нас утворився прямокутник. Довжина прямокутника П r, бо це довжина півкола , а ширина дорівнює радіусу кола. Чи вірно, що площа круга дорівнює площі утвореного прямокутника ?
Тільки обчислювати площу круга ми ще не вміємо , але знаємо, як обчислити плошу прямокутника. Як ? (Відповіді учнів ).
Вірно ! Треба помножити довжину прямокутника на його ширину . Тобто, площа круга S = П r * r , або простіше S = П r2.
Ми з вами вивели формулу для обчислення площі круга. В 9 класі ви дізнаєтеся про складне математичне доведення цієї формули, а поки що запишіть її в зошит і запам’ятайте.
А зараз попробуємо використати одержану формулу для розв’язування задачі
№ 739 з вашого підручника. Як можна обчислити площу кільця? (Відповіді учнів ). А які вимірювання слід зробити? (Відповіді учнів ). Для обчислень використаєм калькулятори.
S = 3,14 * 1,52 = 7,065 (см2 ) – площа більшого круга.
S = 3,14 * 0,52 = 0,785 ( см2 ) – площа меншого круга.
7,065 - 0,785 = 6,28 ( см2 ) - площа кільця.
Математичні знання допомагають вирішити різноманітні життєві завдання. Ось така ситуація. Дівчатка 6 класу вирішили на подвір’ї школи розбити клумбу круглої форми. Скільки насіння їм потрібно закупити , якщо на один квадратний метр землі потрібно 20г насіння? Чи достатньо числових даних в умові задачі?
Порадьте дівчаткам , як практично на місцевості розбити круглу клумбу. Радіус клумби 2м.
3,14*22 = 12,56 ( м2 ) – площа клумби.
12,56 * 20 = 251,2 ( г ) – насіння потрібно , щоб засіяти клумбу.
ІV. Рефлексивно – оцінювальний етап.
Отже, давайте проаналізуємо свою роботу на уроці, прослухавши притчу :
« Йшов мудрець, а на зустріч йому три людини, які везли під пекучим сонцем візки з камінням для будівництва. Мудрець зупинився і спитав кожного : «Що ти робив цілий день?». Перший похмуро відповів, що цілий день возив кляті камені. Другий відповів: «Я сумлінно виконував свою роботу». А третій посміхнувся, його обличчя засвітилося радістю і задоволенням: «А я брав участь у будівництві Храму!».
А що ж на уроці робили ви? Пропоную дізнатися про це за допомогою вправи «Незакінчене речення» , тобто я починаю речення , а ви закінчуєте.
- «На сьогоднішньому уроці ми дізналися….».
- «Найбільше мені сподобалось….».
- «Найважливішим відкриттям для мене було….».
- «Я тепер знаю такі формули….».
- «Свої знання я можу застосувати для ….».
V. Домашнє завдання. (За підручником «Математика. 6 клас» . Автори А.Г.Мерзляк, В.Б.Полонський, М.С.Якір )
Пункт 25, опрацювати, вивчити формули,
№ 732, 734, 745, або № 749 , 752 (для сильніших учнів )
Додаткове завдання. Скільки квадратних метрів тканини потрібно взяти, щоб пошити спідничку типу «сонце» для дівчинки з обхватом талії 45 см? Бажана довжина спіднички 30 см.
Для розв’язання цієї задачі потрібно знати , який крій має спідничка. Попробуйте самостійно знайти цю інформацію.
ДОДАТКИ
Додаток 1. ( уривок з вистави «Геометричний з’їзд» )
Коло: Я – Коло. Я у собі цікаву точку маю…
Куля: А хто ж він є, цей пункт, питаю?
Коло: Зветься центром він, від точок всіх моїх на рівній відстані один.
Куля: То ти – це замкнена крива?
Коло: Виходить так, шановна, суцільна й замкнена,
Тому із давнини охоплюю частину площини.
Куля : Які стосунки маєш ти з прямою?
Коло: А це залежно вже з якою.
Куля: Припустимо, якщо з тобою пряма в двох точках перетнеться?
Коло: В середині моїй її відрізок хордою всі звуть.
Чим ближча хорда ця до центру, тим довшою стає вона.
Куля: Стривай ! А що , як через центр у хорди путь?
Коло : Діаметром вона стає тоді.
Куля: Діаметром… А скільки їх в тобі?
Коло: Ой нене! Безліч їх у мене. Дорівнює двом радіусам кожний.
Куля: А радіус?
Коло: Відрізок це, що сполуча мій центр із точками моїми –
Вже вам відомими малими.
Коли його ви збільшите в два рази , в два рази довшим стану й я.
Така властивість вже моя.
В мене властивостей багато. Одну вам варто нагадати.
Відношення довжини кола до діаметра для всіх нас є завжди незмінним,
Приблизно трьом і одній сьомій рівним.
За двісті літ до нашої ще ери його обчислив мудрий Архімед.
Майбутнє далеко вперед йому свої відкрило двері.
Відношення це у всьому світі знають і «пі» числом його всі називають.
Додаток 2. ( інструкція для роботи учнів )
- Знайдіть довжину ободу комп’ютерного диска за допомогою мірної стрічки:
l = …..
- Знайдіть довжину діаметра комп’ютерного диска ( діаметр – найдовша хорда):
d = ….
-
Обчисліть відношення
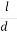 =
=
Додаток 3.
Позначення грецькою буквою П для відношення довжини кола до діаметра увів видатний математик Леонард Ейлер у 1737 році. П – перша буква грецького слова «периферія» , що означає «коло». До Ейлера в математичних науках це відношення не позначали ніяк або позначали щоразу по-іншому. Ще вавилоняни ( близько 2000р. до н.е.) встановили, що радіус шість разів уміщається в колі , як хорда; звідки було зроблено припущення, що довжина кола дорівнює шістьом радіусам або трьом діаметрам. Математики завжди намагалися якомога точніше знайти значення числа П. У 18 столітті було встановлено, що число П не можна подати у вигляді скінченного десяткового дробу. За допомогою сучасних комп’ютерів можна обчислити це число з величезною точністю, але, звичайно,практичного застосування таке значення не має. Найчастіше застосовують наближене значення числа до сотих: П= 3,14.
Додаток 4. Фізкультхвилинка.
Із – за парт ми миттю встали, гарно спинки підрівняли.
Вгору тягнемось усі, мов трава в дрібній росі.
Потім легко всі присіли , наче ноги заболіли.
Потім встали, руки в боки і зробити два підскоки.
Каблучками цок – цок і продовжим знов урок.


про публікацію авторської розробки
Додати розробку
