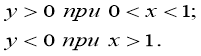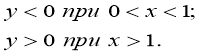Урок на тему "Логарифмічна функція"

Лисенко Олена Євгенівна

11 клас.

Алгебра і початки аналізу. Профільний рівень

Урок № 2

Тема: Логарифмічна функція

Мета: навчальна: формувати навички побудови логарифмічної функції,

          самостійної дослідницької діяльності учнів на уроці; підготовка до ЗНО

          з  математики;

           розвивальна: розвивати графічну культуру, вміння  аналізувати,

           порівнювати, інформаційно-комунікативні навички;

          виховна: формування таких якостей особистості, як відповідальність,

          уважність, організованість.

Тип уроку: комбінований урок

Обладнання: комп’ютер, мультимедійна дошка, програма Geogebra.

 

Найкращий спосіб вивчити що-небудь – це

відкрити самому.

Д. Пойа

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

 (Учитель робить заготовки для перевірки на слайдах).

 

 

 

 

 

 

 

 

 

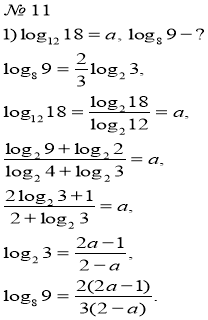
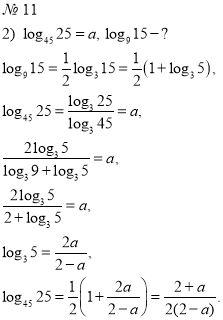
ІІІ. Актуалізація опорних знань

1. Вправа «Знайди пару». Для кожної функції знайдіть її графік http://LearningApps.org/display?v=pfack8czn16

 

 

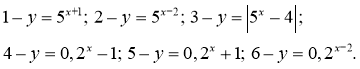
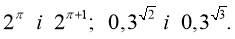2. Порівняйте:

На основі яких властивостей Ви зробили порівняння виразів?

(Властивості показникової функції)

IV. Проблемна ситуація

1. Створення проблемної ситуації

У 10 класі ми з Вами вивчили обернену функцію, її властивості. Назвіть функції, обернені до

Це відповідно такі функції

• А як знайти функцію, обернену до у = 2х+3?  
• Чи для кожної функції можна знайти обернену?
• Чи існує функція, обернена до показникової?

2. Розв’язання проблемної ситуації

• Знайдемо обернену функцію до у = 2х+3.

 

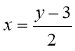
Виразимо  .

 

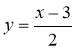
     Поміняємо змінні:  . Отримали обернену функцію до заданої.

 

• Якщо функція y = f(x) набуває кожного свого значення в єдиній точці її області визначення, то можна задати функцію y = g(x), яка називається оберненою до y = f(x). Властивості оберненої функції: якщо функція  f(x) зростає (спадає) на деякому проміжку, то вона має обернену функцію на цьому проміжку, яка зростає, якщо f(x) зростає, і спадає, якщо  f(x) спадає; графіки прямої та оберненої функцій симетричні відносно прямої у = х.
• Висновок: показникова функція має обернену функцію!

V. Оголошення теми уроку

   Отже, сьогодні на уроці ми з Вами будемо вивчати функцію, обернену до показникової – логарифмічну.

Означення:

Логарифмічною функцією називається функція виду 

 

VІ. Осмислення нового матеріалу

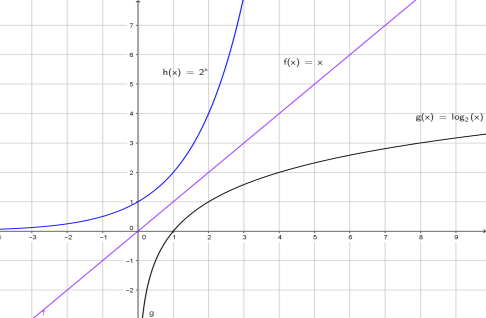
   Працюючи над проблемою, Ви вже знайшли шлях побудови графіка даної функції.

 

Покрокова побудова:

http://ggbm.at/VUWhYxyP.

 

 

 

 

 

1. 
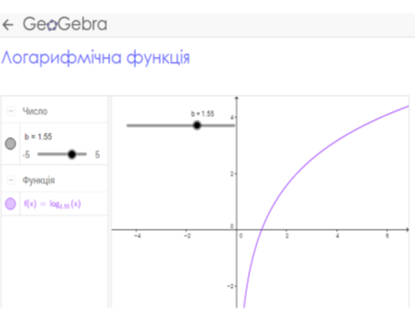
   Розглянемо властивості логарифмічної  функції:

 

http://ggbm.at/mGsx6V4W.

Заповнимо таблицю:

Властивості
Область визначення
Область значень
Проміжки зростання і спадання	Функція спадає на всій області визначення	Функція зростає на всій області визначення
Проміжки знакосталості

Знайдіть точки перетину графіка функції з осями координат. ( З віссю ОУ немає точок перетину, з ОХ – точка (1; 0).

Чи буде логарифмічна функція парною чи непарною? Обгрунтуйте!

(Функція не буде ні парною, ні непарною – це можна визначити по області визначення, а також по графіку, оскільки симетрії відносно початку відліку системи координат або відносно осі ОУ не існує).

2. Побудова графіків логарифмічних функцій за допомогою геометричних перетворень.

http://ggbm.at/nvWNayZv

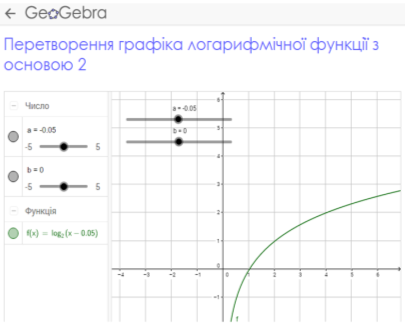
VІІ. Розв’язування вправ

1. §16, № 4

Порівняйте числа:

 

 

Основа функції                     більша від 1, отже функція зростає на всій області визначення

 

Основа функції                      0 < 0,1 < 1, отже функція спадає на всій області визначення                                   .

7)

                            , отже                   .

2. §16, № 1

Знайдіть область визначення функції:

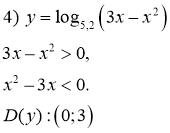2)

    

 

 

 

 

 

 

 

 

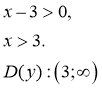
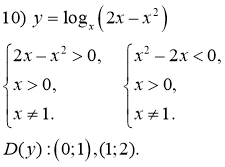
VIІІ. Підсумок уроку

  Оцінювання діяльності учнів на уроці.

Рефлексія діяльності:

На дошці заготовка – «рефлексивна мішень» (слайд 10). В  учнів на партах стікери одного кольору. Діти підходять до мішені і розміщують стікери у секторах: «Активно брав участь», «Було цікаво», «Було зрозуміло», «Дізнався нове». Чим ближче стікер до центру мішені, тим їхня самооцінка діяльності на уроці вища. Проводимо короткий аналіз «рефлексивної мішені».

IX. Домашнє завдання

1. Вивчити § 16.
2. Виконати завдання § 16,  № 3 (4, 7, 9),  № 6.

Нелін Є. П. Алгебра. 11 клас: підручник для загальноосвітніх навчальних закладів: академ. рівень, проф. рівень / Є. П. Нелін, О. Є. Долгова. – Харків: Гімназія, 2011. – 448 с.