Урок на тему: "Об'єм піраміди. Розв’язування задач"
Тема. Об'єм піраміди. Розв’язування задач.
Мета уроку: узагальнити та систематизувати вміння практично використовувати набуті теоретичні знання при розв’язуванні задач, формувати навички контролю та самоконтролю своїх навчальних досягнень; розвивати просторові уявлення, логічне мислення; виховувати почуття взаємодопомоги, взаємопідтримки, наполегливість.
Обладнання: картки, таблиця, презентація, мультимедійний проектор.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
І. Організаційний етап.
ІІ. Перевірка домашнього завдання.
№1(усно), №2
III. Формування теми, мети і завдань уроку. Мотивація навчальної діяльності.
Єгипет – країна пірамід. Самі знамениті три великі піраміди біля Гізи: Хеопса (Хуфу), Хефрена(Хафра) і Мекеріна (Менкаура) . Найбільша з них піраміда Хеопса. Це саме найдавніша з семи чудес світу до того ж ідеально збереглася до наших часів, споруджена в 28 столітті до нашої ери. Спочатку вона піднімалася на147 метрів, але через наступ пісків її висота зменшилася до 137 метрів. Кожна сторона квадратної основи піраміди складає 233 метра. Давайте визначимо у скільки разів зменшився об’єм піраміди?
IV. Актуалізація знань, умінь та навичок
Мікрофон
1.Чому дорівнює об 'єм піраміди ?
2. Чому дорівнює об 'єм правильної чотирикутної піраміди?
3.Як зміниться об 'єм правильної чотирикутної піраміди, якщо сторону основи ззалишити незмінною, а висоту зменшити на 100 м?
4. Переріз, проведений паралельно основі піраміди ділить її на два тіла
( піраміду і зрізану піраміду). Як відносяться об 'єми піраміди й зрізаної піраміди?
Як приємно дізнатися, що ти чогось навчився.
Мольєр
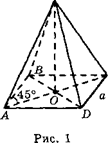Розв’язування задач за готовими малюнками
1.Обчисліть об’єм правильної піраміди
Недостатньо лише отримати знання;
треба знайти їм застосування.
Недостатньо тільки бажати;
треба творити.
Йоган Гете
Робота в парах.
Тест.
Позначте на вашу думку правильну відповідь.
- Площа основи трикутної піраміди 3 см2, а висота – 3 см. Укажіть її об’єм
|
А |
Б |
В |
Г |
|
1см3 |
3 см3 |
9 см3 |
|
- Якщо сторони основи правильної n - кутної трикутної піраміди зменшити в 3 рази при незмінній висоті, то її об’єм зменшиться:
|
А |
Б |
В |
Г |
|
В 3 рази |
В 3n разів |
В 9 разів |
В |
3. Знайдіть об’єм піраміди, основою якої є прямокутний трикутник з катетами 2 см і 3см, висотою 4см. ( слайд )
|
А |
Б |
В |
Г |
|
4см3 |
10 см3 |
12 см3 |
40 см3 |
4. Знайдіть об’єм піраміди з висотою 10 см, основою якої є ромб із діагоналями 5см, 9см ( слайд )
|
А |
Б |
В |
Г |
|
60 см3 |
75 см3 |
120 см3 |
150 см3 |
5. Знайдіть об’єм правильної шестикутної піраміди з висотою 
3 см, а бічне ребро становить 2 см. ( слайд )
|
А |
Б |
В |
Г |
|
1,5 см3 |
3 см3 |
3,6 см3 |
7,2 см3 |
Самоперевірка робіт.
V. Застосування знань, умінь та навичок.
Теорія без практики мертва і безплідна, практика без теорії неможлива.
Р. Декарт.
Розв’язування задач.
№1
В основі піраміди лежить рівнобедрений трикутник з основою 12 см і кутом 60º при вершині. Усі бічні ребра піраміди утворюють з площиною основи кут 30º. Знайдіть об’єм піраміди.
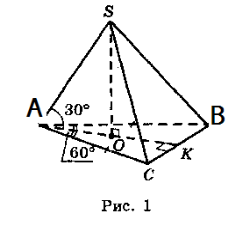
Дано трикутну піраміду SАВС , основа якої рівнобедрений трикутник АВС, ВС=12см, <ВАС= 60º.
Так як всі ребра піраміди утворюють з площиною основи кути по 30º, тоді точка О є центром описаного кола навколо трикутника АВС, АО= R, радіус описаного кола.
Проведемо АК 
ВС, АК – медіана, висота, бісектриса трикутника АВС.
О належить АК.
SО ( АВС), тоді АО проекція АS на площину основи і <SАО= 30º
Знайдемо об’єм піраміди.
Відповідь: 48 3см3.
№2
Основою піраміди є прямокутний трикутник із катетом b і протилежним йому гострим кутом β. Дві бічні грані, які містять катети цього трикутника, перпендикулярні до площини основи, а третя нахилена до неї під кутом α.
Знайдіть об’єм піраміди.
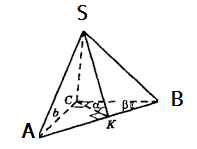
Нехай основою піраміди SАВС є прямокутний трикутник АВС із катетом b і протилежним йому гострим кутом β.
Так як бічні грані, які містять катети цього трикутника SСА і SСВ, перпендикулярні до площини основи піраміди, то їх спільне ребро SС є висотою піраміди. Проведемо СК АВ , тоді SК АВ за теоремою про три перпендикуляри, звідси < SКС= α - кут нахилу грані SАВ до площини основи піраміди. Знайдемо об’єм піраміди.
Відповідь: 1/6 b3 ctg β cos β tg α.
Робота в групах.
Збиратися разом - це початок,
Триматися разом – це процес,
Працювати разом – це успіх
Генрі Форд
1 група С
№1
Знайдіть об’єм правильної трикутної піраміди, бічне ребро якої дорівнює
7 см, а сторона основи 23см.
2 група Д
№ 2
Основа піраміди – трикутник зі сторонами 13см, 14см, 15см. Двогранні кути при кожному ребрі основи дорівнюють по 45º . Знайдіть об’єм піраміди.
3 група В
№ 3
Основа піраміди – рівнобедрений трикутник із бічною стороною b і кутом при основі β . Усі двогранні кути при ребрах основи α. Знайдіть об’єм піраміди.
VI. Підсумок уроку
Учитель коментує роботу кожної групи. Оцінює роботу учнів на уроці.
VII. Домашнє завдання
«Все боїться часу, а час боїться пірамід» – твердження давнє, але більш ніж вірне.
Піраміда Джосера – одна з найбільших в Єгипті, крім великих пірамід Гізи, знаходиться в селі Саккара і є однією з найбільш древніх великих споруд у світі. Побудував її Імхотеп, як гробницю для фараона Джосера, в 2650 до нашої ери. Її також називають Ступінчастою пірамідою через особливу форму. Це чудо складається з 6 ступенів.
Знайти розміри піраміди Джосера , обчислити її об'єм.
про публікацію авторської розробки
Додати розробку