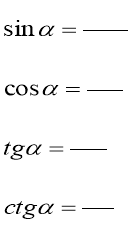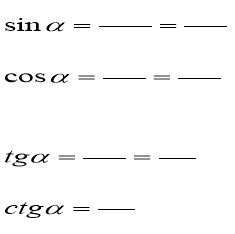Урок на тему "Означення синуса, косинуса, тангенса кутів від 0 градусів до 180"
Урок розроблений відповідно до сучасних вимог - залучення дітей до самостійного активного оволодіння новим матеріалом. Створюється проблемна ситуація, над якою і працюють діти. Створена доповняльна реальність в додатку Blippar зацікавлює дітей, мотивує їх, "оживляє" сторінки підручника.
Лисенко Олена Євгенівна
Урок № 1
Тема: Синус, косинус, тангенс кута від 00 до 1800
Мета: навчальна: сформувати означення синуса, косинуса, тангенса кута від 00 до 1800, удосконалювати навички самостійної дослідницької діяльності учнів на уроці;
розвивальна: розвивати вміння аналізувати, порівнювати, критично мислити, обґрунтовувати свій вибір, інформаційно-комунікативні навички;
виховна: формування таких якостей особистості, як відповідальність, уважність, організованість, вміння працювати в групі
Тип уроку: урок вивчення нового матеріалу
Обладнання: проектор, комп’ютер, смартфони, програма Blippar, встановлена на смартфонах у дітей, ресурс Learningapps, роздаткові картки: «Помічник», зображення-маркер для створення доповненої реальності
Хід уроку
Самостійні думки виникають
тільки із самостійно отриманих знань
К. Ушинський
І. Організаційний момент
Сьогодні ми з вами розпочинаємо вивчення нової теми. Як на вашу думку, чому епіграфом уроку я вибрала саме ці слова. (Вислухати думки дітей)
Так, ви праві, сьогодні ви самі будете відкривати для себе нову, цікаву сторінку геометрії!
ІІ. Підготовка до вивчення нового матеріалу
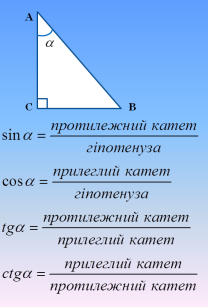
Працюємо в парах по картці «Помічник». Повторюємо вивчене – вже відомі означення для дітей, і заповнюємо в картці перше завдання.
Картка «Помічник»
|
|
А тепер самі:
Для даного ∆ АВС знайдіть:
|
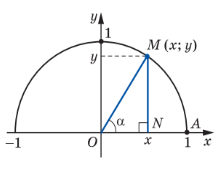
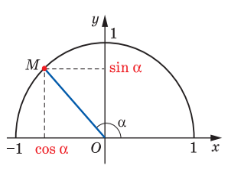
Перед Вами півколо одиничного радіусу, по якому рухається точка М (х; у).
|
Знайдіть для ∆ МОN:
|
|
Запишіть ваші міркування:
|
ІІІ. Постановки проблеми:
- З яким трикутником ви працювали?
- Які особливості прямокутного трикутника?
- Які ще види трикутників ви знаєте?
- Як ми знаємо, кут може бути більший 900, як же тоді працюватимуть відомі нам означення синуса, косинуса, тангенса кута?
- Чи залишаться вони без зміни?
Саме на ці питання ми і будемо шукати відповіді на уроці!
IV. Вивчення нового матеріалу
- Повернемося до картки «Помічник». У парах попрацюйте над другим
завданням. Обговоріть, чому виникла потреба звернутися до півкола одиничного радіуса? Чи завжди для точки, що рухається по одиничному колу, можна визначити синус, косинус, тангенс кута? Зробіть відповідні записи у 2 і 3 завданні!
Проводимо обговорення і отримуємо шукані означення синуса, косинуса, тангенса кута від 00 до 1800.
Косинусом і синусом кута (00 ≤ ≤ 1800) називають відповідно абсцису і ординату точки М одиничного півкола, яка відповідає куту .
 Тангенсом (котангенсом) кута (00 1800) називають відповідно відношення ординати до абсциси (абсциси до ординати) точки М одиничного півкола, яка відповідає куту . Для якого з цих кутів тангенс не існуватиме? (900)
Тангенсом (котангенсом) кута (00 1800) називають відповідно відношення ординати до абсциси (абсциси до ординати) точки М одиничного півкола, яка відповідає куту . Для якого з цих кутів тангенс не існуватиме? (900)
У чому полягає відмінність для синуса (косинуса) гострого і тупого кутів?
Косинус тупого кута від’ємне число, бо абсциса точки в ІІ чверті від’ємна.
- «Живий» підручник.
Переходимо до роботи з підручником – сторінка 7. Опрацьовуємо і використовуємо роздруковану сторінку як маркер для створення доповненої реальності.


Рис. 1 Рис. 2
Діти відкривають на смартфонах додаток Blippar, сканують зображення (рис. 1) і потрапляють до «живого» зображення (рис. 2). Код для створеної вправи – 922279. Під об’єктом «піраміда» захована цікава інформація про розвиток понять «синус і косинус» кута (http://factosvit.com.ua/chomu-synus-tak-nazvaly/), під об’єктом «конус» -
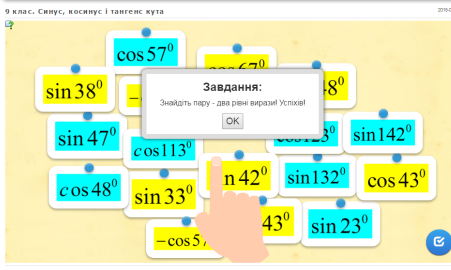
інтерактивна вправа (https://learningapps.org/watch?v=pkca32v9n18), яку учні виконують на закріплення вивченого матеріалу.
V. Розв’язування вправ
№ 1.2, 1.4, 1.8, 1.14, 1.17.
VІ. Підсумок
Продовжіть речення:
- Я сьогодні дізнався…
- Я для себе відкрив …
- Я навчився …
- Я хочу дізнатися …
- Мені було найважче …
- Мені було найцікавіше …
- Я хочу ще раз закріпити …
- Я впевнився …
- Я зрозумів, що все в моїх руках, …
VІІ. Домашнє завдання:
§ 1, п.1, стор. 5-7 – вивчити, розв’язати - № 1.5, 1.9, 1.18.
Мерзляк А. Г. Геометрія: підручник для 9 класів загальноосвітніх навчальних закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Харків: Гімназія, 2017. – 240 с. : іл.
-
супер

про публікацію авторської розробки
Додати розробку