Урок на тему "Показникова функція"
Тема уроку: Показникова функція, її графік і властивості.
Мета уроку:
Навчальна:
- шляхом комп’ютерного експерименту привести учнів до розуміння і засвоєння властивостей показникової функції та властивості її графіка ;
- формувати уміння застосовувати електроні таблиці Microsoft Excel як засіб дослідження математичних функцій.
Розвивальна:
- розвивати вміння знаходити інформацію за допомогою ІКТ;
- формувати операції мислення – аналіз, доведення, узагальнення, класифікація.
Виховна:
- виховувати бережливе ставлення до шкільного майна;
- сприяти підтримці на високому рівні загальної працездатності до навчання;
- виховувати волю і наполегливість в учнів для досягнення кінцевих результатів.
Тип уроку: засвоєння нових знань.
Обладнання: комп’ютерний клас (10 комп’ютерів), мультимедійний проектор, роздатковий матеріал.
Епіграф уроку:
Не достатньо мати добрий розум,
головне – це раціонально застосовувати його.
Р. Декарт
Хід уроку
- Організація класу
- Мотивація пізнавальної діяльності
Багато процесів у природі і техніці математично виражаються за допомогою показникової функції. А саме:
1) задача про радіоактивний розпад;
2)задача про зміну атмосферного тиску;
3) задача про вакуумування;
4) задача про розмноження бактерій;
5) задача про приріст деревини.
Але, щоб вміти розв’язувати дані задачі треба знати властивості показникової функції.
- Повідомлення теми уроку
- Сприймання і усвідомлення нового матеріалу
Функція виду ![]() , називається показникової (з основою а).
, називається показникової (з основою а).
Почнемо вивчення показникових функцій з функцій :
1 пара: ![]() ;
;
2 пара![]() ;
;
3 пара: ![]() ;
;
4 пара: ![]() ;
;
5 пара: ![]() ;
;
6 пара: ![]() ;
;
7 пара: ![]() ;
;
8 пара: ![]() .
.
Побудувати графіки даних функцій в програмі Microsoft Excel та описати їх властивості за такою схемою:
Схема
- область визначення функції;
- область значень функції;
- монотонність функції;
- точки перетину графіка функції з осями координат.
Пари 1 – 4 об’єднуються в групу «А» і обговорюють властивості функції виду ![]() , готують виступ і відповіді на поставлені питання.
, готують виступ і відповіді на поставлені питання.
Усне виконання вправ
- Чи є серед значень функції у=2х:
а) найбільше; б) найменше?
Відповідь: ні.
- Порівняйте значення виразів:
а) ![]()
Відповідь: а) ![]()
-
Розташуйте числа
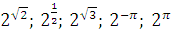 у порядку зростання.
у порядку зростання.
Відповідь: ![]()
![]()
- Порівняйте х і у, якщо відомо, що вірна нерівність:
а) 2х > 2у; б) 2х < 2у.
Відповідь: а) х>у; б) х<у.
- На рисунку 86 із підручника зображено графіки функцій у=2х і у=3х. Чим відрізняються ці функції? Їхні графіки?
Відповідь: ці функції мають однакові властивості, функція у=3х зростає більш швидше (графік цієї функції піднімається вгору більш круто)
Пари 5 – 8 об’єднуються в групу «Б» і обговорюють властивості функції виду ![]() , готують виступ і відповіді на поставлені питання.
, готують виступ і відповіді на поставлені питання.
Усне виконання вправ
-
Чи є серед усіх значень функції у=
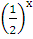 :
:
а) найбільше; б) найменше?
Відповідь: ні.
- Порівняйте значення виразів:
а) ![]()
![]() д)
д) ![]() .
.
Відповідь: а) ![]()
![]() д)
д) ![]() .
.
-
Розташуйте числа
 ,
, 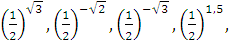 у порядку зростання.
у порядку зростання.
Відповідь: ![]()
- Порівняйте х і у, якщо відомо, що вірна нерівність:
а) ![]()
Відповідь: а) х < у; б) х > у.
-
Порівняйте як розташовані графіки функцій у=2х і у=
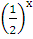
Відповідь: графіки розташовані симетрично відносно осі OY.
- Чим відрізняються властивості і графіки функцій
у =![]() і у =
і у = ![]() ?
?
Відповідь: вони мають однакові властивості, функція у = ![]() спадає більш швидше.
спадає більш швидше.
- Систематизація і осмислення вивченого матеріалу
Після обміну інформацією між групами, учні роблять загальні висновки:
- властивості показникової функції ;
- властивості графіка показникової функції.
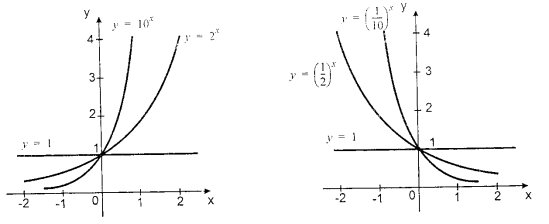
Властивості показникової функції
|
Властивості |
Функція у = ах |
|
|
0<a<1 |
|
|
1).Область визначення D(y). |
x |
x |
|
2).Множина значень E(y). |
y>0; E(y) = (0;+ |
y>0; E(y) = (0;+ |
|
Показникова функція набуває лише додатних значень ax >0 завжди ! Графік не перетинає осі Ox. |
||
|
3).Значення у для х=0. |
х=0; у=1. |
х=0; у=1. |
|
Графік перетинає вісь Oy в точці (0;1). |
||
|
4).Значення у для x <0.
|
x>0; y>1. ax >1, при x <0. |
x>0; 0<y<1. 0< ax<1, при x>0. |
|
5).Значення у для x >0. |
x<0; 0<y<1. 0< ax<1, при x<0. |
x<0; y>1. ax>1, при x<0. |
|
6).Монотонність. |
Зростає на всій числовій прямій (більшому показнику відповідає більший степінь). |
Спадає на всій числовій прямій (більшому показнику відповідає менший степінь). |
|
Наслідок. Якщо два степені одного і того самого додатного числа, відмінного від 1, рівні, то рівні і їх показники. Якщо ab =ac,то b=c. |
||
Властивості графіка показникової функції.
Графік показникової функції називається експонентною.
|
Властивості графіка показникової функції.
|
|
|
1).Графік розміщений у верхній півплощині, тобто там, де ординати додатні. |
1).Графік розміщений у верхній півплощині, тобто там, де ординати додатні. |
|
2).Будь-яка пряма, паралельна осі Oy, перетинає графік і до того ж тільки в одній точці. |
2).Будь-яка пряма, паралельна осі Oy, перетинає графік і до того ж тільки в одній точці. |
|
3).Крива проходить через точку (0;1), тобто коли х =0, функція чисельно дорівнює 1. |
3).Крива проходить через точку (0;1), тобто коли х =0, функція чисельно дорівнює 1. |
|
4).З двох точок графіка вище розміщена та, яка лежить правіше, тобто в міру просування зліва направо він піднімається вгору. |
4).З двох точок графіка вище розміщена та, яка лежить лівіше, тобто в міру просування справа наліво він піднімається вгору. |
|
5).На графіку є точки, які лежать вище будь-якої прямої, паралельної осі Ox. На графіку є точки, що лежать нижче будь-якої прямої, проведеної у верхній півплощині паралельно осі х. Лівою своєю частиною графік, якщо рухатися за ним справа наліво, все ближче підходить до осі х, але не дотикається до неї. |
5).На графіку є точки, які лежать вище будь-якої прямої, паралельної осі Ox. На графіку є точки, що лежать нижче будь-якої прямої, проведеної у верхній півплощині паралельно осі х. Правою своєю частиною графік, якщо рухатися за ним зліва направо, все ближче підходить до осі х, але не дотикається до неї. |
|
6).Будь-яка пряма, що паралельна осі х і лежить у верхній півплощині, перетинає графік, і причому в одній точці. |
6).Будь-яка пряма, що паралельна осі х і лежить у верхній півплощині, перетинає графік, і причому в одній точці. |
Приклади застосування властивостей показникової функції.
-
Що можна сказати про числа m і n, якщо
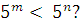
-
Що можна сказати про числа p і q, якщо
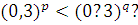
-
Що можна сказати про додатну основу a, якщо

- Який висновок можна зробити відносно додатної основи a,
якщо ![]()
- Який висновок можна зробити про додатну основу a,
![]()
-
Що можна сказати про число m, якщо
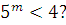
- На основі властивостей показникової функції замінити знак V в кожному з наступних випадків знаком >,<,=.
а) ![]()
г) ![]() V
V ![]()
- Вказати, які з показникових функцій
![]()
-
Які з функцій
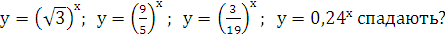
-
Дано кілька зростаючих функцій:
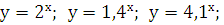
![]() зростання для x>0
зростання для x>0
Підсумок уроку.
Рефлексія.
- Що нового дізналися?
- Чи продуктивною була ваша праця на уроці?
Домашнє завдання.
- підготувати презентацію на тему «Показникова функція, її графік і властивості» (Додаток)


про публікацію авторської розробки
Додати розробку
