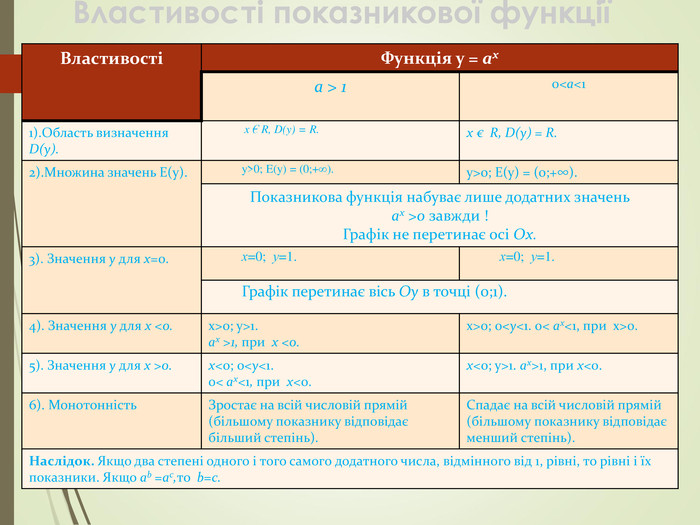
презентація на тему "Показникова функція"

Показникова функція, її графік і властивості.

Мета уроку: Навчальна: шляхом комп’ютерного експерименту привести учнів до розуміння і засвоєння властивостей показникової функції та властивості її графіка ; формувати уміння застосовувати електроні таблиці Microsoft Excel як засіб дослідження математичних функцій.

Розвивальна: розвивати вміння знаходити інформацію за допомогою ІКТ; формувати операції мислення – аналіз, доведення, узагальнення, класифікація. Виховна: виховувати бережливе ставлення до шкільного майна; сприяти підтримці на високому рівні загальної працездатності до навчання; виховувати волю і наполегливість в учнів для досягнення кінцевих результатів.

Епіграф уроку: Не достатньо мати добрий розум, головне – це раціонально застосовувати його. Р. Декарт

Схема область визначення функції; область значень функції; монотонність функції; точки перетину графіка функції з осями координат.

Властивості показникової функції Властивості Функція у = ах a > 1 00; E(y) = (0;+∞). y>0; E(y) = (0;+∞). Показникова функція набуває лише додатних значень ax >0 завжди ! Графік не перетинає осі Ox. 3). Значення у для х=0. х=0; у=1. х=0; у=1. Графік перетинає вісь Oy в точці (0;1). 4). Значення у для x <0. x>0; y>1. ax >1, при x <0. x>0; 00. 5). Значення у для x >0. x<0; 01. ax>1, при x<0. 6). Монотонність Зростає на всій числовій прямій (більшому показнику відповідає більший степінь). Спадає на всій числовій прямій (більшому показнику відповідає менший степінь). Наслідок. Якщо два степені одного і того самого додатного числа, відмінного від 1, рівні, то рівні і їх показники. Якщо ab =ac,то b=c.

Властивості графіка показникової функції Властивості графіка показникової функції. a > 1 0

Приклади застосування властивостей показникової функції. Що можна сказати про числа m і n, якщо Що можна сказати про числа p і q, якщо Що можна сказати про додатну основу a, якщо Який висновок можна зробити відносно додатної основи a, якщо Який висновок можна зробити про додатну основу a, Що можна сказати про число m, якщо

На основі властивостей показникової функції замінити знак V в кожному з наступних випадків знаком >,<,. = а) г) V Вказати, які з показникових функцій Які з функцій Дано кілька зростаючих функцій: зростання для x>0

Чи є серед значень функції у=2х: а) найбільше; б) найменше? Порівняйте значення виразів: а) Розташуйте числа у порядку зростання Порівняйте х і у, якщо відомо, що вірна нерівність: а) 2х > 2у; б) 2х < 2у. На рисунку 86 із підручника зображено графіки функцій у=2х і у=3х. Чим відрізняються ці функції? Їхні графіки?

Чи є серед усіх значень функції у= : а) найбільше; б) найменше? Порівняйте значення виразів: а) д) Розташуйте числа у порядку зростання. Порівняйте х і у, якщо відомо, що вірна нерівність: а) Порівняйте як розташовані графіки функцій у=2х і у= , користуючись рис. 88 із підручника. Чим відрізняються властивості і графіки функцій у = і у =

Підсумок уроку Рефлексія. Що нового дізналися? Чи продуктивною була ваша праця на уроці? Домашнє завдання. підготувати презентацію на тему «Показникова функція, її графік і властивості.»