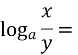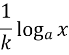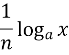Логарифмічні рівняння. Корекція знань та умінь учнів.
Добровеличківський ліцей « Інтелект»
Добровеличківської районної ради
Тема уроку: Логарифмічні рівняння. Корекція знань та умінь учнів.
Мета: навчальна: учень обгрунтовує розв’язки найпростіших логарифмічних рівнянь та розв’язує нескладні логарифмічні рівняння;
розвивальна: розвивати математичне мовлення; логічне мислення, пам'ять, увагу;
виховна: виховувати працелюбність, прививати бажання мати якісні глибокі знання, виховувати зібраність, організованість, відповідальність, культуру міжособистісного спілкування, вміння працювати в команді; готовність свідомо приймати та виконувати рішення.
Обладнання: підручник, роздатковий матеріал, зміст самостійної роботи, презентація.
Тип уроку: узагальнення та систематизація.
Хід уроку
І. Організаційний етап
Налаштування на роботу.
Деякі учні, а то і дорослі, вважають, що математика - це суха і нецікава наука. Доведемо протилежне. Покажемо взаємозв'язок математики з іншими предметами; покажемо, що математика – не тільки строга система законів, правил та задач, але і унікальний засіб пізнання краси. Сьогодні ми з вами поринемо в світ чудовий та прекрасний – в світ математичних рівнянь.
Розпочнемо наш урок словами Джорджа Пойя:
«Уміння розв’язувати математичні задачі— практичне мистецтво, подібне плаванню, або катанню на лижах, або грі на фортепіано: навчитися цьому можна, лише постійно тренуючись...»
ІІ. Інтерактивна вправа «Вимірювання температури»
Перед вами на парті лежать « термометри» , зробіть зліва позначку, що відповідає рівню ваших знань з теми « Логарифми, їх властивості. Логарифмічні рівняння»
 Що я знаю про логарифми та логарифмічні рівняння
Що я знаю про логарифми та логарифмічні рівняння
![]()

![]()
![]()
ІІІ. Інтерактивна вправа «Знайди пару».
Робота в малих групах
При розв’язуванні логарифмічних рівнянь нам не обійтись без властивостей логарифмів та деяких логарифмічних тотожностей. Учням, які отримають конверт, потрібно об’єднатися в пари та за 5хв. виконати таке завдання:
Завдання. Скласти формули, які відображують властивості логарифмів та логарифмічні тотожності.
|
1 |
|
0 |
т |
|
2 |
|
1 |
0 |
|
3 |
|
|
л |
|
4 |
|
|
е |
|
5 |
|
|
р |
|
6 |
|
|
а |
|
7 |
|
|
н |
|
8 |
|
|
т |
|
9 |
|
|
н |
|
10 |
|
|
і |
|
11 |
|
|
с |
|
12 |
|
|
т |
|
13 |
|
|
ь |
Толерантність — це терпимість до чужих думок, вірувань, поведінки. Це повага або визнання рівності інших, відмова від домінування чи насильства.
16 листопада – міжнародний день толерантності.
Його запровадили у 1996 році за рішенням Генеральної Асамблеї ООН. Саме цього дня ЮНЕСКО ухвалило «Декларацію принципів терпимості».
Статтею 6 була урочисто проголошена дата щорічного святкування події.
У Декларації йдеться про рівність усіх людей, незалежно від їхнього віросповідання, етнічної належності чи кольору шкіри.
Як заявлено в Декларації принципів толерантності (від лат. tolerantia — терпіння), «терпимість – це те, що робить можливим досягнення миру та веде від культури війни до культури миру».
Терпимість, означає повагу, прийняття та правильне розуміння багатого різноманіття культур нашого світу, наших форм самовираження і способів вияву людської індивідуальності. Їй сприяють знання, відкритість, спілкування та свобода думки, совісті та переконань.
Терпимість – це гармонія у різноманітті. Це не тільки моральний обов’язок, але й політична та правова потреба. Прояв толерантності який співзвучний принципу поваги до прав людини, не означає терпиме ставлення до соціальної несправедливості, злочинів та правопорушень, відмову від своїх поглядів або поступки перед чужими переконаннями.
Толерантність (терпимість) означає, що кожен вільний дотримуватися своїх переконань і визнавати таке ж право за іншими.
Мир не можливий без терпимості, а розвиток та демократія неможливі без миру. Сьогодні варто замислитися над цим і зробити себе і світ хоч на краплину добріше та толерантніше.
Саме цьому мистецтву – жити з людьми і серед людей присвячений День толерантності, який відзначають у всьому світі.
ІV. Мотивація навчальної діяльності
Ми закінчуємо з вами вивчати розділи алгебри «Показникові та логарифмічні функцїї», які мають величезне значення для природничих дисциплін. Вміння розв'язувати показникові та логарифмічні рівняння використовують в біології, хімії, географії, економіці, фізиці - інтенсивність звуку (децибели), астрономії - шкала яскравості зірок, сейсмологія - шкала Ріхтера, теорія музики - нотна шкала, по відношенню до частот нотних звуків.
Альберт Енштейн казав: «Мені доводиться ділити свій час між політикою та рівняннями. Проте рівняння, як на мене, набагато важливіше, тому що політика існує тільки для даного моменту, а рівняння будуть існувати вічно».
Учням пропонується переглянути презентацію «Логарифми навколо нас». Підбір матеріалу до презентації, створення і проведення презентації виконують учні. (випереджальне завдання).
 І .Історія
І .Історія
Логарифм – з грецької означає “логос”- відношення і “аритмос”- число.
Протягом XVI ст. значно зросла кількість наближених обчислень, що було зумовлено розв'язуванням прикладних задач (особливо в астрономії). Інтерес до астрономії призводить до вивчення математики.
Логарифм, яким ми знаємо його сьогодні, вперше був запропонований Джоном Непером - англійським математиком (1550-1617), який в ході своїх досліджень, вивів новий, більш простий шлях складних числових розрахунків. Він показує, що якщо ввести експоненту, операції множення і ділення великих чисел перетворюються в просте додавання експонент.
 Відкриття Непера було представлено публіці в 1614 р. в його книзі “Mirifici logarithmorum canonis descriptio” ( «Опис дивовижної таблиці логарифмів»). У даній роботі він лише коротко описує кроки, які призвели до цього відкриття, основні зусилля зосереджуються на демонстрації перших таблиць логарифмів. Понад три з половиною сторіччя з тих пір, як у 1614 році були опубліковані Непером перші логарифмічні таблиці, вони вірою і правдою служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький вчений Лаплас , продовжуючи життя обчислювачам.
Відкриття Непера було представлено публіці в 1614 р. в його книзі “Mirifici logarithmorum canonis descriptio” ( «Опис дивовижної таблиці логарифмів»). У даній роботі він лише коротко описує кроки, які призвели до цього відкриття, основні зусилля зосереджуються на демонстрації перших таблиць логарифмів. Понад три з половиною сторіччя з тих пір, як у 1614 році були опубліковані Непером перші логарифмічні таблиці, вони вірою і правдою служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький вчений Лаплас , продовжуючи життя обчислювачам.
Десяткові логарифми ввів англійський математик Генрі Брігс, у 1617 році видав перші таблиці десяткових логарифмів.
Сучасне означення логарифма числа сформулював відомий математик, фізик, астроном Леонард Ейлер. Він увів позначення log і букву![]() як основу натурального логарифму
як основу натурального логарифму ![]()
Ейлер грунтовно досліджував показникові та логарифмічні функції, називаючи їх «показниковими та логарифмічними кількостями»
 Перший варіант логарифмічної лінійки розробив англійський математик-аматор Вільям Отред у 1622 році. Логарифмічну лінійку неодноразово вдосконалювали і до 70-х років ХХ ст вона була незамінним інструментом інженера.
Перший варіант логарифмічної лінійки розробив англійський математик-аматор Вільям Отред у 1622 році. Логарифмічну лінійку неодноразово вдосконалювали і до 70-х років ХХ ст вона була незамінним інструментом інженера.
І хоч тепер її витіснили калькулятори і комп’ютери, проте можна сміливо сказати, що без логарифмічної лінійки не було і перших комп’ютерів.
Логарифмічні рівняння в біології, хімії, фізиці.
Борис Володимирович Гнеденко писав : «В наше сучасне життя втручається математика з її особливим стилем мислення, яке стає зараз обов’язковим і для інженера, і для біолога»
При розв'язуванні задач з біології використовують формули, що містять логарифми:
- Задача. Чисельність популяції складає 5 000, останнім часом, вона щорічно зменшувалася на 8%. Коли чисельність популяції досягне 2 000 вона почне вимирати. Скільки років залишилось існувати популяції?
Логарифми в хімії
Розчини в природі можуть мати різну реакцію середовища: кислу, лужну, нейтральну, що характеризується різною концентрацією йонів Гідрогену С( Н+). Для зручності було введено термін «водневий показник» (рН). Водневий показник — величина, що показує міру активності іонів водню (Н+) в розчині, тобто ступінь кислотності або лужності цього розчину.
Водневий показник - це від'ємний десятковий логарифм концентрації йонів Гідрогену
рН = - lg С( Н+)
Вперше це поняття було введено в науку шведським хіміком Еріком Зеренсеном в 1909 році.
Говорячи науковою мовою, рН - це показник кислотності, який залежить від рівня концентрації вільних водневих іонів. Даний показник коливається від 1 до 14, а 6,5-7,5 - його нейтральне значення, яке відповідає звичайній воді.
Показник рН в біологічних розчинах
|
Рідина |
рН |
Рідина |
рН |
|
Шлунковий сік |
1,4 |
Сеча |
6,0 |
|
Сік лимона |
2,1 |
Слина,молоко |
7,4-8 |
|
Сік яблук "Антонівка" |
2,5 |
Слюзи |
7,0 |
|
Томатний сік |
4,1 |
Кров |
7,4 |
З таблиці видно, що різні розчини в людському організмі мають різний рН, його відхилення від норми спричиняє захворювання і навіть загибель організму. Людям з підвищеною кислотністю шлункового соку рекомендується пити мінеральну воду з вищим рН, а зі зниженою кислотністю - "кислішу" воду(з нижчим рН).
У наш час практично жодна реклама косметичної продукції не обходиться без інформації про рН.
Всі косметичні препарати з рН менше 7 - кислі (рідке мило, бальзами, ополіскувачі, лікувальна косметика, креми з фруктовими кислотами і т. д.). Якщо рН більше 7 - препарати лужні (тверде туалетне мило, фарби для волосся, тверді дезодоранти і т. д.)
Вибираючи косметичні препарати, слід виходити насамперед з показника рН шкіри, який коливається від 3 до 7.
Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення рН. Більшість рідких косметичних засобів має рН 5,5.
При розв'язуванні задач з біології використовують формули, що містять логарифми:
Задача 2. Обчислити pH розчину соляної кислоти, якщо С = 0,003 моль/г
Задача 3. На скільки градусів потрібно підвищити температуру для прискорення хімічної реакції в 5 900 разів, якщо швидкість реакції зростає за геометричною прогресією зі знаменником, що дорівнює 3 при підвищені температури на кожні 100.
Фізика та астрономія завжди вимагають математичних розрахунків, тому знання математики у фізиці та астрономії завжди необхідні.
Наприклад в астрономії. Збільшення діаметра об'єктива телескопа дозволяє бачити кількість зірок, які не можна розрізнити простим оком. При цьому гранична «зіркова величина» ![]() зірок, які можна побачити через телескоп, обчислюється за формулою
зірок, які можна побачити через телескоп, обчислюється за формулою ![]()
![]() , де D - діаметр об'єктива телескопа в сантиметрах.
, де D - діаметр об'єктива телескопа в сантиметрах.
Деякі формули фізики в яких використовуються логарифми:
- Зв’язок між сталою розпаду , середнім часом життя і періодом піврозпаду Т
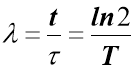
– середній час життя;
Т – період піврозпаду;
-
Рівень інтенсивності звуку. Величина рівня інтенсивності звуку рівна десятковому логарифму відношення інтенсивності досліджуваного звуку до інтенсивності на межі. І – інтенсивність звуку яка порівнюється ;
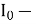 інтенсивність звуку, що береться за нульовий рівень.
інтенсивність звуку, що береться за нульовий рівень.
 ІІІ. Логарифмічна спіраль
ІІІ. Логарифмічна спіраль
Логарифмічна спіраль або ізогональна спіраль — особливий вид спіралі, що часто зустрічається в природі. Логарифмічна спіраль була вперше описана Декартом і пізніше інтенсивно досліджена Бернуллі, який називав її Spira mirabilis — «дивовижна спіраль».
Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α.
Таку криву описує рухома точка, відстань від полюса якої росте в геометричній прогресії, а кут, що описується її радіусом-вектором, - в арифметичній.
Німецький поет Йоган-Вольфганг Гете вважав: Логарифмічна спіраль є математичний символ життя і духовного розвитку».
 Розмір витків логарифмічної спіралі поступово збільшується, але їх форма залишається незмінною. Можливо, внаслідок цієї властивості, логарифмічна спіраль з'являється в багатьох зростаючих формах, подібних до мушлель молюсків і квіток соняшників.
Розмір витків логарифмічної спіралі поступово збільшується, але їх форма залишається незмінною. Можливо, внаслідок цієї властивості, логарифмічна спіраль з'являється в багатьох зростаючих формах, подібних до мушлель молюсків і квіток соняшників.

По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника.
По логарифмічних спіралях закручуються раковини молюска Nautilus, роги гірських баранів, дзьоби папуг.

 Один із павуків Епейра сплітаючи павутиння, закручує нитки навколо центра по логарифмічних спіралях
Один із павуків Епейра сплітаючи павутиння, закручує нитки навколо центра по логарифмічних спіралях

Прикладом логарифмічної спіралі є галактика Сонячної системи.

Одна з чудових властивостей логарифмічної спіралі полягає в тому, що довільний промінь, що виходить з її полюса, перетинає будь-який виток спіралі під одним і тим же кутом. Ця властивість застосовується в ріжучих машинах.

 я в ріжучих
я в ріжучих  По
По
По логарифмічній спіралі формується і тіло циклона
Логарифмічну спіраль можно побачити і в архітектурі. Наприклад, вежа Шухова в м. Москва.
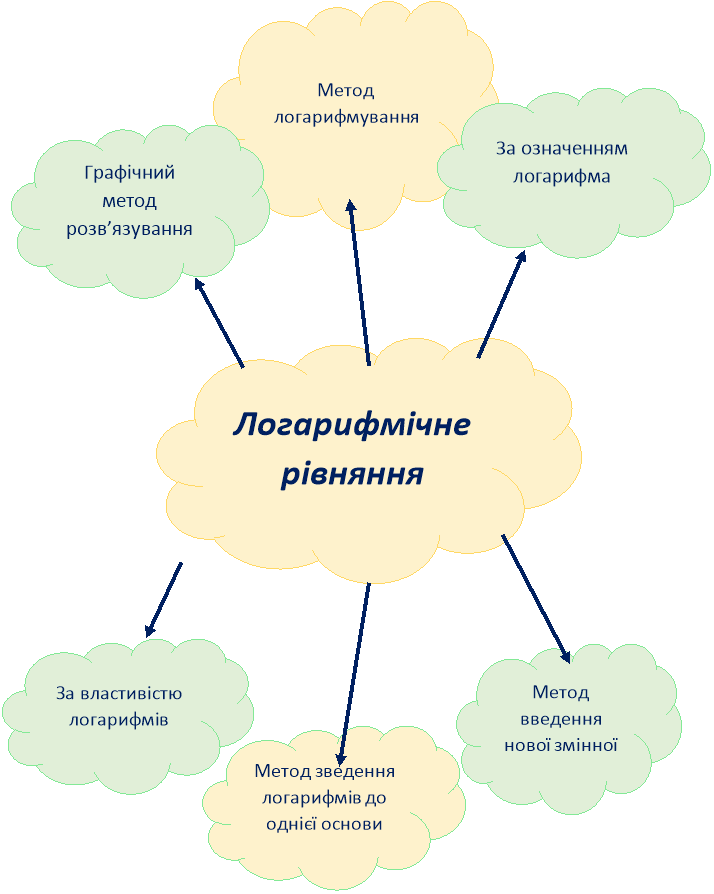
V. Встановлення відповідності «Рівняння – метод»
- Чи є існує універсальний спосіб розв’язування логарифмічних рівнянь (ні)
- Як уникнути втрату коренів та появу сторонніх коренів логарифмічних рівнянь?
Встановіть відповідність:
|
|
А |
За означенням логарифма |
|
|
2. |
|
Б |
Графічний метод |
|
3. |
|
В |
Введення нової змінної |
|
4. |
|
Г |
логарифмуванням |
|
5. |
|
Д |
За властивостями логарифма |
|
6. |
|
Е |
Зведення логарифмів до однієї основи |
VІ. Розв'язування вправ ЗНО
1.Якому проміжку належить корінь рівняння ![]() ? № 20, 2017д
? № 20, 2017д
|
А |
Б |
В |
Г |
Д |
|
(0; 2] |
(2; 4] |
(4; 6] |
(6; 8] |
(8; 10] |
Розв’язання.
![]() ;
;
ОДЗ х > 0;
![]()
![]()
![]()
Відповідь: Д
3. Розв’яжіть рівняння ![]() .
.
Якщо рівняння має один корінь, запишіть його у відповіді. Якщо рівняння має кілька коренів, запишіть у відповіді їхню суму. № 29, 2014
Розв’язання.
![]() ;
;
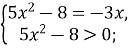 або
або ![]()
Вибір відповідної системи пов’язаний з тим, яку з нерівностей, легше розв'язати
![]()
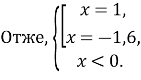
Відповідь: –1,6
Якщо рівняння має один корінь, то запишіть його у відповідь; якщо воно має два корені, то у відповідь запишіть їх суму. № 25, 2009
Розв’язання.
![]()
Дане рівняння рівносильне системі
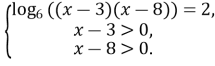
Звідси ![]()
![]()
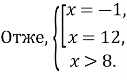
5. Розв’яжіть рівняння ![]() . Якщо рівняння має
. Якщо рівняння має
один корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то у відповіді запишіть їхню суму. Якщо рівняння не має коренів, запишіть v відповіді число 100. № 30, 2015
Розв’язання.
![]()
![]()
![]() .
.
![]()
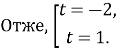
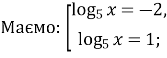
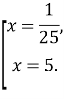
![]()
Відповідь: 5,04
Якщо рівняння має єдиний корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то запишіть у відповіді їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100. № 30, 2015
Розв’язання.
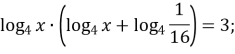
![]()
![]()
![]()
![]()
![]()
![]()
![]()
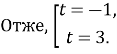
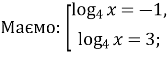
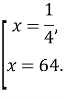
![]()
Відповідь: 64,25
VII.Підведення підсумків заняття. Рефлексія.
Інтерактивна вправа «Вимірювання температури» Перед вами на парті лежать « термометри» , зробіть справа позначку, що відповідає рівню ваших знань з теми « Логарифми, їх властивості. Логарифмічні рівняння».
Порівняйте результати
Отже, на занятті ви добре попрацювали, продемонстрували свої знання, вміння та навички, були активними.
2.Який спосіб використовувався найчастіше?
3.Який спосіб найбільше вам подобається?
4.Як уникнути втрату коренів та появу сторонніх коренів логарифмічних рівнянь?
5.З якими труднощами ви зустрілися? Що допомогло подолати ці труднощі (конспект, допомога товариша, типові приклади в зошиті …)?
6.Що на занятті було цікавим? Не цікавим?
Подарунок осінній листок із хорошими побажаннями.
VIIІ.Домашнє завдання.
Варіант 1
1. Повторити відомості про логарифмічні рівняння та методи їх розв’язування.
2. Розв’язати рівняння:
|
1) |
|
3) |
|
|
2) |
|
4) |
|
|
|
|||
3* Знайти значення виразу:
![]()
Варіант 2
1. Повторити відомості про логарифмічні рівняння та методи їх розв’язування.
2. Розв’язати рівняння:
|
1) |
|
3) |
|
|
2) |
|
4) |
|
|
|
|||
3* Створити кросворд до теми «Логарифмічні рівняння»
Урок алгебри у 11 класі. Вчитель математики Коваленко Н.М. листопад 2019


про публікацію авторської розробки
Додати розробку