Урок на тему " Розв'язування показникових рівнянь, нерівностей"
Тема . Розв'язування показникових рівнянь, нерівностей.
Мета: узагальнити та систематизувати знання і вміння учнів із теми «Показникова функція»: властивості показникової функції, способи розв'язання показникових рівнянь і нерівностей; перевірити рівень засвоєння знань учнів із теми, вміння користуватися вивченим матеріалом; розвивати активність, прагнення до пошуку оптимальних рішень, вміння швидко орієнтуватися в різних ситуаціях; формувати вміння та навички аналізувати, узагальнювати, систематизувати; сприяти активізації розумової діяльності учнів, прищеплювати любов до математики; виховувати наполегливість у досягненні мети, дисциплінованість, вміння раціонально використовувати час уроку.
Розум полягає не лише у знанні,
але й у вмінні застосовувати ці знання.
Арістотель.
ХІД УРОКУ
I. Організаційний момент
II. Постановка проблеми.
Учитель. Вітаю вас на уроці з теми «Розв'язування показникових рівнянь, нерівностей ». Сьогодні настав час вам перевірити, як ви оволоділи основними методами розв'язування показникових рівнянь та оволодіти навичками розв’язувати показникові нерівності, як можете знайти вихід із нестандартної ситуації, наскільки цінні є ваші ідеї та цікаві думки. Нині багато формалізованих задач виконує обчислювальна техніка, зокрема комп'ютер. Але зростає роль неформального, творчого мислення та вміння застосовувати здобуті знання. Тому актуально звучать слова видатного, давньогрецького вченого і філософа, що є епіграфом уроку.
На уроці вам надається можливість оцінити власні знання. У кожного на партах лежать талони самоконтролю, які ви заповнюватимете протягом усього уроку.
Талон самоконтролю
Прізвище, ім'я____
|
1 |
«Історична довідка» |
|
|
2 |
«Інтелектуальна розминка », «Дуель» |
|
|
3 |
«Домашнє завдання» |
|
|
4 |
«Практикум»
|
|
|
5 |
«Темна конячка»
|
|
|
6 |
«Ерудити» |
|
|
7 |
«Поетичний» |
|
ІІІ. Актуалізація опорних знань.
Раунд 1 «Історична довідка»
Реклама першої команди
- Вони допомогли математикам розширити область визначення показника степеня.
- За їх допомогою було узагальнено поняття степеня.
- За їх допомогою Леонард Ейлер відкрив показникові і логарифмічні кількості.
- Якщо ви хочете пов'язати своє життя з наукою, то вивчайте показникові рівняння та методи їх розв'язування.
Повідомлення
Термін “показник” для степеня ввів у 1553р. німецький математик (спочатку монах, а потім - професор) Михайль Штифель (1487-1567).По-німецьки “показник”- Exponent, з латині exponere - “виставляти на показ”; exponens, exponentis “що виставляється на показ”, “той, що показується”. Штифель увів дробові й нульові показники. Позначення ж ах для натуральних показників увів Рене Декарт (1637), а вільно поводитися з такими самими дробовими й від'ємними показниками почав з 1676 року Ісаак Ньютон. Степені з довільними дійсними показниками, без будь-якого загального означення, розглядали Лейбніц та Іоганн Бернуллі. 1679р. Лейбніц увів поняття експоненціальної (тт. показникової) функції для залежності у=ах та експоненціальної кривої для графіка цієї функції.
Питання, пов'язане з показниковою функцією, розробляв Леонард Ейлер. У двох розділах своєї праці «Вступ до аналізу» він описав «показникові і логарифмічні кількості». В ній, зокрема, зазначено, що показникові кількості можуть бути різноманітними залежно від того, «чи буде змінною кількістю один лише показник, чи, крім того, ще і кількість, які підносять до степеня». Ейлеру належить відкриття зв'язку між показниковою і тригонометричною функціями.
Реклама другої команди
- Вам треба дізнатися про радіоактивний розпад?
- Ви хочете розрахувати приріст деревини?
- Вам треба визначити зміну атмосферного тиску?
- Тоді дружіть з показниковими рівняннями! Вони допомагатимуть вам розв'язувати багато практичних проблем.
Повідомлення
У природі, техніці, економіці зустрічаються процеси, протікання яких відбувається за законом показникової функції. Ці процеси називають процесами органічного зростання або органічного згасання. Наприклад, ріст бактерій в ідеальних умовах відповідає процесу органічного зростання, радіоактивний розпад речовини — процесу органічного згасання.
Так, температура чайника змінюється з часом за формулою Т = Т0 + (100 - Т0 )е-kt
Хімічний елемент радій розпадається з часом за законом М = М0е-kt, де М0 — початкова кількість радію, к — деякий коефіцієнт. Користуючись цією формулою, вчені змогли підрахувати вік Землі.
За законом N = N0е kt , де N0 — початкова кількість деревини, k — деякий коефіцієнт, змінюється кількість деревини у дереві, що важливо для раціонального ведення лісового господарства.
Сума грошей, покладених у банк на кілька років, змінюється за законом А =А0(1 + р)t, де А0 — початкова кількість грошей, р — відсоткова ставка банку.
Раунд 2 «Інтелектуальна розминка »
Запитання команді 1.
1. 9,80 (1)
2. у=ах . При а>1 функція … (зростає)
3. ![]() (5)
(5)
4. Множина значень х, для яких визначені значення у(х), називається …
(областю визначення функції у (х))
5. Область визначення показникової функції …… ( )
6. 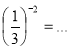 (9)
(9)
7. Метод розв'язування рівняння 3х+1 – 3х-2 = 26 (винесення спільного множника за дужки)
8.Розв'яжіть нерівність 3х < 34 (х<4)
9. 3х = 1, х = … (х=0)
10.Чи зростає функція у = (0,5)х (ні, спадає)
Запитання для команди 2
1. 3-2 = (1\9)
2. Вкажіть точки перетину графіка функції у=ах з віссю абсцис (точок перетину немає)
3. Через яку точку обов'язково пройде графік функції у = ах ? ( (0; 1) )
4. Множина значень показникової функції … (R+)
5. а>1, ах1>ах2 . Порівняйте х1 і х2 (х1 > х2)
6. Обчисліть 63 · 6-2 = ( 6 )
7. Порівняйте числа π - 3 і 1 (π -3 < 1 )
8. Метод розв’язування нерівності ( заміна 3х новою змінною і
3 · 9х + 11 · 3х – 4 < 0 зведення до квадратної нерівності )
9. 6250,5 = (25)
10. Чи зростає функція у = ( ![]() )х (так)
)х (так)
У цей час біля дошки по одному учню з кожної команди беруть участь у конкурсі «Дуель», який оцінюється в 3 бали.
Завдання для учня з першої команди.
Яке число потрібно поставити замість знака «?»
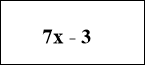



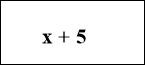
10
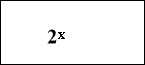
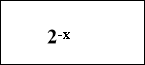
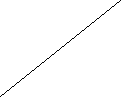

2 сos 2x

Складемо рівняння : х+5+7х- 3 = 10,
8х = 8,
х=1.
Складемо наступне рівняння:
2х + 2 –х = 2 сos 2x
Розв’язання.
Оцінимо ліву і праву частину рівняння:
2х + 2 –х = 2х + ![]() ≥ 2;
≥ 2;
2 сos 2x ≤ 2.
Замінимо рівняння рівносильною системою:
2х + ![]() = 2;
= 2;
2 сos 2x = 2.
Розв’яжемо перше рівняння системи:
2х = у;
у + ![]() = 2;
= 2;
у2 – 2у + 1 = 0;
у = 1;
2х = 1 ;
х= 0.
Перевіримо, чи задовольняє корінь х=0 друге рівняння системи :
2 сos 2∙ 0 = 2;
2 ∙ 1 = 2.
Значить, х=0 – розв’язок системи, отже і даного рівняння.
Відповідь : 0 .
Завдання для учня з другої команди.
Яке число потрібно поставити замість знака «?»
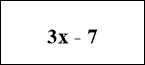


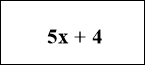

13
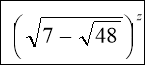




14
Складемо рівняння : 3х - 7+5х + 4 = 13,
8х = 16,
х=2.
Складемо наступне рівняння:
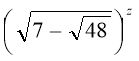 +
+ 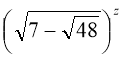 = 14
= 14
Відповідь : z = ± 2
Раунд 3 «Домашнє завдання»
Кожна група (трійка) готуючись до уроку, отримала завдання вибрати найзручніший спосіб розв’язування запропонованого показникового рівняння.
Група «1»
Спосіб зведення до спільної основи.
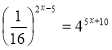
![]()
-2(2х - 5) = 5х+10
-4х+10 = 5х+10
-9х = 0
х = 0
Відповідь : 0
Група «2»
Спосіб зведення до спільного показника.
2х+3 ∙ 3х = 288
2х ∙ 23 ∙3х = 288
2х ∙ 3х = 288 : 8
(2∙3)х = 36
6х = 62
х = 2
Відповідь : 2
Група « 3 »
Спосіб зведення до квадратного рівняння.
4х – 12 ∙ 2х + 32 = 0
22х – 12 ∙ 2х + 32 = 0
2х = а
а2- 12а + 32 = 0
а1+а2 = 12
а1 ∙ а2 = 32
а1 = 8
а2 = 4
2х = 8 2х = 4
2х = 23 2х = 22
х=3 х=2
Відповідь : 2 ; 3.
Група «4»
Спосіб винесення спільного множника за дужки
2х+1 + 5 ∙ 2 х-2 = 104
2х ∙ 2 + 5 ∙ 2х ∙ ![]() = 104
= 104
2х ( 2 + ![]() ) = 104
) = 104
2х ( ![]() ) = 104
) = 104
2х ∙ ![]() = 104
= 104
2х = ![]()
2х = 32
2х = 25
х = 5
Відповідь.
Група «5»
Спосіб групування множників.
20 3х+2 = 4х+12 ∙ 55х – 8
(5 ∙ 4)3х+2 = 4х+12 ∙ 55х – 8
53х+2 ∙ 43х+2 = 4х+12 ∙ 55х – 8 / : 43х+2
53х+2 = 4 х+12 -3х-2 ∙ 55х – 8
53х+2 = 4 10 - 2х ∙ 55х – 8 / : 55х – 8
53х+2 – 5х+8 = 4 10 - 2х
510 – 2х = 4 10 - 2х / : 510 – 2х
1 = 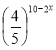
![]() =
= 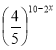
10-2х = 0
2х = 10
х = 5
Відповідь : 5
Висновок : побудова асоціативного куща до математичного поняття «показникові рівняння»


![]()




![]()
![]()
![]()
![]()


Раунд 4 «Практикум»
- Ви проілюстрували свої вміння розв’язувати показникові рівняння різними способами, час переходити до розв’язування показникових нерівностей.
Алгоритм
- Зведемо обидві частини нерівності до спільної основи.
- Встановимо : чи є функція зростаючою чи спадною.
- Враховуючи монотонність функції з даною основою, складемо нерівність із показників степенів.
- Розв'яжемо одержану нерівність.
- Запишемо відповідь
- Колективне розв’язування вправ.
Розв’язати нерівність.
![]() <
<![]() <0,5
<0,5
![]() >
> ![]() > 1
> 1
1 <![]() <
<![]()
1 < ![]() <
<![]()
1 <![]() <
<![]()
1 < сtg x <![]()
![]() + πn < x <
+ πn < x < ![]() + πn, n
+ πn, n ![]() Z.
Z.
Раунд 5. «Темна конячка»
Розв'яжіть самостійно рівняння та нерівності і розшифруйте слово
Команда 1 .
1.Розв'язати рівняння
4х – 3 ·2х = 40.
Відповідь : 3
2. Розв’язати нерівність
4![]() < 8.
< 8.
Відповідь: (- 0,5 ; 2,5)
Команда 2 .
1.Розв'язати рівняння
![]() + 3х + 3 = 12.
+ 3х + 3 = 12.
Відповідь : - 2
2. Розв’язати нерівність
2х + 21-х ≤ 3
Відповідь : [ 0; 1]
|
3 |
-2 |
(0 ; 1] 1) |
( - 0,5 ; 2,5) 2,5) |
||
|
В |
І |
Т |
А |
Ю |
! |
Раунд 6 «Ерудити»
Завдання для першої команди

![]()
у = 0,5 ![]() + 8 · 0,5
+ 8 · 0,5 ![]() + 15,
+ 15,
![]()
Відповідь : [0; ∞) (розв’язати нерівність 0,5 ![]() + 8 · 0,5
+ 8 · 0,5 ![]() + 15 ≥0 )
+ 15 ≥0 )
Завдання для другої команди
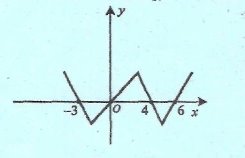
![]()
у = 3![]() + 3
+ 3 ![]() - 3
- 3![]() - 11,
- 11,
![]()
Відповідь : [0; 4) (розв’язати нерівність 3![]() + 3
+ 3 ![]() - 3
- 3![]() - 11 < 0)
- 11 < 0)
Раунд 7
Це естафета, у якій беруть участь по 7 учнів від кожної команди. Кожний крок оцінюється одним балом.
Завдання для першої команди
Побудувати графік функції :
у = 3 ![]() - 1
- 1
Відповідь.
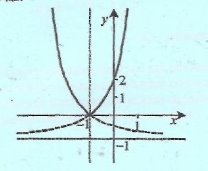
Завдання для другої команди
Побудувати графік функції :
у = 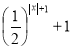
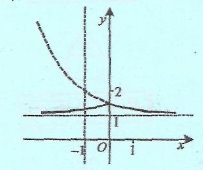
Відповідь.
Раунд 7 «Поетичний» (Підсумок уроку)
Кожна команда повинна скласти сенкан про показникові рівняння.
Перша команда
Показникові рівняння.
Гарні, потрібні.
Розв'язуємо, мислимо, застосовуємо.
Розв'язуємо з великим задоволенням.
Друга команда
Показникові рівняння.
Важливі, захоплюючі.
Розв'язувати, думати, розбирати.
Розв'язуємо рівняння для тренування.
- Домашнє завдання. Завдання для самоперевірки № 5 ст. 234 - 236
- В.Кравчук “ Алгебра і початки аналізу ”


про публікацію авторської розробки
Додати розробку
