Урок "Задачі з параметрами".

Задачі  з параметрами.

Якщо запастися терпінням і проявити старання,

то посіяне насіння знання неодмінно дасть добрі сходи.

Леонардо да Вінчі

Мета: Розширити знання учнів з теми «Рівняння, нерівності та їх системи», вчити застосовувати набуті знання, розвивати логічне мислення, практичні навички у нестандартних ситуаціях, формувати математичні компетентності.

Тип уроку: урок-практикум.

Зміст уроку:

 «Не кажи — не вмію, а кажи — навчусь!»

І. Актуалізація опорних знань(«Асоціативний кущ»)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ. Сьогоднішній урок спрямований на розширення ваших знань з теми «Рівняння, нерівності та їх системи». В ДПА – 30% завдань – розв’язування рівнянь, нерівностей та їх систем; в ЗНО – 18,75% рівняння і нерівності, 18,75% – функції та їх властивості тобто майже 40%.  Як правило, задача з параметром – це завдання, яке оцінюється найбільшою кількістю балів в ДПА та ЗНО, тобто «коштує» найдорожче. Тож сьогодні ми будемо збирати дорогоцінні камінчики в скарбничку ваших знань. У кожного з вас є вже відома вам картка успіху (таблиця результатів), заповнюйте її протягом уроку а  останню колонку (самостійну роботу) оціню я і поставлю загальну оцінку за урок.

Підсумуємо вище сказане

Запитання до класу («Незакінчене речення»):

1. Якщо рівняння, крім змінної містить невідоме… (то його називають рівнянням з параметром)
2. Параметр це -  …(незалежна змінна, значення якої є фіксоване чи довільне дійсне число, або число, що належить заданій множині)
3. Методи розв’язування задач з параметрами …(графічний та аналітичний)
4. Розв’язати задачу з параметром – це знайти …(значення змінної для всіх значень параметра )
5. Основними типами задач з параметрами є …(знайти кількість розв’язків, розв’язати для будь-якого а, знайти всі значення, які задовольняють умову)

“Очі бояться – руки роблять.”

ІІ. Формування в учнів уміння розв’язувати задачі з параметрами:

  Необхідно пам’ятати:

Аналітичний спосіб -  універсальний, але найбільш складний, і потребує високої математичної грамотності.

Графічний – виключно красивий і наочний але не завжди доречний і потребує мистецтва роботи з графіками.

Читай уважно умову! І вибір за тобою! На екрані  ви бачите 2 задачі. Яким способом ви б розв’язували 1? А другу? (2 учні до дошки)

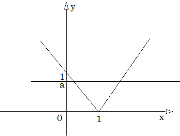
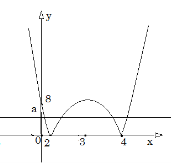
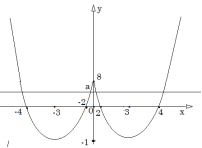
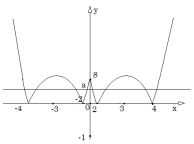
 А ми разом попрацюємо усно. Увага на екран. Яку найбільшу кількість розв’язків має рівняння в залежності від параметра а.(Розв’язуємо графічно)

 

№	Рівняння	Графічне розв’язання
1		2
2		4
3		4
4		8
5		8

  

(3) Виконання вправ:

Рівняння

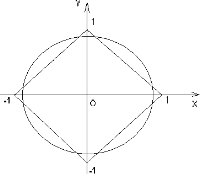
№1 При якому значенні а рівняння має більше 2-х коренів?

 

 

 

 

 

 

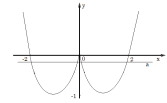
Відповідь:

 

№2 Знайдіть всі значення параметра а  при якому всі точки екстремуму функції

у = х³ - 3ах² +3(а² +1)х – 4  належать проміжку

Розв’язання

Згадаємо як знайти точки екстремуму функції (точки в яких похідна =0 або не існує)

у^/  = 3х² - 6ах +3(а² +1)

х² - 2ах +(а² +1)=0

х = а ±1

→ →

 

Відповідь:

 

«Один розум добре, а два ще краще!»

Ще один тип рівнянь. Це рівняння, що зводяться до квадратних. (Робота в парах.)

№3  При якому значенні а рівняння + 4а – 12 = 0 має 1 корінь?

Розв’язання

Р-ня зводиться до квадратного.

D= а² – 14а + 49 = (а - 7)²

 при а=7 =4 (тобто корені однакові)

                                          (другий корінь не існує)

 

Отже рівняння матиме 1(2 однакових) корінь х=1 при а=7 або якщо рівняння не має коренів тобто при а ≤ 3

Відповідь: а

 

«Добрий початок — половина діла.»

В ДПА часто зустрічаються ірраціональні нерівності. Давайте разом розв’яжемо одну з них.

№4 Нерівності

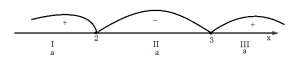Розв’яжіть нерівність для всіх значень параметра а.

ОДЗ:

Один з множників = 0 або обидва додатні

 

 

Відповідь:І -  якщо

                   ІІ -  якщо

     ІІІ - якщо

А якщо поміняти місцями ( «Лови помилку»)

   (малюнок той же)

ОДЗ:

Один з множників = 0 або обидва додатні

Відповідь: І -  якщо

                  ІІ -  якщо

     ІІІ - якщо

 

 «Не такий страшний чорт, як його малюють.»

№5 Системи рівнянь. (Евристична бесіда)

Найчастіше зустрічаються 2 типи завдань:

1. при яких значеннях а система не має (має безліч) розв’язків;
2. при яких значеннях а система має задану кількість розв’язків.

Перший випадок

Наприклад:

Для лінійних систем:

безліч розв’язків – це повна пропорція відповідних коефіцієнтів   ;

немає розв’язків – це коли останнє відношення ≠ першим двом   

У другому випадку система найчастіше розв’язується графічно (беруть участь кола або квадрат)

- - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Наприклад:

При якому значенні а система рівнянь має єдиний розв’язок?

 

 

 

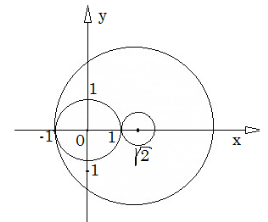
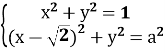
Два кола, що дотикаються (зовнішньо або внутрішньо)

для великого кола :

а² =  

а= або а=

для малого кола :

а²  =  

а= або а=

Найменше з них а=

 

Відповідь: а=

 

                                                                                                        ІІІ. Самостійна робота

А зараз попрацюємо самостійно. Виберіть завдання вам по силам.

 

Д/З

Підберіть і розв’яжіть 1 рівняння, 1 систему, 1 нерівність з параметром (з завдань ДПА 4 рівня 4.1), або з завдань 3 рівня(по 2).

 

 

Картка успіху

П.І.	Бачити помилку	Проаналізувати умову	Запропонувати крок розв’язування	Аргументувати	Запропонувати спосіб розв’язування	Відповісти на запитання	Самостійна робота

 

Мої враження про урок

+ Плюс	Мінус	?!! Цікаво

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додатки

 

№1 При якому значенні а рівняння  має більше 2-х коренів?

 

 

 

№2 Знайдіть всі значення параметра а  при якому всі точки екстремуму функції

у = х³ - 3ах² +3(а² -1)х – 4  належать проміжку

 

 

 

 

№3 При якому значенні а рівняння + 4а – 12 = 0 має 1 корінь?

 

 

 

 

№4 Нерівності

Розв’яжіть нерівність для всіх значень параметра а.

 

 

 

№5 Системи рівнянь.

При якому значенні а система рівнянь має єдиний розв’язок?