Урок "Ознаки паралельності прямих"

                                       Урок №                                                                         -----------------

Тема: Ознаки паралельності прямих

Мета: закріпити знання учнів про ознаки паралельності двох прямих (за кутами, що утворилися при перетині даних прямих січною).

Сформувати вміння:

-         Визначити вид двох кутів, що утворилися при перетині двох прямих січною;

-         За певним співвідношенням цих кутів робити висновок щодо паралельності прямих;

-         Для встановлення співвідношення кутів використовувати знання про властивості кутів (вертикальних, суміжних, при основі рівнобедреного трикутника).

Тип уроку: застосування знань, застосування вмінь та навичок.

Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця «Ознаки паралельності прямих»

                                                       Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

Математичний диктант

1. Накресліть дві прямі та січну. Позначте всі кути, що при цьому утворилися. З позначених кутів виберіть та запишіть:

а) усі пари внутрішніх односторонніх;

б) усі пари внутрішніх різносторонніх;

в) усі пари відповідних кутів.

2. Закінчіть речення: « Дві прямі, паралельні третій…»

3. Прямі p I c перетнуті січною так, що сума внутрішніх односторонніх кутів становить 200. Скільки спільних точок мають прямі p I c?

4. Паралельність яких прямих на рисунку 1 випливає з того, що = 3? Поясніть свою думку.

 A B

 M K

ІІІ. Мотивація навчальної діяльності. Формування мети й завдань уроку.

Задача. На рисунку 2 АВ=ВС, АС- бісектриса кута ВАD. Доведіть, що ВС||АD.

Розв’язання. За умовою задачі трикутник АВС рівнобедрений з основою АС. За властивістю  кутів рівнобедреного трикутника 1=3. Разом із тим 1=2, оскільки АС – бісектриса кута ВАD. Звідси 2=3. Кути 2 і 3 є внутрішніми різносторонніми при прямих АD і ВС та січній АС. Оскільки ці кути рівні, то  за ознакою паралельності прямих АD||BC, що й треба було довести.

ІV. Актуалізація опорних знань

Виконання усних вправ

1. На рисунку 3 назвіть пари:

а) внутрішніх різносторонніх кутів при прямих АD, МЕ і січній ВО;

б) внутрішніх односторонніх кутів при прямих АD, МЕ і січній КС.

2. а||b. Чи правда, що b||a?

3. Чому дорівнює сума внутрішніх односторонніх кутів, якщо:

а) внутрішні різносторонні кути рівні;

б) відповідні кути не рівні?

4. Скільки прямих, паралельних даній, можна провести через точку, що не лежить  на даній прямій?            S

               Р C D

А В

E

       М О K

                                R                 Q

V. Засвоєння вмінь

1. Прямі а і b перетинають пряму с під рівними кутами . Чи обов’язково а||b?

2. За даними рисунка 5 доведіть, що а||b .

              c

а      25

   b

 25

2. На рисунку 6 АВ=ВС, СD=DE. Доведіть, що АВ|| DE.

                              В

           А

 С E

                                          D

3. На рисунку АD = CF, ВС=DE, 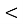1=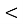2. Доведіть , що АВ || EF.

 1 2

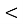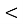4. У трикутнику АВС А=20, В=80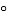. Із точки В проведено промінь ВD так, що ВС – бісектриса кута АВD. Доведіть , що АС||BD.

VI. Підсумки  уроку.

Складаємо алгоритм доведення паралельності двох прямих.

VII. Домашнє завдання

Повторити ознаки паралельності прямих.

1. За рисунком визначте, чи паралельні прямі а і b, якщо:

а) 5=35, а 4 втричі більший, ніж 3;

б) 2=72, а 6:8=2:3

 c

 a               7       8

                                                 5        6

 b 3      4

 1 2

2. Відрізки АВ і СD перетинаються в точці, яка є їхньою спільною серединою. Доведіть, що АС||BD.