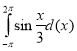Урок "Площа криволінійної трапеції"
Інтегрований урок з фізичною культурою, метою якого є творче поєднання знань і вмінь з теми “Інтеграл "та спортивних досягнень українських спортсменів на ХХІІ зимових Паралімпійських іграх.



( Інтегрований урок з фізичною культурою)
Показовий урок,
проведений в 11 класі
учителем математики
Липівської ЗОШ І-ІІІ ст.
Динник Л.Г.
Тема: Розв'язування вправ на обчислення площі криволінійної трапеції
Мета уроку: закріпити поняття криволінійної трапеції, визначеного інтеграла; закріпити уміння застосовувати формулу Ньютона-Лейбніца та властивості інтеграла до обчислення визначених інтегралів; формувати уміння учнів застосовувати інтеграл до обчислення площ плоских фігур; розвивати логічне мислення, обчислювальні навички, увагу, пам'ять; виховувати інтерес до математики, згуртованість, повагу до товаришів та їхньої думки, почуття патріотизму, гордості, любові до спорту та рідної України.
Тип уроку: урок творчого застосування знань і вмінь з підтримкою ІКТ.
Обладнання: картки з індивідуальними завданнями, комп’ютерна презентація за програмою Pоwer Point, комп’ютерні тести, екран , проектор, комп’ютери.
Епіграф
"Важливо не те, що загублено, важливо те, що залишилося”
Людвіг Гутман

Девіз уроку
Через терни інтегралів,
Через первісних таблиць,
Ми рахуємо уміло ,
Площ трапецій непростих.
І. Пропедевтична практика
Мотивація навчальної діяльності
Сьогодні на уроці ми повторимо, узагальнимо знання і вміння, набуті під час вивчення теми “Інтеграл ”. Щоб виконати запропоновані завдання, які буде подано в нестандартній формі, ви повинні скористатися раніше вивченим матеріалом, проявити творчі здібності та уміння працювати самостійно і в колективі.
Це не простий урок математики, а урок інтегрований з фізичною культурою. Слово «інтеграція» означає об’єднання в ціле раніше ізольованих частин. Спробуємо об’єднати математику із один із напрямків фізичної культури..
Та спочатку перевіримо домашнє завдання і визначимо, яка тема з фізичної культури нас зацікавить на уроці.
(На екрані показано правильне виконання домашнього завдання. Учні перевіряють правильність виконання в зошиті сусіда по парті. Олівцем виставляють оцінки. На екрані поряд з кожним завданням записана літера алфавіту та відповідна кількість балів.) ( слайд )
|
|
|
y=x2-4x+5, y=5 S-? |
|
|
|
6,6 |
3 |
10 |
|
|
|
С |
П |
О |
Р |
Т |
Фізкультура направлена на зміцнення здоров’я, а спорт направлений на одержання максимального результату і спортивних нагород. Але в широкому розумінні сучасне поняття фізичної культури включає в себе тільки ті види спорту, які направлені на виконання певних фізичних вправ і високої рухомої активності.
Так, ми сьогодні поговоримо про спортивні змагання, а точніше про паралімпійські змагання.
З 9 березня по 18 березня 2018 року проходили ХХІІ зимові Паралімпійські ігри у Пхьончхані Південної Кореї. 19 березня наші параолімпійці повернулися додому високо піднявши прапор України. Вони прославили нашу країну на весь світ своїми здобутками.

Але перш ніж розпочати перегляд паралімпійського щоденника пригадаємо основні теоретичні факти про інтеграл. Давши вичерпні відповіді ви дізнаєтесь що є графічним символом світового паралімпійського руху. ( Слайд )
2. Актуалізація опорних знань.
Проводиться у формі фронтального опитування як інтерактивна вправа “Мікрофон”
1. Що називається інтегруванням? диференціюванням?
(Знаходження функції f(x) за її заданою похідною f1називається операцією інтегрування. Операція знаходження похідної називається диференціацією)
2. Що називається первісною функції?
(Функція F(x) називається первісною для функціїf(x) на даному проміжку, якщо для будь-якого x із цього проміжку F!(x)=f(x))
3. Хто ввів термін первісна у математику?
(Жозеф Луї Лагранж у 1797 році).
4. В якому році вчений Якоб Бернуллі ввів термін «Інтеграл»?
(1690 – рік , в якому Якоб Бернуллі ввів термін «Інтеграл»)
5. Що називається невизначеним інтегралом функції?
(Сукупність усіх первісних для даної функції f(x) називають невизначеним інтегралом і позначають символом ![]() одна з первісних функції f(x), C – довільна стала.)
одна з первісних функції f(x), C – довільна стала.)
6. Хто ввів символ ![]() і поняття невизначеного інтеграла?
і поняття невизначеного інтеграла?
(Готфрід Вільгельм Лейбніц у 1675 році).
7. Що є криволінійною трапецією?
(Фігуру, обмежену графіком функції y=f(x), відрізком [a;b] осі Ох і прямими x=a I x=b називають криволінійною трапецією.)
8. Що називається визначеним інтегралом?
(Різниця F(b)-F(a) називають визначеним інтегралом функції f(x) на відрізку[a;b] і позначають 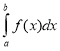
9. Запишіть формулу Ньютона – Лейбніца.
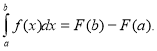
10. Хто ввів позначення 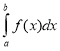 в математику?
в математику?
(Жан Батист Жозеф Фур’є у 1799 році).
Отже, графічним символом світового параолімпійського руху стали червона, синя і зелена півсфери, що символізують розум, тіло, непокірливий дух.
- ІІ. Орієнтація
Виникнення видів спорту, в яких можуть брати участь люди з інвалідністю, пов'язують з ім'ям англійського нейрохірурга Людвіга Гутмана, який, долаючи вікові стереотипи по відношенню до людей з фізичними порушеннями, увів спорт у процес реабілітації пацієнтів з ушкодженнями спинного мозку. Він на практиці довів, що спорт для людей з інвалідністю створює умови для успішної життєдіяльності, відновлює психічну рівновагу, дозволяє повернутися до повноцінного життя.
А ми розв’язавши усні вправи доведемо своє уміння застосовувати теоретичні знання до знаходження площі криволінійної трапеції. (Слайди )
![]()
![]()
![]()
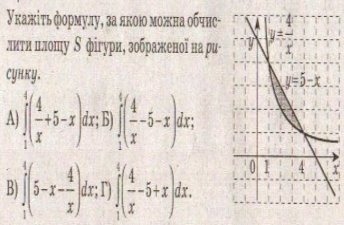
Цього року українську збірну представили 30 спортсменів: 20 з них брали участь у змаганнях, ще 10 – їхні спортсмени-лідери, які допомагали спортсменам стартувати і пересуватися трасою.
Як називають спортсменів-лідерів? На це запитання ви отримаєте відповідь знайшовши відповідність між фігурами та їх площами.
![]()

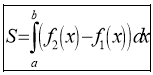
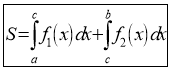
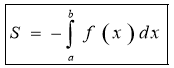
Гайд - спортсмен, який веде по трасі паралімпійця з порушенням зору. Він забезпечує при виступі у парі зі спортсменом з інвалідністю по зору виконання ним тренувальних і змагальних завдань відповідно до плану підготовки та правилами спортивних змагань, забезпечує його старт, а під час проходження дистанції керує діями, у тому числі із застосуванням радіозв'язку, і забезпечує фініш.
Українці на Паралімпіаді-2018 у Пхьончані, як і завжди показали прекрасні результати. Після завершення всіх завдань наша збірна розмістилася на шостому місці у медальному заліку.

От і ви зараз продемонструєте свої результати під час перевірки рівня знань
відповівши на 12 тестових запитань.
Комп’ютерний тест
Програма MyTest (учні працюють за комп’ютерами) (слайд
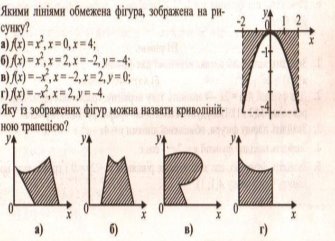
1. На якому рисунку фігура не є криволінійною трапецією?
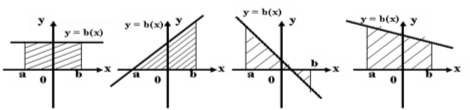
- a;
- б;
- в;
- г;
- на усіх рисунках - криволінійна трапеція.
2. Знайдіть загальний вигляд первісної для функції
f(x)= 4x![]() -9x
-9x![]() +1
+1
-
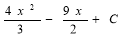
-
12x
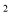 -38x+C
-38x+C
-
x
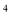 -3x
-3x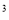 +x+C
+x+C
-
16x
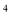 -27x
-27x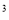 +x+C
+x+C
-
x
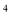 -3x
-3x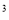 +C
+C
3. Знайдіть загальний вигляд первісної для функції:
f(x)=6x![]()
4. Обчисліть:
3
х3dx
1
- 18;
- 16;
- 20;
- 5;
- 10.
5. 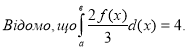
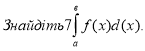
-
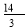 ;
;
-
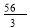 ;
;
-
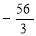 ;
;
- - 42;
- 42.
6. Для даної функції f(x)=![]() знайдіть первісну, графік якої проходить через точку А(0,1).
знайдіть первісну, графік якої проходить через точку А(0,1).
-
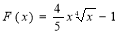 ;
;
-
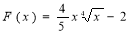 ;
;
-
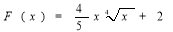 ;
;
- інша відповідь.
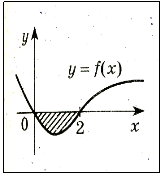
7. Знайдіть площу криволінійної трапеції зображеної на рисунку
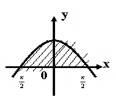
- 1;
- 2;
- π;
- інша відповідь;
- 2,5.
8. Знайдіть площу заштрихованої фігури, зображеної на рисунку
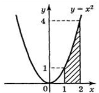
- 21/3;
- 2;
- 1/3;
- ½;
- 31/3.
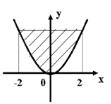
9. Який вираз дорівнює площі фігури,зображеної на рисунку:
10. Обчисліть площу фігури, обмеженої лініями у=6х![]() , у=0, х=-1, х=0
, у=0, х=-1, х=0
- 3;
- 12;
- 6;
- 9;
- 2.
11. Установіть відповідність між заданими функціями (1-4) та їхніми значеннями (А-Д).

![]()
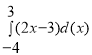 8
8

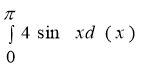
![]()
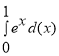 -28
-28
![]()
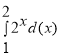 4
4
![]() e-1
e-1
12. Установіть відповідність між заданими фігурами (1-4) та формулами для обчислення їхніх площ (А-Д)
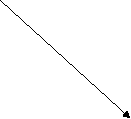

![]()
![]()
![]()
![]()
![]()
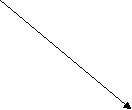
![]()
![]()
![]()
![]()
![]()
ІІІ. Керована практика
Паралімпійські ігри у Південній Кореї - шості Зимові параолімпійські ігри, в яких взяла участь Україна. Із часів нашої першої Зимової Паралімпіади в Нагано у 1998 році, українська збірна завоювала 112 медалей, 27 з яких – золоті. Найбільш успішною для наших спортсменів стала Зимова Паралімпіада -2006 у Турині – тоді Україна посіла третє місце в загальному медальному заліку, здобувши 7 золотих медалей, 7 срібних і 9 бронзових.
Відтак, на ХІІ зимових Паралімпійських іграх Україну представляла команда складом у 30 спортсменів - 11 спортсменів з ураженнями опорно-рухового апарату та 9 – з ураженнями зору; а також серед спортсменів-паралімпійців – 6 жінок та 14 чоловіків. Середній вік команди – 29 років; найдосвідченішому спортсмену - Лук'яненко Віталію – одразу після Паралімпіади-2018 виповниться 40 років; наймолодшому спортсмену Радю Тарасу – 18 років.

За дев'ять днів змагань спортсмени розіграли 80 комплектів медалей
Таким чином у скарбничці України за підсумком усіх змагань 22 медалі: 7 золотих, 7 срібних і 8 бронзових.
Продемонструємо наші досягнення при роз’язування задач на знаходження площ криволінійних трапецій.
Задача 1.
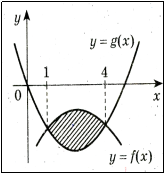
Обчисліть площу криволінійної трапеції, обмеженої графіком функції та прямими у = 0, х = 1, х = 4 .
Розв’язування
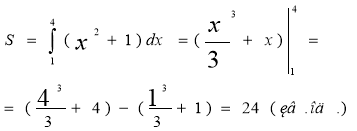
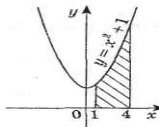
Задача 2.
Розв’язування
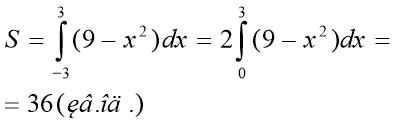
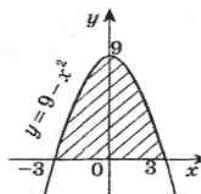
ІV. Незалежна практика
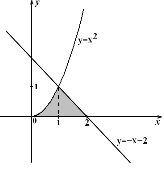
Задача 3( І рівень)
Обчисліть площу фігури за даними, поданими на рисунку.
Розв’язання
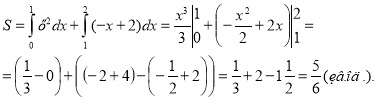
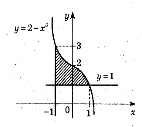
Задача 4(ІІ рівень)
Знайти площу заштрихованої фігури
Розв'язання:
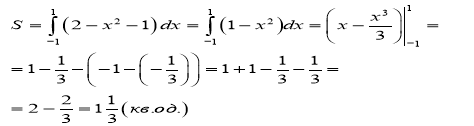
Додатково
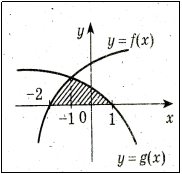
Знайти площу фігури, обмеженою лініями ![]()

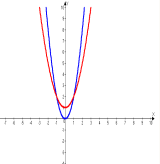
Розв’язування
1. Заштрихуйте площу фігури, яку потрібно знайти.
2. Знайдемо абсциси точок перетину графіків розв’язавши рівняння:
2х2= х2+1
х2=1
х=±1.
3. Отримана фігура симетрична відносно вісі ОY, тому площу знайдемо за формулою:
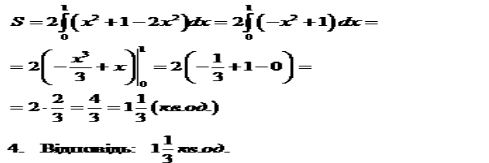
V.Домашня самостійна практика
1 варіант. Вибрати правильний варіант і обчислити площу заштрихованої фігури:
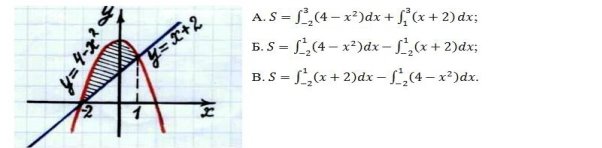
2 варіант. Знайти площу фігури, обмеженої лініями: y=x2 та y=2x+3.
3 варіант. Знайти площу фігури, обмеженої лініями : y=x2, y=2x+3 та y=0.
ЛІТЕРАТУРА
1. Мерзляк А.Г., Полянський В.Б., Якір М.С. Алгебра: підручник для загально освіт. навч зал. – Х.: Гімназія, 2008. – с. 91-108.
2. Нелін Є. П., Долгова О.Є. Алгебра: Алгебра: 11 клас: підручник для загально освіт. навч зал. – Х.: Гімназія, 2011. – с. 372-379.
3. Лосовська З.а. На урок – із сучасними інформаційно-комукаційними технологіями.- Математика в школах України, 2014, №28-29. – с. 7-12.
4. Роганін О.М. Алгебра і початки аналізу: 11 клас: Плани-конспекти уроків.- Х.: Світ дитинства, 2002. - с. 141-149.
5. Сухарева Л.С.Завдання для усної роботи, математичні диктанти та тести. Алгебра та початки аналізу. 10-11 клас. – Х.: Вид. група "Основа": "Тріада+" 2008.- с. 146-166
6. Цуренко С.П. Багатоваріантні самостійні та класні і домашні контрольні роботи: тематичне оцінювання. – Тернопіль: навчальна книга – Богдан, 2011.- с.30-33.
7. Карпінська І.Й. Нестандартні уроки з математики. – Тернопіль: Підручники і посібники, 2000. – 48 с.
8. Жумик Л.В. Інтерактивні технології навчання на уроках математики. Математика в школах України, 2006, №9. – с. 2-6.
8. Істер О. Усні вправи з алгебри та геометрії. 11 клас. – Тернопіль: Підручники і посібники, 2002. – с. 22-23.
9. Рисинець Г. Групова форма навчання. Математика, 2006, №31. – с. 19-21.


про публікацію авторської розробки
Додати розробку