Урок. Площа криволінійної трапеції. Визначений інтеграл. Формула Ньютона-Лейбніца

Методична розробка уроку

Клас 11

Предмет  Алгебра

Тема уроку  Площа криволінійної трапеції. Визначений інтеграл. Формула Ньютона-Лейбніца

Мета уроку  Познайомити учнів із задачами, які приводять до поняття інтеграла, зокрема із задачею про площу криволінійної трапеції; формувати вміння обчислювати площу фігури, обмеженої лініями; розвивати абстрактне мислення, пам’ять, увагу; впровадження технології навчання у співробітництві; взаємодіяти в групі з будь-яким партнером або партнерами; чемно і доброзичливо спілкуватися з партнерами; виховувати почуття відповідальності не тільки за власні успіхи, але й за успіхи своїх партнерів; усвідомлювати що спільна робота в групах – це серйозна і відповідальна праця; виховувати наполегливість, працьовитість, акуратність

“Учітеся, брати мої, думайте, читайте”
Т. Шевченко

Хід заняття

І. Перевірка домашнього завдання у вигляді математичного диктанту. Слайди (1-6)

Виберіть на вашу думку правильну відповідь

1. Знайдіть загальний вигляд первісних для функції .

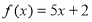А) 5+С;   Б) ;    В) ;    Г) .

2. Знайдіть загальний вигляд первісних для функції .

А) ;   Б) ;    В) ;    Г)

3. Знайдіть загальний вигляд первісних для функції .

А) ;    Б) ;     В) ;     Г)

4. Знайдіть загальний вигляд первісних для функції .

А) ;    Б) ;      В) ;     Г) .

5. Для функції знайдіть первісну, графік якої проходить через точку А(0;1).

А) ;    Б) ;     В) ;     Г) .

6. Для функції знайдіть первісну , якщо .

А) ;    Б) ;    В) ;     Г) .

Обмінялися зошитами, перевіряємо математичний диктант з коментарями. Технологія знайди помилку на дошці, відповіді обґрунтовуємо.

Слайд .Відповіді до математичного диктанту.

1. В.  2.А.   3.Г.  4. Б.  5. Б.  6. В.

2. Криволінійна трапеція.

 Формулювання теми, мети уроку.

Слайд 7

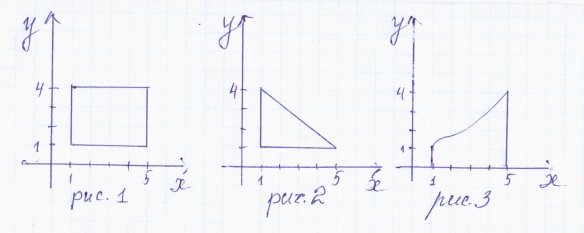
 Приклад 1. Знайдіть площу заштрихованої фігури.

• Яка фігура зображена на першому рисунку? Як обчислити її площу?
• Яка фігура зображена на другому рисунку? Як обчислити її площу?
• Виникає питання як зобразити фігуру обмеженою довільною лінією?
• Сьогодні ми познайомимося з новою для вас фігурою – криволінійною трапецією та навчимося обчислювати її площу.

Слайд 8

Криволінійною трапецією називають фігуру, обмежену графіком  неперервної функції , що не змінює знак на відрізку  прямими   і    та відрізком , який називається основою криволінійної трапеції.

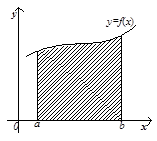• рис. 4

3. Визначений інтеграл, його геометричний зміст. (доповіді учів)

Розглянемо підхід до обчислення площі криволінійної трапеції. Для зручності вважатимемо функцію і неперервною на відрізку . Тоді площу відповідної криволінійної трапеції можна обчислити в такий спосіб.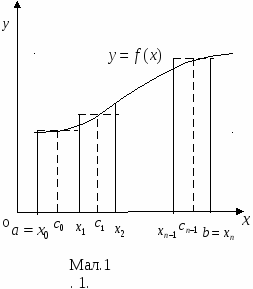

Розіб’ємо відрізок  довільним чином на  рівних частин. Точки поділу позначимо:  З цих точок проведемо перпендикуляри до перетину з кривою 

Довжини всіх відрізків, на які розбито відрізок однакові і дорівнюють . Побудуємо на кожному з відрізків к на основі прямокутники з висотою . Площа кожного такого прямокутника дорівнює , а площа ступінчатого многокутника утвореного всіма прямокутниками, дорівнює сумі площ прямокутників:

.

При , а оскільки функція неперервна, то площа ступінчатого многокутника при буде дедалі менше відрізнятися від . Отже, за площу криволінійної трапеції ми приймаємо границю площі ступінчатого многокутника при умові що , тобто . Отже, при .

Більше того, для будь-якої неперервної на відрізку функції (не обов’язково невід’ємної) при прямує до деякого числа. За означенням це число називають визначеним інтегралом функції
від до і позначають 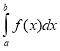, тобто при .

Числа і називають межами інтегрування: - нижня межа, - верхня межа. 

Символ називають знаком інтеграла, цей знак нагадує розтягнуту букву (у давнину його часто використовували для позначення суми).

Функцію називають підінтегральною функцією, а змінну

- змінною інтегрування.

 Отже, якщо на відрізку , то площа відповідної криволінійної трапеції виражається  формулою 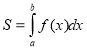, а ми знаємо, що .

4. Формула Ньютона- Лейбніца.

(застосовуємо метод «навчання в команді» під назвою «Вчимося разом» ст. 102-110 С. Сисоєва «Інтерактивні технології  навчання дорослих»;  учні розповідають про формулу Ньютона-Лейбніца, головна ідея – вчитися разом, а не просто щось виконувати разом, метод навчання у співробітництві відповідає ідеології особистісно орієнтованого навчання)

Якщо - первісна для функції на відрізку , то 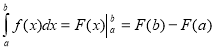. Цей вираз називається формулою Ньютона-Лейбніца. Вона справедлива для будь-якої функції , неперервної  на відрізку .

Для зручності різницю прийнято позначати скорочено , тобто 

Тоді формула Ньютона-Лейбніца матиме вигляд .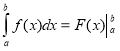

Слайд 9

Приклад 3. Обчисліть .

.

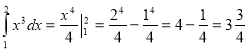Слайд 10

Приклад 4. Обчисліть .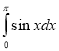

.

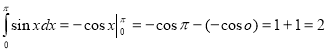Слайд 11
Приклад 3.  Обчислити .

5. Властивості визначеного інтегралу.

1. Визначений інтеграл не залежить від позначення змінної

, 

оскільки результат інтегрування - число, яке не залежить від того, якою буквою позначено аргумент підінтегральної функції.

2. Визначений інтеграл від алгебраїчної суми скінченого числа неперервних функцій, заданих на відрізку  дорівнює алгебраїчній сумі визначених інтегралів:

.

3. Сталий множник  виноситься за знак визначеного інтегралу:

 

4. Якщо верхню і нижню межі інтегрування поміняти місцями, то визначений інтеграл змінить знак на протилежний при збереженні абсолютної величини

 

5. Якщо межі інтегрування рівні, то визначений інтеграл дорівнює нулю:

 

6.  при .

7. Адитивна властивість: якщо проміжок  розбити на дві частини  і , то



8. Якщо підінтегральна функція на проміжку інтегрування зберігає постійний знак, то інтеграл буде число того ж знаку, що і функція, тобто якщо  , то 

 

Слайд 12

Приклад 6. Обчислити визначений інтеграл (знайдіть помилку в розв’язку)

а) ;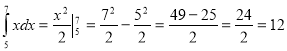

б)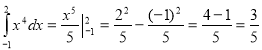

(є помилка )

в)

Слайд 13

1. Обчисліть інтеграл

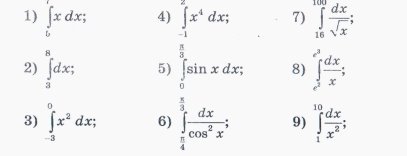
Слайд 14

2. Обчисліть площу криволінійної трапеції, зображеної на рисунку.

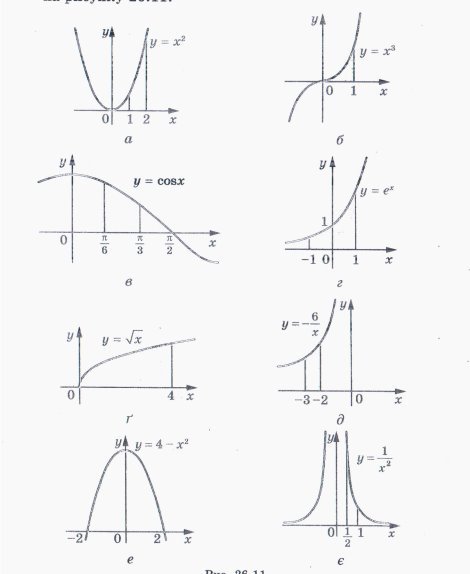
Підсумки. Закінчіть речення

- Щоб обчислити визначений інтеграл потрібно…

Рефлексія

• Що було нового?
• Чи важко було сьогодні вивчати нову тему?
• Які труднощі виникали?

"Дифференцированию можно научить лошадь. Интегририванию лошадь научить нельзя", профессор Лурье, ЛГУ советский учёный в области теоретической и прикладной механики, член Национального комитета по теоретической и прикладной механике, член-корреспондент АН СССР