Урок по алгебре и началам анализа 11 класса по теме «Применение производной к исследованию функции»
Урок по алгебре и началам анализа 11 класса
по теме «Применение производной к исследованию функции»
Тема урока: «Применение производной для исследования функций».
Тип урока: Урок формирования новых знаний.
Задачи:
- Дать представление о связи свойств функции с её производной, учить чтению и анализу графиков функций.
- Развивать умение анализировать, сопоставлять, сравнивать, формулировать выводы по результатам собственной деятельности.
Ход урока
1. Актуализация опорных знаний
Повторение определений возрастающей, убывающей функций, точек минимума и максимума, наибольшего и наименьшего значений функции:
|
|
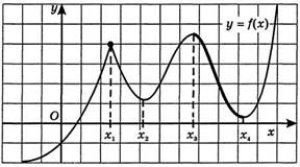
№1. По графику функции y=f(x) ответьте на вопросы:
|
|
|
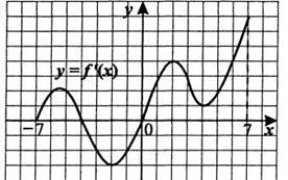
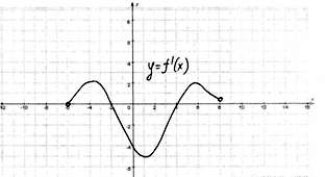
№2. По графику функции y=f ´(x) ответьте на вопросы:
|
2. Алгоритм исследования функций
- Найти производную функции y=f(x).
- Найти стационарные и критические точки.
- Отметить эти точки на числовой прямой и определить знаки производной на получившихся промежутках.
- Сделать выводы о монотонности функции и о её точках экстремума.
3. Чтобы исследовать функцию на монотонность и экстремумы, необязательно строить график производной, достаточно определить знаки производной на промежутках, на которые стационарные и критические точки разбивают область определения функции. Фактически составляется алгоритм исследования непрерывной функции на монотонность и экстремумы:
Выполнить задания такого вида:
|
|
№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции. |
|
|
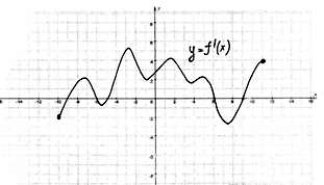
№2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её производной. Укажите количество точек графика этой функции, в которых касательная параллельна оси ОХ. |
4. Домашнее задание
|
|
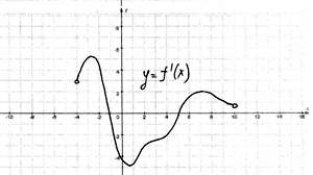
№3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график её производной. Укажите длину промежутка убывания этой функции. |
|
|
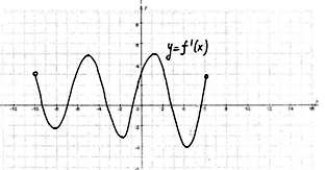
№4. Непрерывная функция y=f(x) задана на (-4;10). На рисунке изображён график её производной. Укажите число точек экстремума этой функции. |

про публікацію авторської розробки
Додати розробку