Урок "Показникові рівняння і системи та методи їх розв’язування "
Про матеріал
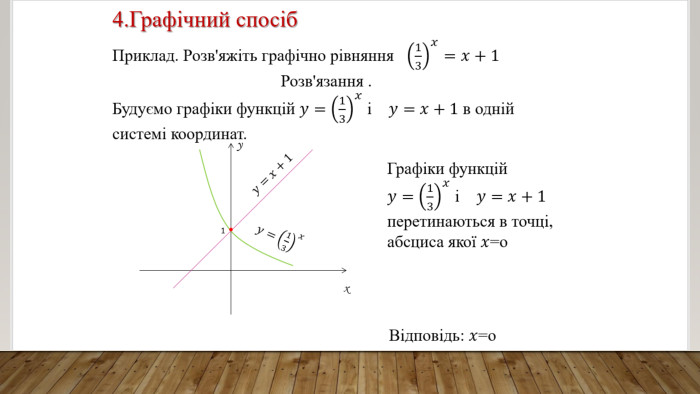
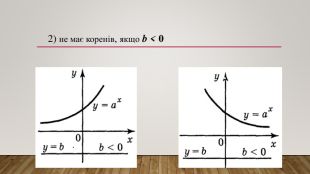
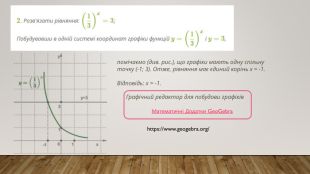
Матеріал для вивчення теми "Показникові рівняння та їх системи". Наведені методи та приклади розв'язування показникових рівнянь. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку