Урок "Показникова та логарифмічна функції. Узагальнення та систематизація.Розв'язування прикладних задач."
- в групах.docx docx
- в парах.docx docx
- видів роботи на урок.docx docx
- для груп проекти.docx docx
- Показати всі файли
|
І група: Знайдіть усі значення параметра a,при яких рівняння
|
ІІІ група: Складіть рівняння дотичної до графіка
функції f(x)=
|
|
ІІ група: Розв’яжіть нерівність:
|
ІV група: Розв’яжіть нерівність:
f ꞌ(x) ≤ g ꞌ (x) ,якщо f(x)=
|
|
І група: Знайдіть усі значення параметра a,при яких рівняння
|
ІІІ група: Складіть рівняння дотичної до графіка
функції f(x)=
|
|
ІІ група: Розв’яжіть нерівність:
|
ІV група: Розв’яжіть нерівність:
f ꞌ(x) ≤ g ꞌ (x) ,якщо f(x)=
|
|
І група: Знайдіть усі значення параметра a,при яких рівняння
|
ІІІ група: Складіть рівняння дотичної до графіка
функції f(x)=
|
|
ІІ група: Розв’яжіть нерівність:
|
ІV група: Розв’яжіть нерівність:
f ꞌ(x) ≤ g ꞌ (x) ,якщо f(x)=
|
|
І пара
а)
|
ІІ пара
а)
|
|
ІІІ пара
а)
|
ІV пара
a)
|
|
І пара
а)
|
ІІ пара
а)
|
|
ІІІ пара
а)
|
ІV пара
a)
|
|
І пара
а)
|
ІІ пара
а)
|
|
ІІІ пара
а)
|
ІV пара
a)
|
|
П. І. Учня |
|
|
1. Перевірка д/з ( 4б.)+(5б) |
|
|
2. Усні вправи (кожна правильна відповідь -1б.) |
|
|
3.Індивідуальне тестування (12 б) |
|
|
4.Робота в парах (4б) |
|
|
5. Робота в групах (4б) |
|
|
Оцінка за урок х (обчислюється за пропорцією |
|
|
6.ЗНО 2018 №33 (разом) |
|
|
П. І. Учня |
|
|
1. Перевірка д/з ( 4б.)+(5б) |
|
|
2. Усні вправи (кожна правильна відповідь -1б.) |
|
|
3.Індивідуальне тестування (12 б) |
|
|
4.Робота в парах (4б) |
|
|
5. Робота в групах (4б) |
|
|
Оцінка за урок х (обчислюється за пропорцією |
|
|
6.ЗНО 2018 №33 (разом) |
|
|
П. І. Учня |
|
|
1. Перевірка д/з ( 4б.)+(5б) |
|
|
2. Усні вправи (кожна правильна відповідь -1б.) |
|
|
3.Індивідуальне тестування (12 б) |
|
|
4.Робота в парах (4б) |
|
|
5. Робота в групах (4б) |
|
|
Оцінка за урок х (обчислюється за пропорцією |
|
|
6.ЗНО 2018 №33 (разом) |
|
*максимум набраних балів у класі
|
1)Астрономія Завдання на визначення річного паралакса зірки. Обчислити річний паралакс і відстань до Веги (α Ліри), якщо її абсолютна і видима зоряні величини відповідно рівні 0,5 і 0,1. Скористайтеся формулою М= m+5+5.lg(p ”), D= 1/p”
Цікаві відомості: Вегу легко дізнатися по блиску синьо-білого кольору, яка знаходиться в маленькому і компактному сузір’ї Ліри. Це сузір’я складається в основному з Веги і чотирьох слабких зірок у вигляді паралелограма. Вега (α Ліри) – найяскравіша зірка в сузір’ї Ліри, п’ята по яскравості зірка нічного неба і друга (після Арктура) – в Північній півкулі.
|
|
3)Економіка,Соціальна сфера Згідно з даними перепису населення України станом на 1 січня 2017 року складало 44,83 млн. осіб,а на 1 січня 2018 - 42,386 млн.осіб.Через скільки років населення країни досягне критичного значення в 1 млн. осіб,якщо ситуація в Україні не зміниться.(Відсотковий приріст вважати сталим).Скористайтеся формулою складених відсотків.
А=Аₒ(1+ Запропонуйте вирішення цієї проблеми.
Біологія Хвора на грип людина не залишилася вдома,а прийшла до школи.Якщо вважати,що кількість бактерій в той момент,коли людина прийшла до школи 7,а через 2 години сприятливих умов їх кількість зросла до 100,то через який момент часу їх стане 1000? Скількох людей встигне заразити хворий,якщо вважати,що він виходив із класу,кашляв,чхав і бактерії постійно потрапляли у сприятливе середовище,якщо для того щоб людина захворіла достатньо 10 бактерій.
Пам’ятка «Не хворій!» «Цього року очікують три нові штами грипу. Йдеться не про пандемічний, до якого ми звикли, H1N1 Каліфорнія. Замість нього прийдуть одразу три нові штами: H1N1 H3N2 Сингапур, H1N1 Мічиган та B Колорадо, який виявили у США торік». Як приготувати організм, щоб не захворіти на грип? Визначають три основні складові, які допомагають організму протистояти вірусу грипу – харчування, загартовування та сезонна вакцинація. Раціональне харчування та водний баланс. Збалансоване харчування забезпечує організм усіма необхідними мікро-, макроелементами та вітамінами. До цього обов’язково додається достатнє насичення організму водою. Медики називають це «оптимальним режимом наводнення організму». Він корисний тим, що допомагає організму не тільки доставити необхідні елементи, але й промити організм, виводячи з нього, в тому числі, все, що може сприяти розвитку захворюванням. Загартовування. «Воно добре спрацьовує саме в такий період, як зараз. Фактично загартовуванням ми готуємо організм до осінніх та весняних перепадів температури. Тренована загартовуванням людина набагато стійкіше реагує на різкі сезонні зміни температури і, відповідно, її імунітет набагато ефективніше бореться з вірусами. Вакцинація. На сьогодні це доведений ефективний спосіб протистояти грипу. В звичайних умовах вакциновані від грипу ним не хворіють. У випадках епідемії, коли вірусу довкола надто багато, вакциновані в окремих випадках можуть отримати хіба легку форму хвороби з незначними ознаками ГРВІ і без ускладнень, можливих після важкої форми грипу. «Вакциновані від грипу не мають ускладнень, навіть якщо й хворіють. Але знову ж таки, вакцина є лише від грипу, на жаль, немає від парагрипу чи ентеровірусної інфекції»
|
|
Інформатика Який об’єм інформації несе наступне повідомлення,якщо його закодовано буквами українського алфавіту(знаками пунктуації знехтувати).Скористайтеся формулою Хартлі i=log2N, де i – кількість інформації у бітах), N – кількість інформаційних повідомлень.
Кібербулінг Це використання телефона, комп’ютера та інших ґаджетів для цькування, яке розгортається у віртуальному світі, в кіберпросторі, зокрема в соціальних мережах. Часто людина, яку цькують у реальному житті, зазнає нападок і в кіберпросторі. На відміну від шкільного булінгу, який закінчується за межами школи, кібербулінг не закінчується ніде. Що більше наше життя переходить в онлайн, то більш безперервним стає кібербулінг. Інколи цькування в кіберпросторі стає таким нестерпним, що знижує не лише самооцінку й настрій, але й шкодить здоров’ю через безсоння, постійні переживання. Булінг часом ламає життя: змушує міняти школу, навіть місто. У випадку важких трагічних наслідків зазвичай для тих, хто брав участь у цькуванні, це стає шоком: жартували-жартували — і раптом… Це відбувається тому, що цькувальникам дуже важко уявити себе на місці зацькованого і зрозуміти глибину його переживань. Для одних це смішна сцена, а для іншого — важка травма. Зосереджуючись на зовнішньому вигляді сцени, яка розгортається (як на екрані), цькувальники вважають, що у звичних жартах немає нічого разючого, болючого чи насильницького, а якщо було би, то жертва сказала би, звернулася по допомогу. Але часто виявляється, що мішень цькування почувається жертвою, якій ніхто не хоче й не може допомогти. Це дуже важкі переживання, часто настільки важкі, що жертва психологічно ламається, починає мститися й сама стає цькувальником, виміщає свої образи на слабшому. Утворюється автоматичний ланцюжок передачі насильства: цькувальники не можуть зупинитися, а жертва не може перервати цієї ситуації. Як же припинити цькування? Найменше зусиль для подолання булінгу потребує спостерігач. Але часто спостерігачі відсторонюються: їм і не подобається ця ситуація (не смішно), й не хочеться втручатися, бо, гляди, почнуть і з тебе насміхатися. Та саме через таке невтручання все й відбувається. Невтручання підтримує насильника. Буває достатньо одному спостерігачу набратися сміливості і сказати «досить», як ситуація змінюється. Жертва вже не почувається жертвою — самотньою й нікому не потрібною. А цькувальники починають розуміти, що нападки — це не смішно, а «тренувати гумор» можна в інший спосіб. У кіберпросторі спрацьовують такі ж психологічні механізми. Не будьте байдужими спостерігачами. Це може врятувати комусь життя. Не ставайте автоматично в коло цькувальників. Приєднуючись до маси нападників, ви втрачаєте себе. Психологи давно знають: у натовпі людина може зробити таке, чого при здоровому глузді ніколи не зробила би з власної ініціативи. Не дуже приємна перспектива стати щупальцями безмозкого монстра-цькувальника, замість почуватися людиною, яка має самоповагу й пишається власними гідними та сміливими вчинками. В інтернеті ви можете знайти сайти програм «Стоп-цькування» з мультфільмами й короткими фільмами, зокрема сайт www.stopbullying.gov.
|
Математика 11 клас
(1-й урок пари)
Тема: Підсумковий урок з теми «Показникова та логарифмічна функції»
Мета: Повторити, узагальнити, систематизувати вивчений матеріал про показникову та логарифмічну функції, показати вміння розв'язувати показникові та логарифмічні рівняння та нерівності. Виховувати увагу, логічне мислення, самостійність, культуру математичної мови та записів.
Тип уроку: узагальнення та систематизації знань та вмінь.
Епіграф до уроку: Математика - наука молодих. Інакше й не може бути. Заняття математикою – це така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості. Н. Вінер
Хід уроку
I. Організаційний момент:
1.Привітання
Сьогодні ми на уроці
Уважні
Серьйозні
Привітні
Інтегровані
Швидкі
Неординарні
Інформовані
ІІ.Формулювання теми,мети і завдань уроку
Кожний учень отримав перелік всіх видів роботи на уроці:
|
П. І. Учня |
|
|
1. Перевірка д/з ( 4б.)+(5б) |
|
|
2. Усні вправи (кожна правильна відповідь -1б.) |
|
|
3.Індивідуальне тестування (12 б) |
|
|
4.Робота в парах (4б) |
|
|
5. Робота в групах (4б) |
|
|
Оцінка за урок х (обчислюється за пропорцією |
|
|
6.ЗНО 2018 №33 (разом) |
|
ІІІ Узагальнення та систематизація знань
Перевірка домашнього завдання
1.Перевірка домашнього завдання
(4б)Домашнє завдання було груповим.Вам пропонувалося поділитися на 2 групи,одна з яких «Показникова функція»,а інша – «Логарифмічна функція», та оформити сторінку у Facebook. А поки там налаштовуються,ми перувіримо домашні приклади.
(5б)Розв![]() язок домашньої роботи:
язок домашньої роботи:
1) ![]() (1;
(1; ![]()
2) ![]() +
+![]() =20; х=1
=20; х=1
3) ![]() ; х=16
; х=16
4)![]() (
(![]()
5) Складіть рівняння дотичної до графіка функції f(x)=![]() у точці з абсцисою хₒ= -1 ; у=4х+4
у точці з абсцисою хₒ= -1 ; у=4х+4
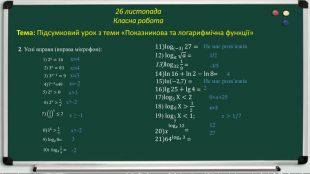
(1завдання-1 б) 2. Усні вправи (вправа мікрофон):
1) ![]() х=4
х=4 ![]()
![]()
2) ![]() х=4 12)
х=4 12)![]() =
= ![]()
3) ![]() х=3 13)
х=3 13) ![]() = -
= - ![]()
![]() =49 х=-2
=49 х=-2 ![]() =4
=4
5) ![]() х>3
х>3 ![]()
6) ![]() ; х
; х ![]() -2
-2 ![]() =2
=2
![]() х≥-1 17)
х≥-1 17)![]() 0<х<25
0<х<25
![]()
![]() х>-2 18)
х>-2 18) ![]() х>3
х>3
9) ![]() = 3 19)
= 3 19) ![]() х>
х>![]()
10) ![]() -2
-2 ![]() =12
=12
![]() = 27
= 27
(12б) 3.Індивідуальна робота:
Тестування:
№1 Яка з даних функцій не є показниковою
А) y=(![]() ; Б) у=
; Б) у=![]() ; В) у=
; В) у= ![]() ; Г) у=
; Г) у=![]()
№2 У якій точці перетинаються графіки функцій у=![]() і у=
і у= ![]()
А) (1;1) Б) (1; 0) В) (0;1) Г) (0; -1)
№3 Зростаючою чи спадною є функція у=![]()
А) Зростаючою Б) Ні зростаючою, ні спадною; В) Спадною Г) Інша відповідь
№4Обчисліть ![]()
А) 2; Б) 7; В) -2; Г) ![]() ;
;
№5Обчисліть ![]()
А) 6; Б) 3; В) 8; Г) 2;
№6 Розв'яжіть нерівність ![]()
А) (0; 4) Б) (0; 4] В) х![]()
№7 Розв'яжіть рівняння lgx = 1 – lg2
А)5 Б)-5 В)1 Г)2
№8 Розв'яжіть рівняння ![]()
А) 25 Б) 2 В) 30 Г) 10
№9 Розв'яжіть нерівність ![]()
А) х![]() Б) х
Б) х![]() В) х
В) х![]()
№10 Розв'яжіть нерівність ![]()
А) х![]()
№11Розв'яжіть нерівність ![]()
А)х>1 Б) х≤ ![]() В) х≤ 4 Г) х≥ 8
В) х≤ 4 Г) х≥ 8
№12 Розв'яжіть рівняння ![]() = 9
= 9
А) -2 Б) 2 В) 1 Г) -1
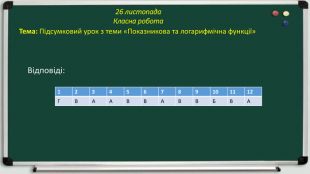
|
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
№7 |
№8 |
№9 |
№10 |
№11 |
№12 |
|
Г |
В |
А |
А |
В |
В |
А |
В |
В |
Б |
В |
А |
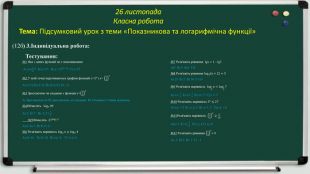
4.Робота в парах: Розв’яжіть рівняння та нерівності:
І пара: ІІ пара
а)![]() +
+![]() =0 а)
=0 а)![]() - 36∙
- 36∙![]() 0
0
В: х=6 В: x=1;x=2
ІІІ пара: ІV пара:
а)![]() +
+![]() <2 a)
<2 a)![]() +4∙
+4∙![]() ≥ 539
≥ 539
В: хє(2;7) U (22;27)
В: хє(1;+∞)
5.Робота в групах:
І група: ІІІ група:
Знайдіть усі значення параметра Складіть рівняння дотичної до графіка
a,при яких рівняння функції f(x)=![]() у точці з абсцисою
у точці з абсцисою
![]() +
+![]() -а=0 не має коренів. хₒ=-1
-а=0 не має коренів. хₒ=-1
В:а є (-1;0] В: у=2х+2
ІІ група: ІV група:
Розв’яжіть нерівність: Розв’яжіть нерівність:
f ꞌ(x) ≤ g ꞌ (x) ,якщо f(x)=![]() (
(![]() -3x+1),
-3x+1),
![]()
![]() В: хє[1;1000] g(x)=2x
В: хє[1;1000] g(x)=2x![]() В:хє[-1;4]
В:хє[-1;4]
ІV. Підсумок (обчислення балів)
6.ЗНО 2018 Додатково (на ДІЗ)
№ 33 . Розв’яжіть нерівність ![]() 0 залежно від значень параметра .
0 залежно від значень параметра .
V. Домашнє завдання Параграф 13-20 підручника,сторінки у FB
Опрацювати завдання всіх груп і пар.
Математика 11 клас
(2-й урок пари)
Тема:Застосування логарифмічної та показникової функцій до розв’язування
прикладних задач.
Мета уроку: узагальнити та систематизувати навички учнів з теми «Показникові та логарифмічні функції», розширити уявлення учнів про застосування показникової та логарифмічної функцій в різних сферах діяльності людини;розвивати увагу, грамотну математичну мову, уміння працювати в команді,активізувати пізнавальну діяльність;виховувати працьовитість, активність,інтерес до математики.
Форма проведення: урок-проект.
Епіграф до уроку: « Яка наука може бути більш благородною, більш чудовою, більш корисною для людства, ніж математика»
Б.Франклін
Хід уроку
І Організаційний момент.
ІІ Мотивація(перегляд презентації «Логарифмічна спіраль»)
Протягом 16 століття швидко зростала кількість наближених обчислень,особливо в астрономії. Вдосконалення інструментів дослідження руху планет та інші роботи потребували колосальних,іноді багаторічних,розрахунків.Астрономам загрожувала реальна небезпека потонути в невиконаних розрахунках.
Тоді математики для спрощення обчислень придумали логарифми.І три століття з того дня,як в 1614 році було надруковано перші логарифмічні таблиці,складені шотландським математиком Джоном Непером,вони вірою і правдою слугували астрономам і геодезистам,інженерам і морякам,скорочуючи час на обчислення та тим самим подовжуючи життя тим,хто займався цими обчисленнями.
Тому і сьогодні я хочу поставити питання : «Для чого нам потрібні логарифми?
Логарифми-це примха математиків чи життєва необхідність?»(слайд-діаграма опитування батьків)
Перед вивченням теми ми разом з вами провели соціальне опитування серед батьків вашого класу.Вони відповідали на 2 питання:
1)Чи знаєте ви ,що таке логарифм числа,показникова та логарифмічна функції?
2)Якщо на перше питання відповіли так,то чи знаєте ви практичне застосування логарифмам?
Всього 3 з 36 опитаних ствердно відповіли на 1-е питання,але не змогли дати відповідь на 2-е питання.Тому я дуже сподіваюся,що коли вас будуть запитувати ви ствердно відповісте на обидва питання.
ІІІ Постановка задачі
Отже я хочу ще раз поставити питання:
«Для чого нам потрібні логарифми?
Логарифми-це примха математиків чи життєва необхідність?»
А в кінці уроку ви дасте відповідь на нього.
Задача кожної групи:1)Вирішити поставлену задачу
2)Дати відповідь на вище поставлене питання
Оформлення довільне
Розподіл класу на 4 групи:
1)Астрономія
Завдання на визначення річного паралакса зірки.
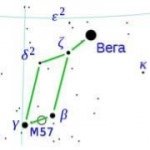
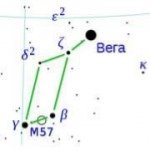
Обчислити річний паралакс і відстань до Веги (α Ліри), якщо її абсолютна і видима зоряні величини відповідно рівні 0,5 і 0,1. Скористайтеся формулою М= m+5+5.lg(p ”), D= 1/p”
Цікаві відомості:
Вегу легко дізнатися по блиску синьо-білого кольору, яка знаходиться в маленькому і компактному сузір’ї Ліри. Це сузір’я складається в основному з Веги і чотирьох слабких зірок у вигляді паралелограма. Вега (α Ліри) – найяскравіша зірка в сузір’ї Ліри, п’ята по яскравості зірка нічного неба і друга (після Арктура) – в Північній півкулі.
Розв’язання:
М= m+5+5.lg(p ”)
lg(p ”)=(М-m-5)/5
lg(p ”)=(0,5-0,1-5)/5
lg(p ”)=-0,92
p ” = 10-0.92 = 0,12”
D= 1/p”
D= 1/0,12” = 8,3 пк
Задача
2)Біологія
Хвора на грип людина не залишилася вдома,а прийшла до школи.Якщо вважати,що кількість бактерій в той момент,коли людина прийшла до школи 7,а через 2 години сприятливих умов їх кількість зросла до 100,то через який момент часу їх стане 1000? Скількох людей встигне заразити хворий,якщо вважати,що він виходив із класу,кашляв,чхав і бактерії постійно потрапляли у сприятливе середовище,якщо для того щоб людина захворіла достатньо 10 бактерій.
Пам’ятка «Не хворій!»
«Цього року очікують три нові штами грипу. Йдеться не про пандемічний, до якого ми звикли, H1N1 Каліфорнія. Замість нього прийдуть одразу три нові штами: H1N1 H3N2 Сингапур, H1N1 Мічиган та B Колорадо, який виявили у США торік».
Як приготувати організм, щоб не захворіти на грип?
Визначають три основні складові, які допомагають організму протистояти вірусу грипу – харчування, загартовування та сезонна вакцинація.
Раціональне харчування та водний баланс. Збалансоване харчування забезпечує організм усіма необхідними мікро-, макроелементами та вітамінами. До цього обов’язково додається достатнє насичення організму водою. Медики називають це «оптимальним режимом наводнення організму». Він корисний тим, що допомагає організму не тільки доставити необхідні елементи, але й промити організм, виводячи з нього, в тому числі, все, що може сприяти розвитку захворюванням.
Загартовування. «Воно добре спрацьовує саме в такий період, як зараз. Фактично загартовуванням ми готуємо організм до осінніх та весняних перепадів температури. Тренована загартовуванням людина набагато стійкіше реагує на різкі сезонні зміни температури і, відповідно, її імунітет набагато ефективніше бореться з вірусами.
Вакцинація. На сьогодні це доведений ефективний спосіб протистояти грипу. В звичайних умовах вакциновані від грипу ним не хворіють. У випадках епідемії, коли вірусу довкола надто багато, вакциновані в окремих випадках можуть отримати хіба легку форму хвороби з незначними ознаками ГРВІ і без ускладнень, можливих після важкої форми грипу.
«Вакциновані від грипу не мають ускладнень, навіть якщо й хворіють. Але знову ж таки, вакцина є лише від грипу, на жаль, немає від парагрипу чи ентеровірусної інфекції»
Рішення:
(![]() -
-![]() ):2=(
):2=(![]() -
-![]() ):t
):t
t= ![]() =
= ![]() = 2
= 2![]() =2∙1,864=3,728=3год 43хв
=2∙1,864=3,728=3год 43хв
n=1000:10-10=90(учнів)
3)Економіка,Соціальна сфера
Згідно з даними перепису населення України станом на 1 січня 2017 року складало 44,83 млн. осіб,а на 1 січня 2018 - 42,386 млн.осіб.Через скільки років населення країни досягне критичного значення в 1 млн. осіб,якщо ситуація в Україні не зміниться.(Відсотковий приріст вважати сталим).Скористайтеся формулою складених відсотків.
А=Аₒ(1+![]() )ⁿ
)ⁿ
Рішення:
1)р=![]() ∙100%=
∙100%=![]() 100%=-5,45%
100%=-5,45%
2)(1-0,0545)ⁿ =![]()
n=![]() =67 (років)
=67 (років)
4) Інформатика
Який об’єм інформації несе наступне повідомлення,якщо його закодовано буквами українського алфавіту(знаками пунктуації знехтувати).Скористайтеся формулою Хартлі i=log2N, де i – кількість інформації у бітах), N – кількість інформаційних повідомлень.
Кібербулінг
Це використання телефона, комп’ютера та інших ґаджетів для цькування, яке розгортається у віртуальному світі, в кіберпросторі, зокрема в соціальних мережах.
Часто людина, яку цькують у реальному житті, зазнає нападок і в кіберпросторі. На відміну від шкільного булінгу, який закінчується за межами школи, кібербулінг не закінчується ніде. Що більше наше життя переходить в онлайн, то більш безперервним стає кібербулінг.
Інколи цькування в кіберпросторі стає таким нестерпним, що знижує не лише самооцінку й настрій, але й шкодить здоров’ю через безсоння, постійні переживання. Булінг часом ламає життя: змушує міняти школу, навіть місто.
У випадку важких трагічних наслідків зазвичай для тих, хто брав участь у цькуванні, це стає шоком: жартували-жартували — і раптом… Це відбувається тому, що цькувальникам дуже важко уявити себе на місці зацькованого і зрозуміти глибину його переживань. Для одних це смішна сцена, а для іншого — важка травма.
Зосереджуючись на зовнішньому вигляді сцени, яка розгортається (як на екрані), цькувальники вважають, що у звичних жартах немає нічого разючого, болючого чи насильницького, а якщо було би, то жертва сказала би, звернулася по допомогу. Але часто виявляється, що мішень цькування почувається жертвою, якій ніхто не хоче й не може допомогти. Це дуже важкі переживання, часто настільки важкі, що жертва психологічно ламається, починає мститися й сама стає цькувальником, виміщає свої образи на слабшому. Утворюється автоматичний ланцюжок передачі насильства: цькувальники не можуть зупинитися, а жертва не може перервати цієї ситуації.
Як же припинити цькування? Найменше зусиль для подолання булінгу потребує спостерігач. Але часто спостерігачі відсторонюються: їм і не подобається ця ситуація (не смішно), й не хочеться втручатися, бо, гляди, почнуть і з тебе насміхатися. Та саме через таке невтручання все й відбувається. Невтручання підтримує насильника. Буває достатньо одному спостерігачу набратися сміливості і сказати «досить», як ситуація змінюється. Жертва вже не почувається жертвою — самотньою й нікому не потрібною. А цькувальники починають розуміти, що нападки — це не смішно, а «тренувати гумор» можна в інший спосіб.
У кіберпросторі спрацьовують такі ж психологічні механізми. Не будьте байдужими спостерігачами. Це може врятувати комусь життя. Не ставайте автоматично в коло цькувальників. Приєднуючись до маси нападників, ви втрачаєте себе. Психологи давно знають: у натовпі людина може зробити таке, чого при здоровому глузді ніколи не зробила би з власної ініціативи. Не дуже приємна перспектива стати щупальцями безмозкого монстра-цькувальника, замість почуватися людиною, яка має самоповагу й пишається власними гідними та сміливими вчинками.
В інтернеті ви можете знайти сайти програм «Стоп-цькування» з мультфільмами й короткими фільмами, зокрема сайт www.stopbullying.gov.
Рішення: букв у рядку-66
Рядків-38
i=66∙38∙ ![]() =12540 біт=12,25кбайт
=12540 біт=12,25кбайт
Кожна група отримує певну задачу ,яку потрібно вирішати і готує презентацію.
ІV. Захист міні-проектів.
V.Підсумок уроку.(УСПІШНІ) Скільки букв у слові?Ащо означає число 7?
|
Тестування: №1 Яка з даних функцій не є показниковою
А) y=(
№2 У якій точці перетинаються графіки функцій у= А) (1;1) Б) (1; 0) В) (0;1) Г) (0; -1)
№3 Зростаючою чи спадною є функція у= А) Зростаючою Б) Ні зростаючою, ні спадною; В) Спадною Г) Інша відповідь
№4Обчисліть
А) 2; Б) 7; В) -2; Г)
№5Обчисліть А) 6; Б) 3; В) 8; Г) 2;
№6 Розв'яжіть нерівність
А) (0; 4) Б) (0; 4] В) х №7 Розв'яжіть рівняння lgx = 1 – lg2 А)5 Б)-5 В)1 Г)2
№8 Розв'яжіть рівняння А) 25 Б) 2 В) 30 Г) 10
№9 Розв'яжіть нерівність
А) х
№10 Розв'яжіть нерівність
А) х
№11Розв'яжіть нерівність
А)х>1 Б) х≤
№12 Розв'яжіть рівняння А) -2 Б) 2 В) 1 Г) -1
|
Тестування: №1 Яка з даних функцій не є показниковою
А) y=(
№2 У якій точці перетинаються графіки функцій у= А) (1;1) Б) (1; 0) В) (0;1) Г) (0; -1)
№3 Зростаючою чи спадною є функція у= А) Зростаючою Б) Ні зростаючою, ні спадною; В) Спадною Г) Інша відповідь
№4Обчисліть
А) 2; Б) 7; В) -2; Г)
№5Обчисліть А) 6; Б) 3; В) 8; Г) 2;
№6 Розв'яжіть нерівність
А) (0; 4) Б) (0; 4] В) х №7 Розв'яжіть рівняння lgx = 1 – lg2 А)5 Б)-5 В)1 Г)2
№8 Розв'яжіть рівняння А) 25 Б) 2 В) 30 Г) 10
№9 Розв'яжіть нерівність
А) х
№10 Розв'яжіть нерівність
А) х
№11Розв'яжіть нерівність
А)х>1 Б) х≤
№12 Розв'яжіть рівняння А) -2 Б) 2 В) 1 Г) -1
|


про публікацію авторської розробки
Додати розробку





![26 листопада. Класна робота. Тема: Підсумковий урок з теми «Показникова та логарифмічна функції»№7 Розв'яжіть рівняння lgx = 1 – lg2 А)5 Б)-5 В)1 Г)2№8 Розв'яжіть рівняння log2х+2=5 А) 25 Б) 2 В) 30 Г) 10№9 Розв'яжіть нерівність log15х<log157 А) х<17 Б) х>17 В) х>7 Г) х<7№10 Розв'яжіть нерівність 3х≤27 А) х≤−3 Б) х≤3 В) х<3 Г)х≥−3№11 Розв'яжіть нерівність 12х≥116 А)х>1 Б) х≤ 18 В) х≤ 4 Г) х≥ 8№12 Розв'яжіть рівняння 13х= 9 А) -2 Б) 2 В) 1 Г) -1 (12б) 3.Індивідуальна робота: Тестування:№1 Яка з даних функцій не є показниковою А) y=(12)𝑥; Б) у=𝜋х; В) у= 2х3−х; Г) у=х𝜋№2 У якій точці перетинаються графіки функцій у=2х і у= 18х. А) (1;1) Б) (1; 0) В) (0;1) Г) (0; -1)№3 Зростаючою чи спадною є функція у=32х. А) Зростаючою Б) Ні зростаючою, ні спадною; В) Спадною Г) Інша відповідь№4 Обчисліть log749 А) 2; Б) 7; В) -2; Г) 12; №5 Обчисліть 27log32 А) 6; Б) 3; В) 8; Г) 2;№6 Розв'яжіть нерівність log3х≤log34 А) (0; 4) Б) (0; 4] В) х≤4; Г) х≥4 26 листопада. Класна робота. Тема: Підсумковий урок з теми «Показникова та логарифмічна функції»№7 Розв'яжіть рівняння lgx = 1 – lg2 А)5 Б)-5 В)1 Г)2№8 Розв'яжіть рівняння log2х+2=5 А) 25 Б) 2 В) 30 Г) 10№9 Розв'яжіть нерівність log15х<log157 А) х<17 Б) х>17 В) х>7 Г) х<7№10 Розв'яжіть нерівність 3х≤27 А) х≤−3 Б) х≤3 В) х<3 Г)х≥−3№11 Розв'яжіть нерівність 12х≥116 А)х>1 Б) х≤ 18 В) х≤ 4 Г) х≥ 8№12 Розв'яжіть рівняння 13х= 9 А) -2 Б) 2 В) 1 Г) -1 (12б) 3.Індивідуальна робота: Тестування:№1 Яка з даних функцій не є показниковою А) y=(12)𝑥; Б) у=𝜋х; В) у= 2х3−х; Г) у=х𝜋№2 У якій точці перетинаються графіки функцій у=2х і у= 18х. А) (1;1) Б) (1; 0) В) (0;1) Г) (0; -1)№3 Зростаючою чи спадною є функція у=32х. А) Зростаючою Б) Ні зростаючою, ні спадною; В) Спадною Г) Інша відповідь№4 Обчисліть log749 А) 2; Б) 7; В) -2; Г) 12; №5 Обчисліть 27log32 А) 6; Б) 3; В) 8; Г) 2;№6 Розв'яжіть нерівність log3х≤log34 А) (0; 4) Б) (0; 4] В) х≤4; Г) х≥4](/uploads/files/257305/87436/93240_images/5.jpg)


![26 листопада. Класна робота. Тема: Підсумковий урок з теми «Показникова та логарифмічна функції» 4. Робота в групах:І група: ІІІ група: Знайдіть усі значення параметра Складіть рівняння дотичної до графіка a,при яких рівняння функції f(x)=ln(2𝑥+3) у точці з абсцисою 4х +а∙2х+1-а=0 не має коренів. хₒ=-1 ІІ група: ІV група: Розв’яжіть нерівність: Розв’яжіть нерівність: f ꞌ(x) ≤ g ꞌ (x) ,якщо f(x)=𝑒𝑥(𝑥2-3x+1),(х10 )lgх−2 ≤100 g(x)=2x𝑒𝑥 В:а є (-1;0] В: у=2х+2 В: хє[1;1000] В:хє[-1;4] 26 листопада. Класна робота. Тема: Підсумковий урок з теми «Показникова та логарифмічна функції» 4. Робота в групах:І група: ІІІ група: Знайдіть усі значення параметра Складіть рівняння дотичної до графіка a,при яких рівняння функції f(x)=ln(2𝑥+3) у точці з абсцисою 4х +а∙2х+1-а=0 не має коренів. хₒ=-1 ІІ група: ІV група: Розв’яжіть нерівність: Розв’яжіть нерівність: f ꞌ(x) ≤ g ꞌ (x) ,якщо f(x)=𝑒𝑥(𝑥2-3x+1),(х10 )lgх−2 ≤100 g(x)=2x𝑒𝑥 В:а є (-1;0] В: у=2х+2 В: хє[1;1000] В:хє[-1;4]](/uploads/files/257305/87436/93240_images/8.jpg)