Розробка уроку "Повторення. Похідна функції, її геометричний і механічний зміст"
Запропонована розробка уроку розрахована на дві академічні години в 11 класі.
Урок 1, 2
Тема: Повторення. Похідна функції, її геометричний і механічний зміст.
Мета:
1) Систематизувати і поглибити теоретичні та практичні знання учнів.
2) Формувати вміння працювати з джерелами додаткової інформації, аналізувати її.
3) Розвивати логічне мислення, культуру математичного мовлення, інтерес до предмету.
4) Виховувати уважність, активність, самостійність учнів, наполегливість у досягненні мети.
Хід уроку:
І. Перевірка домашнього завдання.
ІІ. Актуалізація опорних знань.
Таблиця похідних елементарних функцій:
|
|
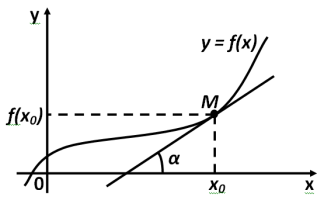
Геометричний зміст похідної:
|
Значення похідної функції y = f(x) у точці х0 дорівнює кутовому коефіцієнту дотичної до графіка функції в цій точці: f’(х0) = tg α |
|
Рівняння дотичної:
y = f’(х0) (x-х0) + f(х0)
Фізичний зміст похідної:
Похідна характеризує швидкість зміни функції при зміні аргументу. Наприклад, миттєва швидкість V нерівномірного руху є похідна від функції, яка виражає залежність пройденого шляху S від часу t.
S = S (t), V = S’ (t), a = V’ (t)
III. Усний рахунок.
Знайти похідну:
- 3х2
-
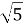 х
х
- х-5
- – 2х-10
-
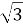 sin x
sin x
- sin2 x
-
cos

- (3 – x)5
-
8
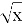
-

-
IV. Розв’язування вправ.
1. Знайти похідну:
1) y = (x3 – 2) (x2 + 1)
2) y = (![]() + 1) ( 3 – 2
+ 1) ( 3 – 2 ![]() )
)
3) y = ![]()
4) y = ![]()
5) y = (6 x5 – 2) 5
6) y = ![]()
7) y = ![]()
8) y = cos 6x
9) y = ctg (3x + ![]() )
)
10) y = sin ![]()
11) y = tg x2
12) y = cos4 3x
13) y = e6x
14) y = 62x-5
2. Розв’язати завдання зовнішнього незалежного оцінювання:
1) ЗНО 2017, завдання 20 (основна сесія):
Укажіть похідну функції y = sin x – cos x + 1.
А) y’ = cos x + sin x + 1
Б) y’ = cos x – sin x
В) y’ = – cos x – sin x + x
Г) y’ = – cos x – sin x
Д) y’ = cos x + sin x
2) ЗНО 2017, завдання 31 (додаткова сесія):
Задано функцію f (x) = x2 + 3x – 10.
1. Знайдіть похідну функції f.
2. Визначте кутовий коефіцієнт дотичної, проведеної до графіка функції f у точці з абсцисою x0 = – 1.
3) ЗНО 2016, завдання 27 (основна сесія):
Обчисліть значення похідної функції y = ![]() у точці x0 = 3.
у точці x0 = 3.
4) ЗНО 2018, завдання 31 (пробний тест):
Задано функцію f (x) = x2 – 3x – 4.
1. Знайдіть значення х = х0 , за якого похідна функції f дорівнює 1.
2. Запишіть рівняння дотичної, проведеної до графіка функції f у точці з абсцисою х0 .
5) ЗНО 2019, завдання 31 (пробний тест):
Задано функцію f (x) = ![]() + 2
+ 2
Запишіть рівняння дотичної, проведеної до графіка функції f у точці з абсцисою х0 .
6) ЗНО 2019, завдання 31 (основна сесія):
Задано функції f (x) = ![]() і g (x) = 5 – 8x
і g (x) = 5 – 8x
1. Знайдіть похідну функції f.
2. До графіка функції f проведено дотичні, паралельні графіку функції g. Визначте абсциси точок дотику.
3. Розв’язати завдання із збірника для підготовки до ЗНО:
24.5. Знайти похідну функції y = ln(2x) + 2x3 – 3.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
24.10. Знайти кут, який утворює з додатним напрямом осі Ох дотична до графіка функції y = ![]() x4 y точці x0 = – 1.
x4 y точці x0 = – 1.
|
А |
Б |
В |
Г |
Д |
|
30° |
45° |
120° |
135° |
150° |
24.16. Тіло рухається за законом s(t) = t2 – 4![]() . Знайти швидкість тіла в момент t0 = 4.
. Знайти швидкість тіла в момент t0 = 4.
|
А |
Б |
В |
Г |
Д |
|
5 |
4,75 |
12 |
7 |
7,875 |
24.19. Обчислити f’(x), якщо f(x) = sin2(2x + 0,5).
|
А |
Б |
В |
Г |
Д |
|
2(2x + 0,5)cos2x × × (2x + 0,5) |
2cos(4x + 1) |
–2cos(4x + 1) |
2sin(4x + 1) |
–2sin(4x + 1) |
24.20. Обчислити значення похідної функції y =(3x+1)3 cos3(x2 +2x+1)+![]() у точці x0 = – 1.
у точці x0 = – 1.
|
А |
Б |
В |
Г |
Д |
|
36 |
12 |
– 12 |
0 |
36 + |
24.21. Матеріальна точка рухається прямолінійно за законом
s(t) = 2,5t2 –15t , S – шлях у метрах, t – час у секундах. Через який час від початку руху ця точка зупинилася?
|
А |
Б |
В |
Г |
Д |
|
1 с |
2 с |
3 с |
3,5 с |
4 с |
24.23. Дано фунцію y = │3x + 2│. У якій точці немає похідної?
|
А |
Б |
В |
Г |
Д |
|
2 |
– 2 |
– |
– |
Похідна існує в будь-якій точці х0 ϵ R |
24.24. Обчислити похідну функції y = │2x – 5│ на проміжку (–∞; 0 ]
|
А |
Б |
В |
Г |
Д |
|
2,5 |
5 |
– 5 |
2 |
– 2 |
V. Підсумок уроку.
VI. Завдання додому.


про публікацію авторської розробки
Додати розробку