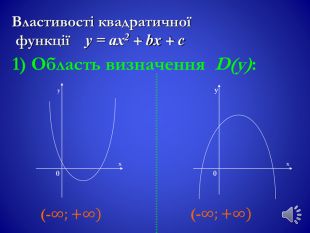
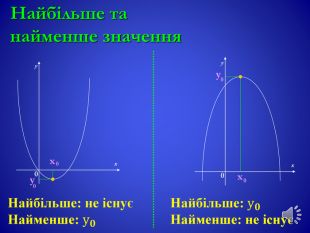
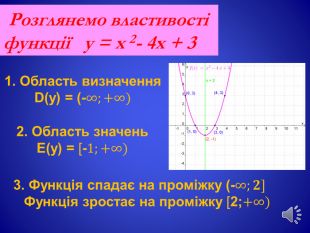
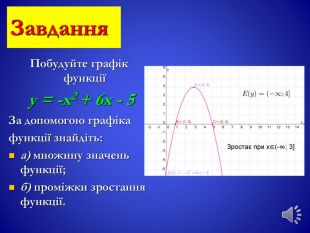
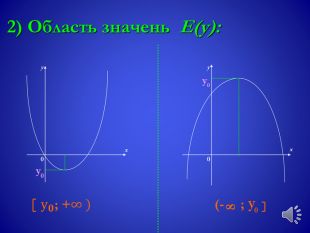Урок, Презентація, " Квадратична функція"
Про матеріал
Ввести означення квадратичної функції, формувати в учнів уміння будувати її графік; ознайомити із формулами для обчислення координат вершини параболи, навчити знаходити точки перетину з осями координат. Сформувати властивості квадратичної функції. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



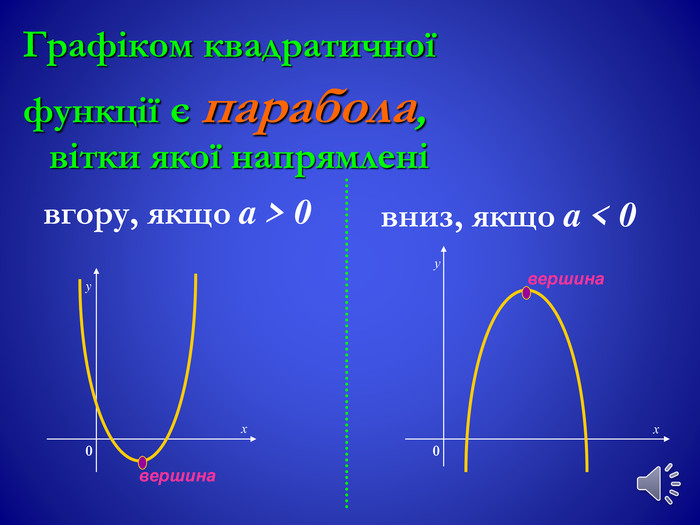




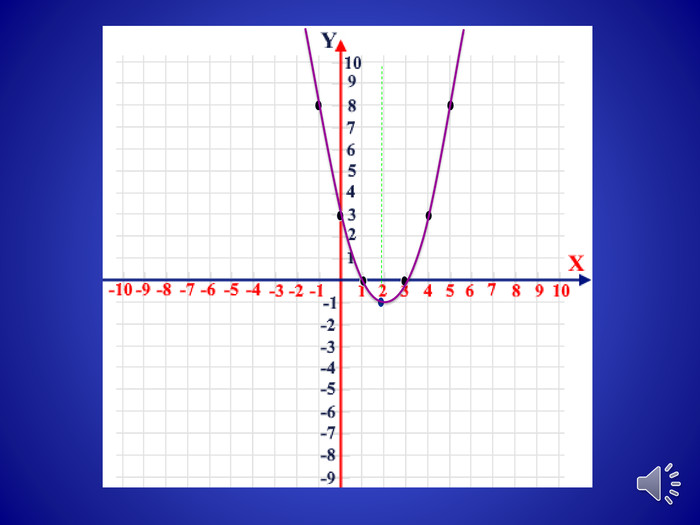


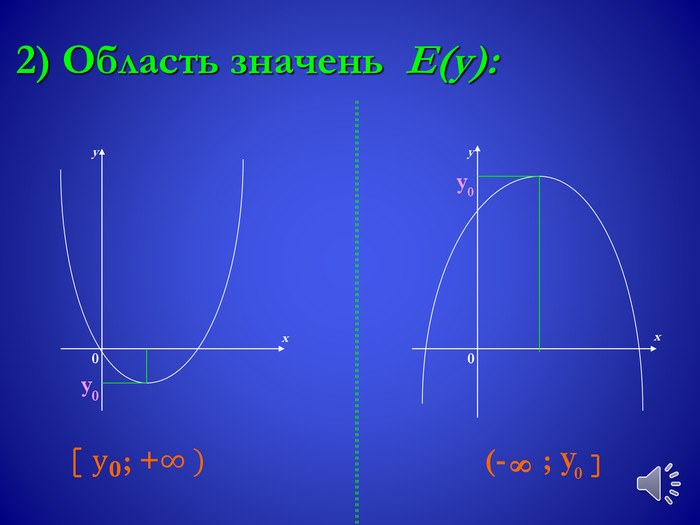
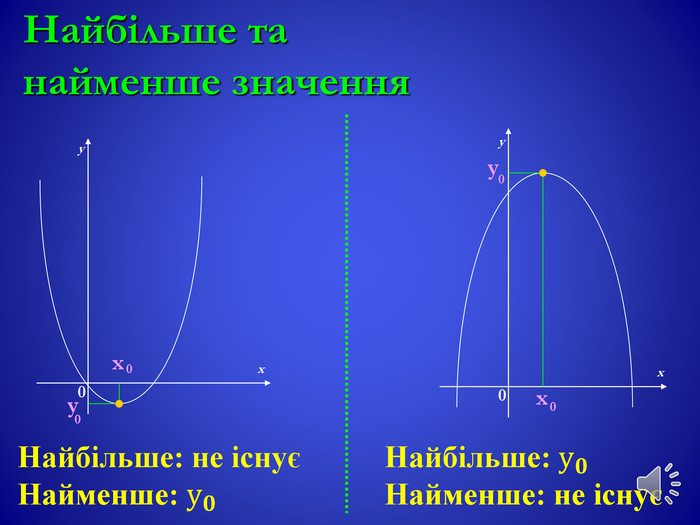
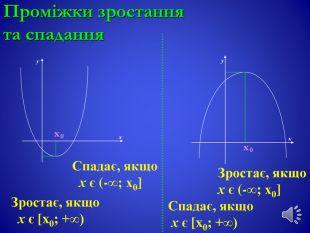
![Проміжки зростання та спаданняxx00yyxx. Спадає, якщо х є (-∞; х0]Зростає, якщо х є [x0; +∞)Зростає, якщо х є (-∞; х0]Спадає, якщо х є [x0; +∞) Проміжки зростання та спаданняxx00yyxx. Спадає, якщо х є (-∞; х0]Зростає, якщо х є [x0; +∞)Зростає, якщо х є (-∞; х0]Спадає, якщо х є [x0; +∞)](/uploads/files/364680/254257/274138_images/12.jpg)