Урок. Презентація. "Логарифмічна функція, її графік та властивості"
Про матеріал
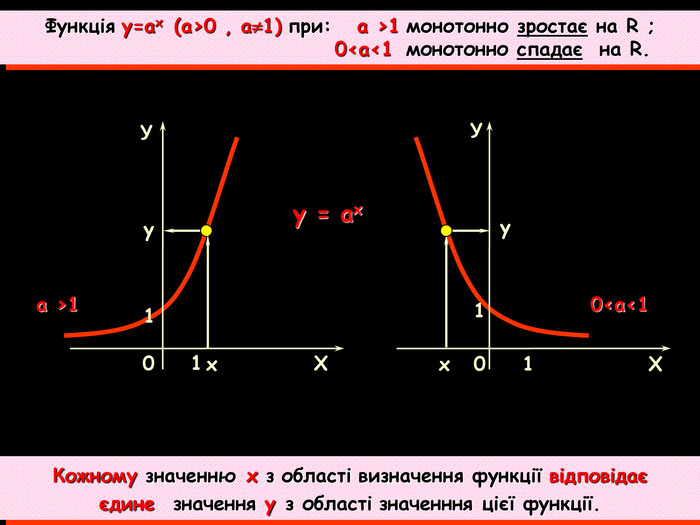
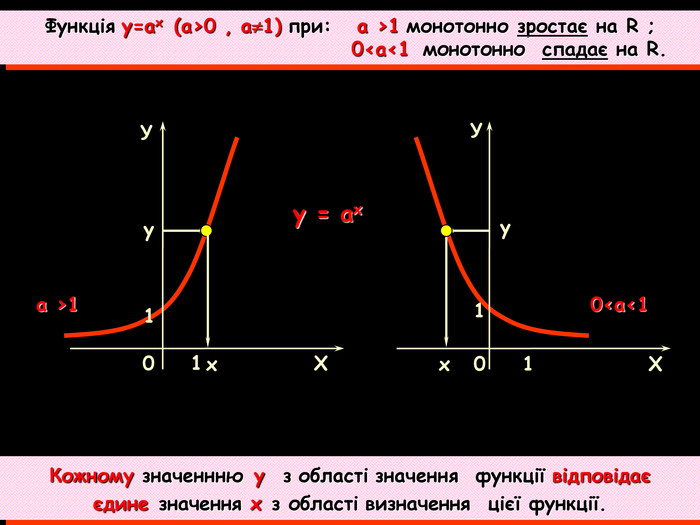
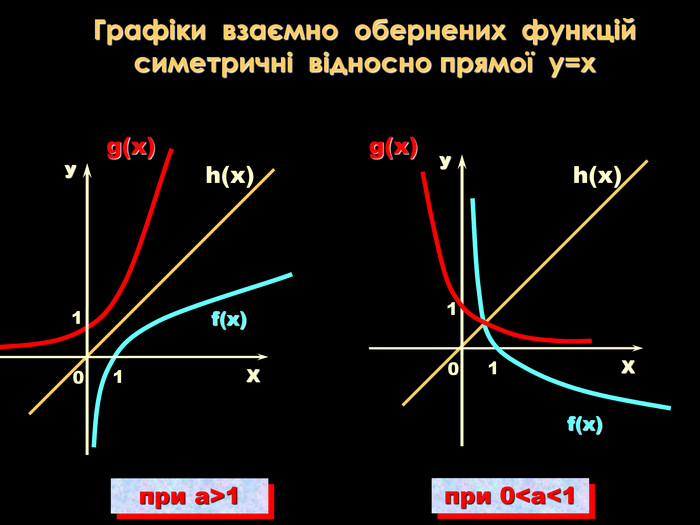
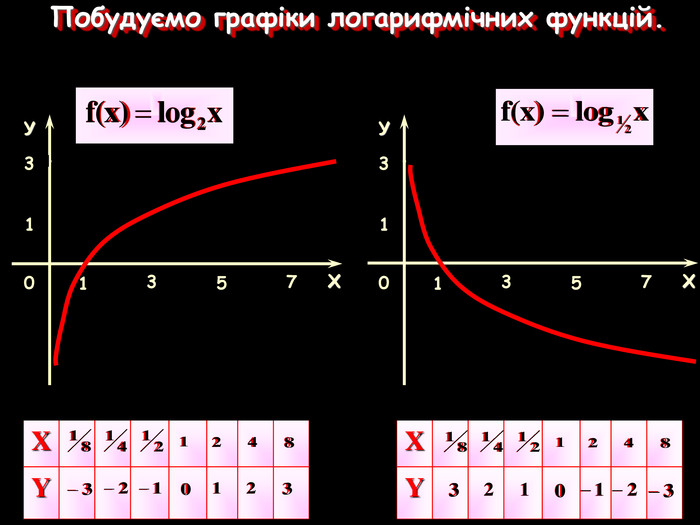
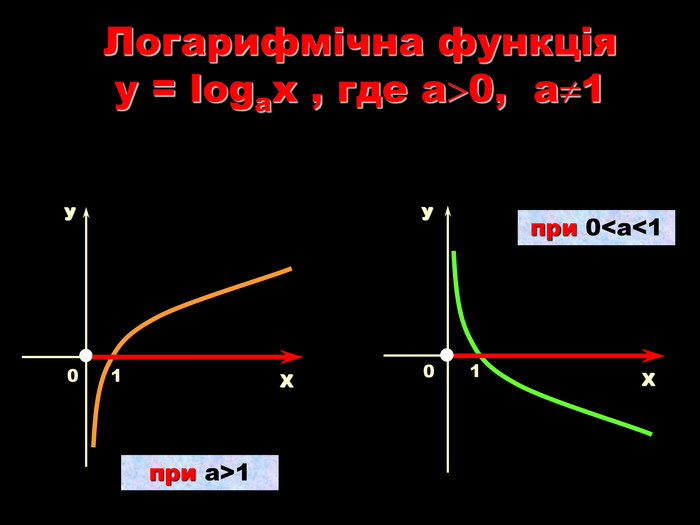
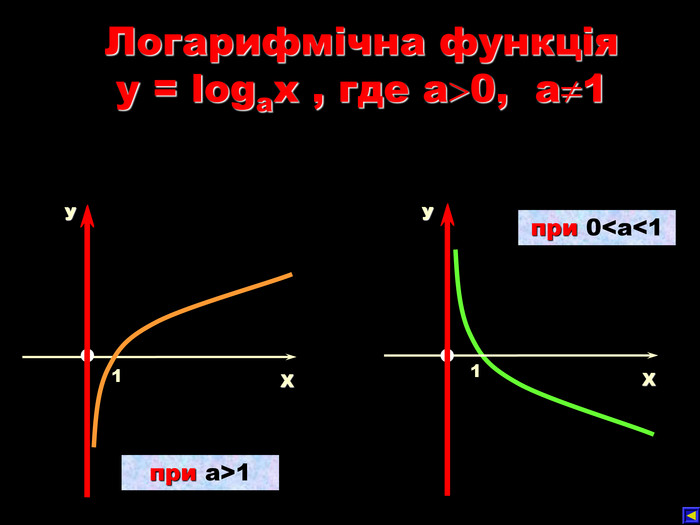
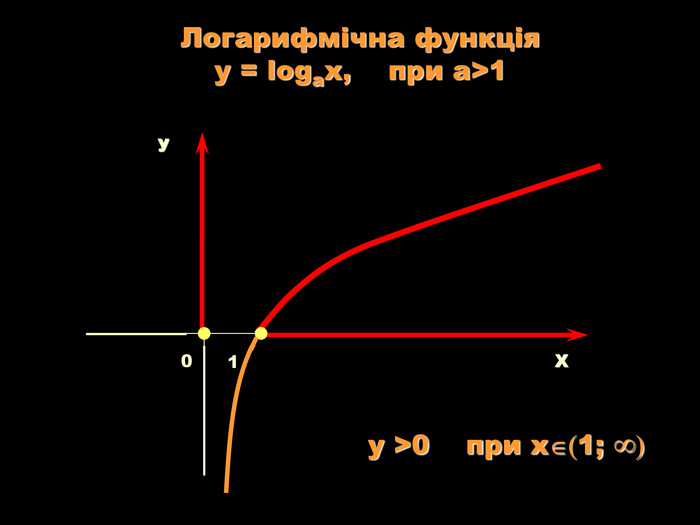
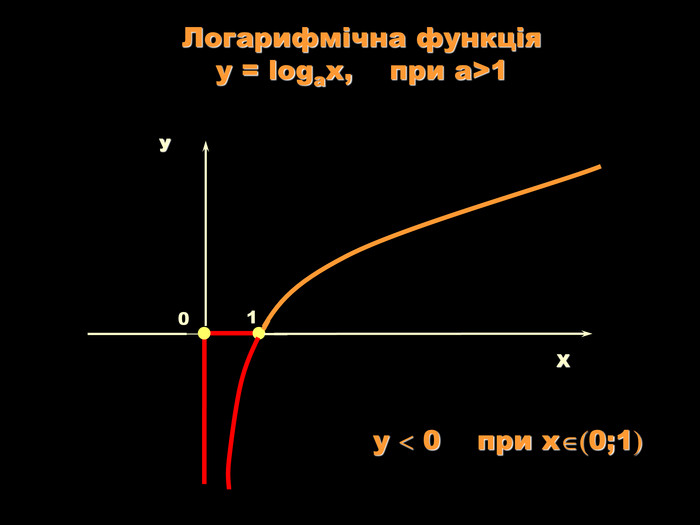
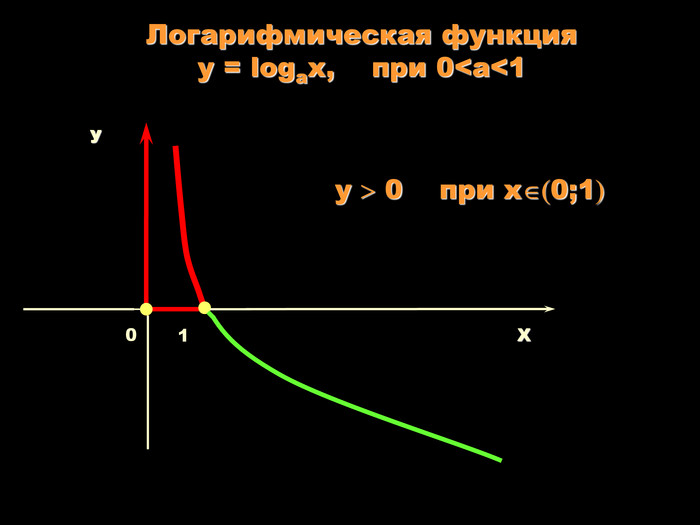
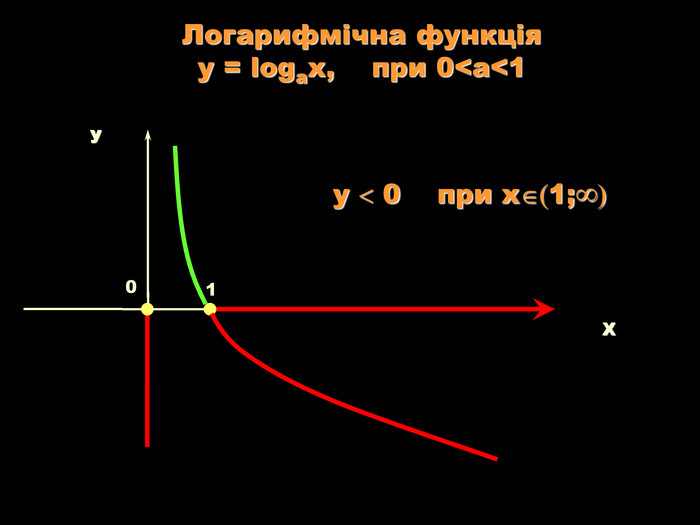
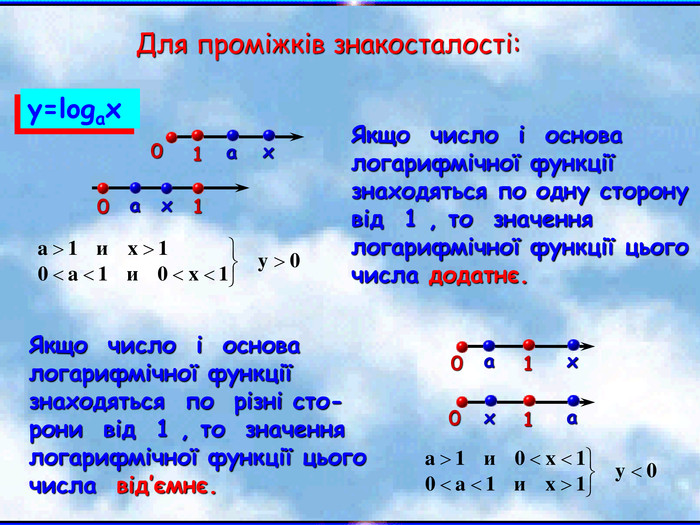
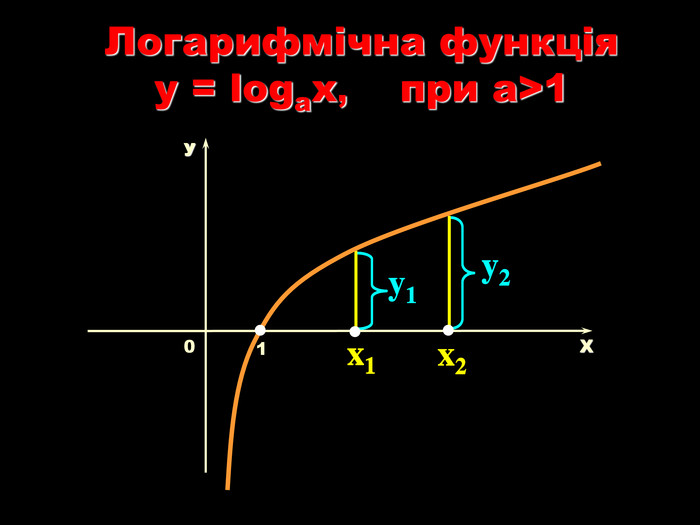
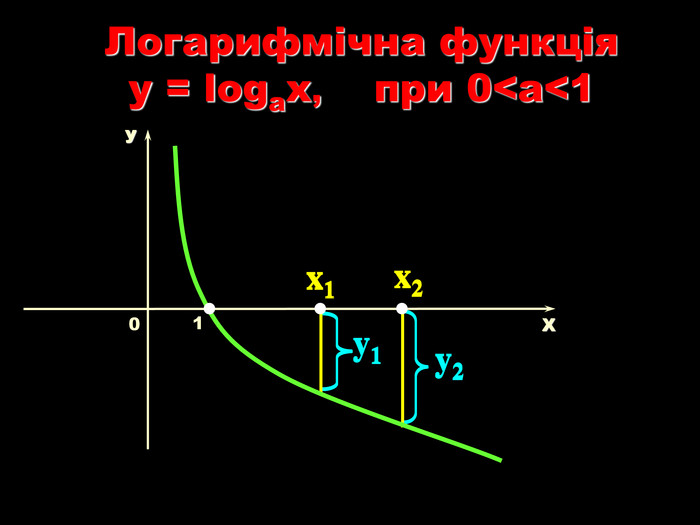
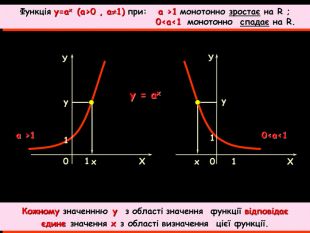
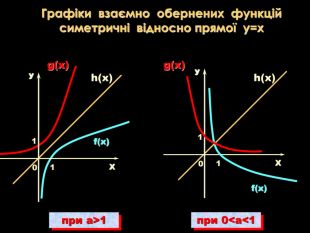
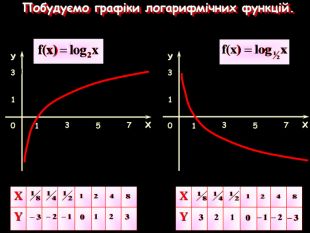
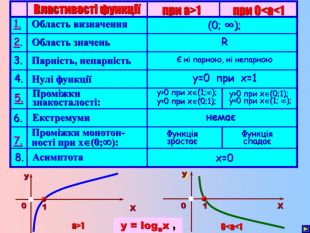
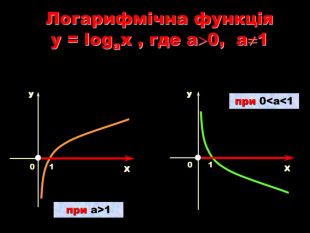
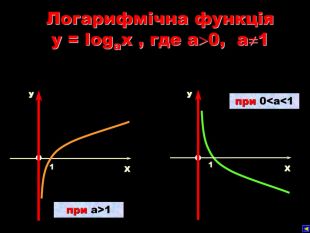
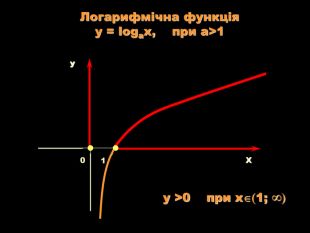
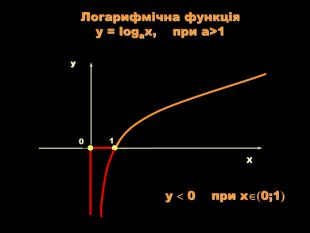
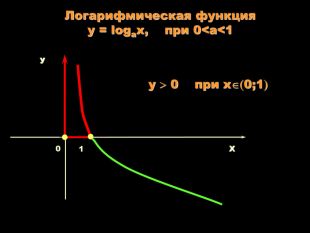
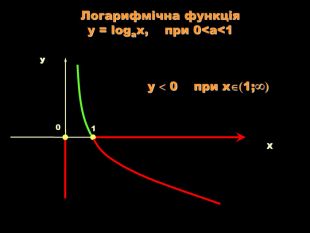
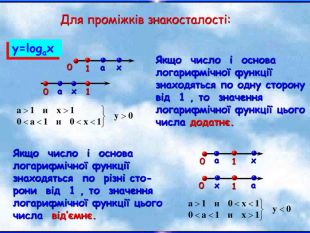
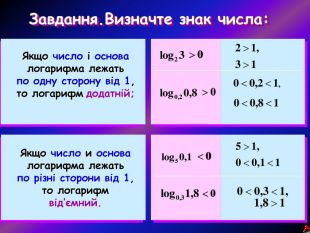
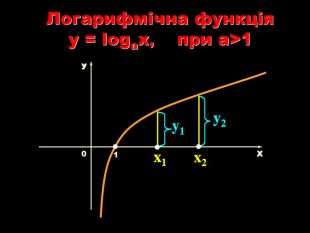
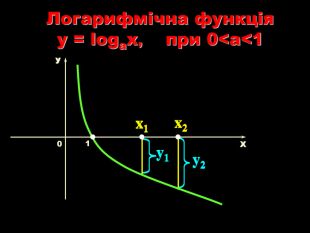
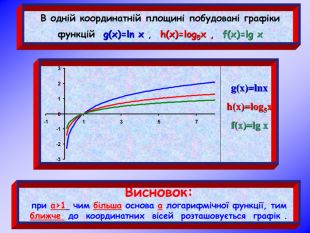
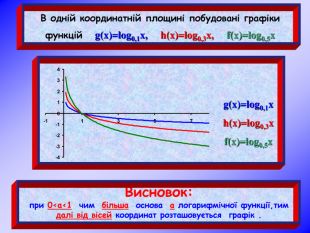
Урок на тему: Логарифмічна функція, її графік та властивості"
Мета уроку. Ознайомити учнів з логарифмічною функцією, її властивостями і графіком.
тип уроку:засвоєння нових знань
клас:11.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

















-

Перепелиця Тетяна Іванівна
10.11.2024 в 17:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лук'яненко Зоя
13.05.2024 в 09:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
01.11.2023 в 21:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горобець Ірина Вікторівна
25.11.2022 в 02:20
найкраща якісна презентація !!!! ДЯКУЮ !!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лебедева Юля
14.11.2022 в 10:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

смалько оксана
11.10.2022 в 12:17
Дуже якісна за змістом робота. Дікую автору
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Онишкевич Лора Петрівна
30.09.2022 в 10:57
Дякую за хорошу, продуману, змістовну презентацію)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лужко Олена Василівна
04.04.2022 в 10:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Личко Вікторія Михайлівна
22.02.2022 в 16:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мрачковська Олена
01.02.2022 в 10:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Назарчук Світлана Іванівна
24.02.2021 в 07:56
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Семенова Валентина Василівна
08.11.2020 в 19:31
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Нижборська Наталія
31.10.2020 в 23:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 10 відгуків