Урок з теми "Розв’язування більш складних показникових рівнянь та нерівностей"

11 клас

                                                                         Алгебра

 

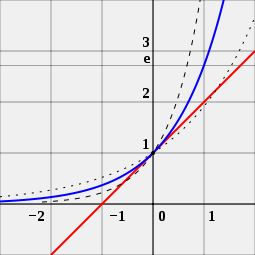e — це таке унікальне число a, при якому похідна (іншими словами тангенс кута нахилу дотичної) показникової функції f (x) = a^x (синя крива) в точці x = 0 в точності дорівнює 1. Для порівняння показані функції 2^x (точкова крива) та 4^x (пунктирна крива); тангенс нахилу їхньої дотичної відмінний від 1 (ця дотична намальована червоним)

 

 

 

 

 

 

 

 

Перед людиною є три шляхи до пізнання:

шлях мислення – найбільш благородний;

шлях наслідування –найбільш легкий;

шлях особистого дослідження – найбільш важкий.

 Конфуцій

 

Тема. Розв’язування  більш  складних показникових рівнянь та нерівностей

 

Мета уроку:    узагальнити і систематизувати знання учнів із теми  «Показникова функція»; вдосконалювати  вміння та навички розв’язування показникових рівнянь  та нерівностей  з параметрами. Розвивати  здібності учнів та креативний підхід до розв’язування  нестандартних задач та проблем,  формувати ціннісні орієнтації, вчити учнів використовувати знання в новій ситуації;  виховувати   культуру математичного мовлення                                                                                 

Тип уроку:   урок узагальнення та систематизації знань, вмінь та навичок

Обладнання:  проектор, мультимедійна дошка, підручник (А.Г. Мерзляк, В.Б. Полонський, М.С. Якір, Д.А. Номіровський  Алгебра, 11 клас) для класів з поглибленим вивченням математики.

 

Хід уроку

 

I. Організація учнів до уроку.

 

II. Актуалізація опорних знань учнів

(доцільно проводити з метою розвитку вмінь використовувати знання в нових ситуаціях)

 

Не все на світі просто, але є

Якась закономірність саме в тому,

Що істина раптово постає

Крізь ліс ускладнень, в самому простому.

Віталій Коротич

 

Фронтальна бесіда

 

1. На якому з рисунків зображено ескіз графіка функції  y =.

 

2. Встановити відповідність між функціями (1-4) та ескізами графіків (А-Д).

 

1    у =               2   у= ()^х             3    у = tg х   4  у = ctg x

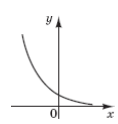
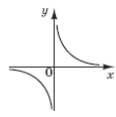
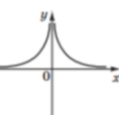
           А        Б     В   Г Д

 

 

3. На якому з графіків зображено графік функції  y = - 2|.

 

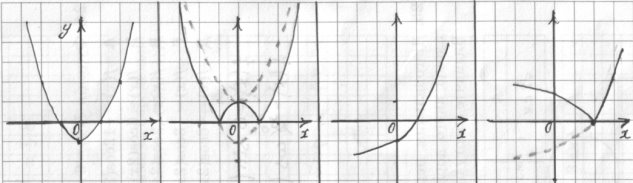
                А             Б В Г

 

 4. Знайти найменше та найбільше значення функції   у = - 1.

6. Розв’яжіть рівняння   = cosx.

 

II. Мотивація навчальної діяльності учнів

 

       На півночі є мудра притча:

«Якщо людині дати одну рибину, вона буде сита один день, якщо дати дві рибини, вона буде сита два дні, а якщо навчити людину ловити рибу, то вона буде сита все життя».

Так і в навчанні – потрібно взяти на уроці  не «заготовку» знань на завтра, а «озброїтись» вмінням здобувати ці знання та застосовувати  їх, принаймні, на  ДПА та ЗНО з математики.   А на ДПА та ЗНО  часто пропонуються задачі з параметрами. При розв’язуванні  задач з параметрами потрібно пам’ятати наступне:

- при різних значеннях параметра задача може розв’язуватись по-різному;

- при розв’язуванні нерівностей з параметром хід розв’язку може залежати від взаємного розміщення коренів відповідного рівняння;

- графічний метод (тобто аналіз властивостей функцій за допомогою зображення їх графіків при різних значеннях параметра) дозволяє полегшити аналітичні викладки.

 

III. Розв’язування вправ

 

19.35  ( застосувати метод аналізу та синтезу думок)

 

 При яких значеннях параметра  a рівняння = ах² + а²  має єдиний розв’язок?

 

Вказівка. Скористатись  графічним методом та тим, що коли це рівняння має корінь х₀ , то воно має корінь  - х₀.

Відповідь: а = -1.

 

20.30. 1) ( застосувати метод усного обговорення розв’язання)

 

 Розв’яжіть  нерівність ≥ 6 - х.

 

Вказівка. Скористатись  графічним методом або наслідком теореми про єдиний корінь.

Відповідь: х≥1.

 

19.39 ( застосувати метод мозкового штурму,  поетапне дослідження рівнянь)

 

При яких значеннях параметра  a рівняння + =+ 16  і

|a-9|· + a =1 рівносильні?

 

Вказівка. Легко встановити, що х = 0 – єдиний корінь першого рівняння. Підставимо його до другого рівняння. Маємо:| а-9|=9- а. Звідси шукані значення  параметра слід шукати серед розв’язків нерівності  а ≤ 9.

Відповідь: 0 ≤ а≤ 9  та а= -9.

 

В-10. 4 ( застосувати метод пошуку альтернативи)

 

Для кожного значення параметра  a розв’яжіть нерівність

 ( - а)

 

Відповідь: якщо а≤ 8, то  х

 якщо а>8, то   та  х = 3.

 

 

В-51. 4.1 ( застосувати метод аналогій)

 

 При яких значеннях параметра  a рівняння

 + (а – 1)· + а – 2а² = 0

 має два дійсних корені?

 

Відповідь: 0а  або а.

 

 

IV. Підсумки уроку

 

1. Оцінювання знань, вмінь і навичок учнів.

2. Висновки про вивчений навчальний матеріал з даної теми.

3. Показ фільму «Обличчя України», присвяченого М.Кравчуку( фільм триває 5 хвилин).

 

Висока наукова продуктивність і працездатність, оригінальність і гнучкість мислення видатного математика М.П. Кравчука дозволила йому отримати важливі наукові результати в алгебрі та теорії чисел, теорії функцій в диференціальних та інтегральних рівняннях. Відомо, що його науковий доробок був використаний американськими вченими при створенні першого комп’ютера. Він був  ініціатором проведення першої Київської математичної  олімпіади для школярів в 1935році. Спробуйте свої сили у розв’язанні задач цієї олімпіади.

 

V. Домашнє завдання

 

1. Спробуйте свої сили у розв’язанні двох задач першої Київської математичної  олімпіади для школярів (1935р.)

 

2. Або виконайте вправи:  19.40;  20.35.