Урок № 71 А.11 21.03.2018

Тема уроку. Логарифмічні рівняння

Мета уроку:

• навчальна: систематизувати, узагальнити знання учнів про логарифми та їх властивості, формувати вміння і навички розв’язувати логарифмічні рівняння, які зустрічаються на ЗНО, користуючись означенням та властивостями логарифма;
• розвивальна: удосконалювати навички застосовувати властивості логарифмів під час розв’язування рівнянь, які зустрічаються на ЗНО, удосконалювати розумові здібності, здатності до самостійного мислення, розвивати пам’ять, увагу;
• виховна: формувати працьовитість, прищеплювати бажання мати якісні, глибокі знання, виховувати культуру математичних записів та інтерес до вивчення предмету.

Тип уроку. Урок застосування знань, умінь та навичок.

Навчально-методичне та технічне забезпечення: Блог «Для всіх хто хоче знати математику» https://terletskyi.blogspot.com/, он-лайн тест «Показникові рівняння» та «Логарифмічні рівняння», мультимедійна презентація «Логарифмічні рівняння», мультимедійний проектор

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

1. Розв’яжіть рівняння

А. 0,5

Б. 1

В. 1,5

Г. 2

Д. 2,5

2. Розв’яжіть рівняння

А. 0

Б. 0,5

В. 1

Г. 1,5

Д. 2

3. Розв’яжіть рівняння

А. 1

Б. 0,5

В. 0

Г. 1,5

Д. 2

4. Знайдіть координати точок перетину графіка функції з віссю абсцис. У відповідь запишіть суму абсцис цих точок

5. Розв’яжіть рівняння та запишіть у відповідь його корінь. Якщо коренів кілька, то у відповідь запишіть суму коренів цього рівняння.

6. При яких значеннях параметра a рівняння має два різних дійсних корені? У відповідь запишіть найбільше ціле від’ємне значення параметра, яке не входить в множину відповідей.

Відповіді: 1 – В; 2 – В; 3 – А; 4 – 3; 5 – 7; 6 – (–1)

Коментар. Учні проходять вдома он-лайн тест «Показникові рівняння» використовуючи Google форми. Результат проходження тесту автоматично заноситься в електронний журнал, який знаходиться в Google диск.

ІІІ. Оголошення теми і мети уроку

ІV. Узагальнення навчального матеріалу

Логарифмічні рівняння містять невідому величину під знаком логарифма або в основі логарифма. Приклади логарифмічних рівнянь:

Основні методи розв’язування логарифмічних рівнянь:

• за означенням логарифма;
• за основною логарифмічною тотожністю;
• методом потенціювання;
• методом логарифмування;
• переходом до іншої основи;
• методом заміни змінної.

Особливу увагу при розв’язуванні логарифмічних рівнянь слід звернути на виконання обмежень, які накладає логарифм, тобто виконання відповідних нерівностей, або області визначення.

Коментар. Учні вдома опрацьовують Тему 8.2 «Логарифмічні рівняння» розміщену на блозі «Для всіх хто хоче знати математику» в PDF-форматі за посиланням https://drive.google.com/file/d/19PIOBGPVYXKFgZr1fpRycyK0Bs-kmFdp/view або відеолекції за посиланням https://www.youtube.com/watch?v=xfJlFAyRCMI та https://www.youtube.com/watch?v=HkCRwT4z8wY.

Перевіряється міні-конспект.

V. Розв’язування вправ

1. Якому проміжку належить корінь рівняння ?  

А	Б	В	Г	Д
(0; 2]	(2; 4]	(4; 6]	(6; 8]	(8; 10]

№ 20, 2017д

Розв’язання.

;

ОДЗ х > 0;

Відповідь: Д

 

2. Якому з наведених проміжків належить корінь рівняння ? 

А	Б	В	Г	Д
(–4; –1]	(–1; 2]	(2; 5]	(5; 8]	(8; 11]

№ 16, 2010_ІІ

Розв’язання.

ОДЗ

Відповідь: Д

 

3. Розв’яжіть рівняння .

Якщо рівняння має один корінь, запишіть його у відповіді. Якщо рівняння має кілька коренів, запишіть у відповіді їхню суму.             

№ 29, 2014

Розв’язання.

;

або

Вибір відповідної системи пов’язаний з тим, яку з нерівностей, легше розв'язати

Відповідь: –1,6

 

4. Розв’яжіть рівняння.

Якщо рівняння має один корінь, то запишіть його у відповідь; якщо воно має два корені, то у відповідь запишіть їх суму.             

№ 25, 2009

Розв’язання.

Дане рівняння рівносильне системі

Звідси

Відповідь: 12

 

5. Розв’яжіть рівняння . Якщо рівняння має один корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то у відповіді запишіть їхню суму. Якщо рівняння не має коренів, запишіть v відповіді число 100.

 № 30, 2015_І

Розв’язання.

.

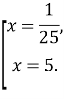
Відповідь: 5,04

6. Розв’яжіть рівняння . Якщо рівняння має єдиний корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то запишіть у відповіді їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100.             

№ 30, 2015_ІІ

Розв’язання.

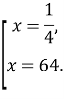
Відповідь: 64,25

Додаткові вправи

7. Знайдіть значення параметра а, при якому корінь рівняння належить проміжку  

№ 33, 2013_І

Розв’язання.

1) Значення виразу під знаком логарифма завжди додатне, отже

2) Значення кореня парного степеня завжди невід’ємне, тому:

.

3)

4) При ліва частина даного рівняння рівна нулю.

Значить, тоді і права частина даного рівняння дорівнює нулю. Маємо:

Відповідь: –14,3.

 

8. Знайдіть найменше ціле значення параметра а, при якому рівняння має корені. 

№ 32, 2007

Розв’язання.

Задане рівняння рівносильне системі

Таким чином, шуканим найменшим цілим значенням параметра а є число –3.

Відповідь: –3

VІ. Самостійна робота

1. Якому з наведених проміжків належить корінь рівняння ? 

А	Б	В	Г	Д
(–4; –1]	(–1; 2]	(2; 5]	(5; 8]	(8; 11]

№ 15, 2017п

2. Розв’яжіть рівняння  

А	Б	В	Г	Д
	3	–1	–3

№ 7, 2015_ІІ_п

3. Розв’яжіть рівняння  

А	Б	В	Г	Д
4	6	7	8	11

№ 7, 2015_І_п

4. Розв’яжіть рівняння . Якщо рівняння має єдиний корінь, то запишіть його у відповіді. Якщо рівняння має кілька коренів, то запишіть у відповіді їхню суму.              № 28, 2016п

 

5*. Розв'яжіть рівняння . Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше одного кореня, то у відповідь запишіть суму всіх коренів.              № 35, 2010_ІІ_п

 

6*. Знайдіть усі значення параметра а, при яких добуток коренів рівняння

дорівнює 8.

Якщо таке значення єдине, то запишіть його у відповідь. Якщо таких значень більше одного, то у відповіді запишіть найменше з них.              № 32, 2012п

Відповіді: 1 – Б, 2 – А, 3 – Б, 4 – 8, 5 – 10,001, 6 – 1,5

VІІ. Домашнє завдання

Опрацювати Тема 8.3, Розв’язати Тест 8.2

VІІІ. Підсумок уроку

1. Оцінювання учнів

2. систематизували, узагальнили знання учнів про логарифми та їх властивості, формували вміння і навички розв’язувати логарифмічні рівняння, які зустрічаються на ЗНО, користуючись означенням та властивостями логарифма.