Урок-проект з геометрії для 7 класу на тему "Країна трикутників"

Урок-проект з геометрії для 7 класу

 

Тема уроку: Країна трикутників

 

Мета уроку

Освітня:

• Узагальнити знання про трикутники: означення трикутника, означення прямокутного трикутника, сума кутів трикутника, сума гострих кутів прямокутного трикутника, види трикутників за його кутами, визначні точки трикутника.
• Формувати навички та уміння  практичного  використання набутих теоретичних знань, розвивати творчі здібності і логічне мислення учнів при знаходженні ними раціональних шляхів для розв’язування практичних задач.
• Формувати організаційну, соціально-особистісну, інформаційну, життєтворчу компетентності.
• Сформувати уявлення учнів про геометричну фігуру - трикутник, як невід'ємну частину навколишнього нас світу, про різне використання в побуті й життя предметів і обладнань, що мають форму трикутника, про значимість даного поняття в соціальному житті людини.
• Показати зв'язок математики із повсякденним життям, зв'язок з другими науками: географія, фізика, музика, архітектура тощо.

Розвивальна:

• Сприяти розвитку самоосвітньої діяльності учнів; інтересу до проектної діяльності; розвитку предметної та життєво необхідної компетентностей.

Виховна:

• Виховувати культуру спілкування; культуру усного мовлення; любов до предмету.

 

Тип уроку: узагальнення й систематизації знань.

 

Технологія проведення уроку: проектна (захист проекту).

 

Інноваційна ідея уроку: метод проектів – засіб продуктивного  навчання на уроці узагальнення й систематизації знань.

 

Методи проведення уроку:

• Словесні - розповідь, бесіда.
• Наочні - демонстрація виконаних презентацій, публікації, відеофільм та ін.

Хід уроку

I. Організаційний момент (1 хв.)

Вчитель.

Добрий день, діти. Радий вас бачити.

Чи ви хочете дізнатись

Що сьогодні має статись?

Тож, сідаємо рівненько –

Попрацюємо гарненько!

Прикрили очі й подумки сказали: "На уроці наші очі уважно дивляться й усе бачать. Вуха чуйно слухають і все чують. Голова добре працює".

Я бажаю вам успіху, а ви побажайте мені удачі!

 

II. Мотивація навчальної діяльності учнів (2 хв.)

Вчитель:

Багатьом відома така притча.

Звернувся до ченця бідняк:

- Дай мені рибу. Я голодний.

Чернець мовчки віддав вудку.

Повчальний характер притчі зрозумілий: треба давати не стільки їжу, скільки спосіб її добувати.

Мені здається, що цей висновок також стосується цілей і завдань, які ми з вами поставили перед собою, розпочавши роботу над проектом «Країна трикутників».

Кожен етап роботи над проектом важливий, але найважливішим, звичайно, є заключний етап. Саме на цьому етапі кожен з вас може побачити і оцінити результати своєї праці. Усвідомити, чого ви навчились і яких знань і умінь вам бракує. Чому б ви хотіли навчитися у майбутньому, а також поділитися своїми здобутками з товаришами.

На сьогоднішньому уроці ми будемо відпрацьовувати вміння об’єктивно оцінювати свою роботу і роботи товаришів, а також публічно захищати свій проект.

 

ІІІ.    Актуалізація знань. Теоретична розминка (5 хв.)

Вчитель:

Тож, запрошую до активної роботи. Хочу звернути вашу увагу на розташовані на столах аркуші, де знаходяться ті завдання нашого уроку, які вам доведеться виконувати. Насамперед, давайте згадаємо деякі поняття з геометрії. Я підготував для вас кросворд. Ваше завдання: вписати слова й відгадати ключове слово по вертикалі.

 

 

 

 

КРОСВОРД «ТРИКУТНИКИ»

(7 клас)

 

 

 

 

 

 

 

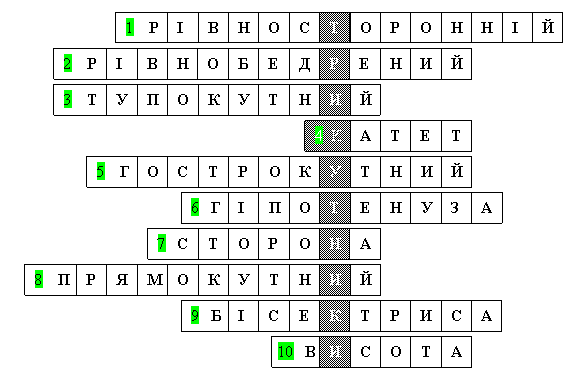
1. Трикутник, усі сторони якого рівні.
2. Трикутник, дві сторони якого рівні.
3. Трикутник, один із кутів якого 105°.
4. Одна зі сторін прямокутного трикутника.
5. Трикутник, найбільший кут якого гострий.
6. Сторона трикутника, що лежить проти прямого кута.
7. Відрізок, що сполучає вершини трикутника.
8. Трикутник, один із кутів якого 90°.
9. Висота рівностороннього трикутника також і … .
10. Відрізок, проведений з вершини трикутника перпендикулярно до прямої, яка містить протилежну сторону.

 

Отже, ключове слово – Трикутники.

Трикутник… Чудова геометрична фігура і найпопулярніша в шкільній програмі з геометрії.

Багато хто думає, що трикутники «оселилися» тільки на сторінках підручника і більше їх ніде побачити? Чи так це насправді?

Сьогодні ви здійсните подорож «Країною трикутників» і я сподіваюсь отримаєте відповідь на це питання.

 

 

 

ІV.    Формулювання теми і задач уроку (3 хв.)

Вчитель.

Отже, тема сьогоднішнього уроку – «Країна Трикутників». Урок цей буде незвичайний. Це урок – свято, урок захисту учнівських проектів. Девізом нашого уроку стануть слова видатного педагога Я. А. Коменського «В особистій практиці сховані таємниці швидких і надійних успіхів».

Сьогодні ми закінчуємо вивчення теми «Трикутники». Впродовж теми ви об’єдналися в 4 групи: «Теоретики», «Практики», «Дослідники» і «Пошуковці», працювали над своїми проектами і ось настав момент істини – звітуватися про виконану роботу.

Сподіваюся, на уроці ви:

• розширите ваші знання про трикутник та його елементи;
• формуватимете практичні навички розв’язування задач;
• будете розвивати вміння співпрацювати в групах, проявляти ініціативу, робити  висновки;
• зумієте сформувати на уроці атмосферу творчого пошуку, пізнавальної діяльності і самостійності.   

Отже, розпочнемо захист проектів. Прошу при цьому не забути про те, що усяка діяльність людини повинна бути оцінена. І сьогодні, під час проведення захисту проектів, вам необхідно буде оцінити виступ своїх товаришів. Критерії оцінювання ми з вами обговорювали на попередньому уроці. Тому уважно слухаємо виступ своїх однокласників і після нього виставляємо свою оцінку в бланк оцінювання, який ви здасте мені наприкінці  уроку.

Першою свої здобутки на ваш розсуд представить група «Теоретики», тож давайте надамо їй слово.

 

V. Захист учнівських проектів (25 хв.)

Звіт групи «Теоретики»

 

Керівник групи:

Ми – група Теоретики (разом).

Девіз групи: (разом)

Теорію трикутників будемо вивчати,

Щоб легко було задачі про них розв’язати.

Завдання, яке було поставлене перед нами: систематизувати теоретичний матеріал з теми «Трикутник» і представити результат своєї роботи в вигляді інформаційного бюлетеня.

Розпочнемо звіт групи парадом трикутників.

(Члени групи тримають у руках плакати, на яких зображені трикутники: рівносторонній, рівнобедрений, гострокутний, тупокутний, прямокутний. Керівник групи називає трикутники за сторонами і кутами, а учні, які показують власне трикутники, дають означення трикутників і формулюють їх властивості.)

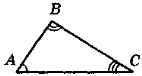1. Трикутник

 

Учень 1:

Трикутником називають  фігуру, яка складається з трьох  точок,  що  не  лежать  на одній  прямій,  і  трьох відрізків, які сполучають ці точки. Основні елементи трикутника:

1. Вершини (А, В, С)
2. Сторони (АВ, ВС, АС)
3. Кути (А,  В, С)

Сума довжин сторін трикутника називається периметром, позначається буквою Р.

Сума кутів будь-якого трикутника дорівнює 180.

Для будь-якого трикутника виконується так звана нерівність трикутника – сума будь-яких двох сторін трикутника більше третьої сторони.

У трикутнику проти більшої сторони лежить більший кут і навпаки проти більшого кута лежить більша сторона.

 

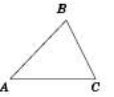2. Гострокутний трикутник

 

Учень 2:

Трикутник, у якого всі кути гострі, називається гострокутним трикутником.

 

3. Прямокутний трикутник

 

Учень 1:

Трикутник, у якого один кут прямий, а два інші – гострі, називається прямокутним трикутником.

Сторона, яка лежить проти прямого кута, називається гіпотенузою. Сторони, що утворюють прямий кут, називаються катетами.

Сума гострих кутів прямокутного трикутника дорівнює 90.

У прямокутному трикутнику з кутом  30 катет, протилежний цьому куту, дорівнює половині гіпотенузи.

 

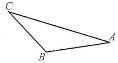4. Тупокутний трикутник

 

Учень 2:

Трикутник, у якого один кут тупий, а два інші – гострі, називається тупокутним трикутником.

 

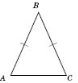5. Рівнобедрений трикутник

 

Учень 1:

Трикутник називається рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються бічними сторонами, а третя сторона — основою трикутника.

У рівнобедреному трикутнику кути при основі є рівними.

 

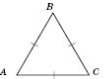6. Рівносторонній трикутник

 

Учень 2:

Трикутник, у якого всі сторони рівні, називається рівностороннім трикутником.

У рівностороннього трикутника всі кути рівні, кожний дорівнює 60.

 

Керівник групи:

Вся геометрія з часів «Начал» Евкліда спирається на «трьох китах» - трьох ознаках рівності трикутників. Давайте їх пригадаємо (відповідають учні).

 

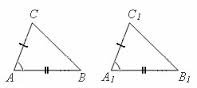
Перша ознака рівності трикутників — за двома сторонами й кутом між ­ними.

Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.

 

Учень 1:

 

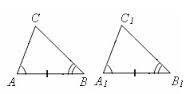
Друга ознака рівності трикутників — за стороною й прилеглими до неї ку­тами.

Якщо сторона й прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні.

 

Учень 2:

 

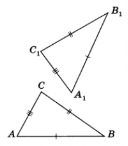
Третя ознака рівності трикутників — за трьома сторонами.

Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні.

 

Керівник групи:

А тепер ми хотіли б запропонувати усні вправи на застосування ознак рівності трикутників. (Завдання підготовлені на інтерактивній дошці у вигляді відривного календаря, листками якого є картки-плакати з задачами).

Завдання полягає в наступному: потрібно вказати рівні трикутники та ознаку їх рівності.

(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

 

 

 

Відповіді учнів:

 

                                                    

 

 

 

 

 

 

 

 

 

 

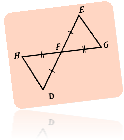
 HFD =  GFE за першою ознакою, оскільки FH = FG, FD = FE,  HFD = GFE (як вертикальні кути).

                                                                                                                         

 

 

 

 

 

 

 

 

 

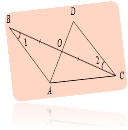
 ABO =  DCO за другою ознакою, оскільки ВО = ОС,  В =  С,  АОВ = DOC (як вертикальні кути).

 

 

                                                    

 

 

 

 

 

 

 

 

 

 

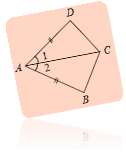
 ABC =  ADC за першою ознакою, оскільки AB = AD, AC – спільна сторона,  DAC =  BAC.

    

 

 

 

 

 

 

 

 

 

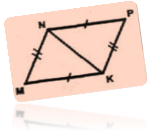
 KMN =  NPK за третьою ознакою, оскільки KM = NP, MN = KP, KN – спільна сторона.

                                                    

 

 

 

 

 

 

 

 

 

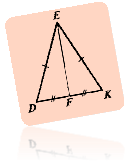
 DFE =  KFE за третьою ознакою, оскільки DE = EK, DF = FK, EF – спільна сторона.



 

 

 

 

 

 

 

 

 

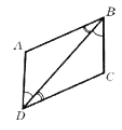
 ABD =  BCD за другою ознакою, оскільки  ADВ =  СBD,  АВD = CDB, BD – спільна сторона.

 

Керівник групи:

Трикутник є найперша фігура, яка не може розкластися в інший вид більш простих фігур і тому є першим фундаментом будь-якої речі, що має межу і фігуру.                                                                                                                                Д. Бруно

 

Звіт групи «Теоретики» завершено. Дякуємо всім за увагу та плідну роботу.

 

Вчитель:

Дякуємо групі «Теоретики» за змістовну роботу та гарний захист проекту. Сідайте, будь ласка, на свої місця. Прошу оцінити роботу групи за критеріями, які знаходяться в оцінюючому листі.

(Капітани груп «Практики», «Дослідники», «Пошуковці» виставляють оцінки групі «Теоретики»).

 

Вчитель:

Слово для захисту проектної роботи надається групі «Практики».

 

Звіт групи «Практики»

(Учні виходять  до  дошки, між двома з них відбувається діалог про те, як вони розв’язують задачі).

 

Перший учень:

- Не знаю як ти, а я знавець!

Як берусь я до задачі,

То не стогну і не плачу.

І для мене не проблема 

Найскладніша теорема!

Чи це так , чи може ні

Це судити не мені...

 

Другий учень

- А у мене все навпаки,

Як берусь я до задачі,

То над нею зразу плачу.

Як вивчаю аксіому,

То в спині у мене ломить.

Чи знавець, а чи ні –

Це судити не мені...

 

Третій учень

Якщо хочеш досягнути 

У житті своїх вершин –

Математику збагнути

Мусиш тонко, до глибин!

 

Керівник групи:

Ми – група «Практики». (разом)

Наша група працювала під девізом: «Найдосконаліший мозок іржавіє без дії». (разом)

Мета, яка стояла перед нами – це систематизувати та узагальнити теоретичні знання з теми «Трикутник» в задачах.

Завдання: опрацювати підручник, збірники задач, Інтернет, підібрати задачі та продумати оформлення.

Результатом нашої роботи стала книжка-збірник задач із теми «Трикутник», яку ми хочемо зараз вам презентувати. До цієї книжки ми включили різноманітні задачі. Це – кількісні задачі, задачі за готовими малюнками, проблемні питання, задачі практичного змісту та ін.

Деякі з задач, включених до книжки, ми хочемо запропонувати вам.

 

Учень 1:

Задача 1 (2 б.)

 

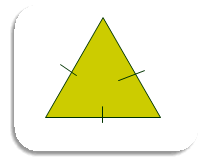
Периметр трикутника дорівнює 27 см. Знайдіть сторони цього трикутника.

(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

Відповідь: Трикутник, зображений на малюнку, рівносторонній. Його периметром є сума трьох рівних сторін. Тому, аби знайти сторону цього трикутника, потрібно периметр поділити на 3. Отже, сторони трикутника дорівнюють 9 см.

 

Учень 2

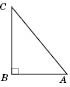
Задача 2 (1 б.)

 

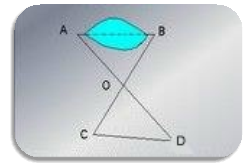
Яку ознаку рівності використали, щоб виміряти відстань між пунктами A і В?

(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

Відповідь:  Дана задача є типовою практичною задачею в темі «Ознаки рівності трикутників. Щоб виміряти відстань між пунктами А і В потрібно скористатися першою ознакою рівності трикутників, оскільки практичними діями того, хто цю задачу розв’язував на місцевості, було створено умови виконання даної ознаки, а саме: АО = ОD, ВО = ОС,  АОВ =         СОD.

 

Учень 3:

Задача 3 (1 б.)

Чи існує трикутник зі сторонами: 1) 2 дм, 5 дм і 7 дм; 2) 2 см, 3 см і 6 см; 3) 5 дм, 2 дм і 4 дм?
(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

Відповідь: Для існування трикутника з певними сторонами необхідно, щоб виконувалася нерівність трикутника, а саме: будь-яка сторона повинна  бути меншою за суму двох інших сторін. Ця умова виконується тільки у третьому випадку. В перших двох випадках трикутник існувати не буде.

Учень 1:

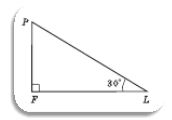
Задача 4 (1 б.)

Кут  L прямокутного трикутника PFL дорівнює  30°. Знайдіть PF, якщо PL = 16 дм.

 

(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

Відповідь: У прямокутного трикутника з кутом 30 катет, протилежний цьому куту, дорівнює половині гіпотенузи. Тому PF = 16 : 2 = 8 дм.

 

Учень 2:

Задача 5 (2 б.)

Приведіть у відповідність назву лінії трикутника з малюнком, на якому ця лінія зображена. 

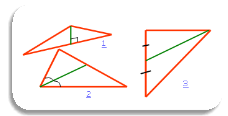 А. висота

 Б. медіана

 В. бісектриса

 

(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

Відповідь:  А1 (відрізок із вершини трикутника до протилежної сторони проведений під прямим кутом);

                      В2 (відрізок, проведений із вершини трикутника до протилежної сторони, ділить кут навпіл);

                          Б3 (відрізок, проведений із вершини трикутника, ділить протилежну сторону на два рівні відрізки).

 

Учень 3:

Задача 6 (2 б.)

Кут при основі рівнобедреного трикутника дорівнює 72°. Знайдіть кут при вершині.

(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

Відповідь:  У рівнобедреного трикутника кути при основі рівні, тому, щоб знайти кут при вершині, потрібно застосувати теорему про суму кутів трикутника. Маємо 180 - 72 - 72 =  36. Отже, кут при вершині рівнобедреного трикутника = 36.

 

Учень 1:

Задача 7 (3 б.)

 

 

 

 

 

 

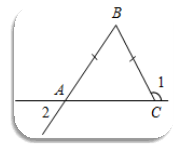
Дано: АВ = ВС, 1 = 130°. Знайти 2.

(Керівник групи вибирає відповідаючого з учнів, які підняли руку).

 

Відповідь:  1 є зовнішнім кутом для  С АВС, тому  С = 180 - 130 = 50.  АВС – рівнобедрений, тому  А = 50, оскільки  А і  С – кути при основі.  А і 2 – вертикальні кути, отже  2 =  А = 50.

 

Керівник групи:

Щоб творити потрібну справу,

Щоб у житті не траплялось невдач,

В похід ми відправились сміливо,

В світ загадок і складних задач.

І не біда, що йти було далеко,

Не страшно, що дороги ці були важкі.

Досягнення й великим людям

Ніколи не були легкі.

Звіт групи «Практики» завершено. Дякуємо всім за увагу та плідну роботу.

 

Вчитель:

Дякуємо групі «Практики» за змістовну роботу та гарний захист проекту. Сідайте, будь ласка, на свої місця. Прошу оцінити роботу групи за критеріями, які знаходяться в оцінюючому листі.

(Капітани груп «Теоретики», «Дослідники», «Пошуковці» виставляють оцінки групі «Практики»).

 

Вчитель:

Діти, ми заслухали звіти двох груп і, напевно, втомилися. Тож, давайте відновимо сили. Запрошую вас на фізкультхвилинку.

 

Фізкультхвилинка

 

Вчитель:

Молодці. Сідайте, будь ласка. Продовжуємо. Слово надається групі «Пошуковці», яка підготувала для вас віртуальну екскурсію країною трикутників.

 

Звіт групи «Пошуковці»

 

Керівник групи:

Ми група - «Пошуковці». (разом)

Наш девіз:

 

Учень 1:

 «Музика може возвеличити або заспокоїти душу,

 

Учень 2:

Живопис – радувати око,

 

Керівник групи:

Поезія – пробуджувати почуття,

 

Учень 1:

Філософія – задовольняти потреби розуму,

 

Учень 2:

Інженерна справа – удосконалювати матеріальну сторону життя людей,

 

Всі разом:

А математика здатна досягти усіх цих цілей».

Американський математик Моріс Клайн

 

Керівник групи:

Мета роботи: дослідити, де в житті можна зустріти трикутники?

Завдання: опрацювати інформаційний матеріал, ресурси Інтернету, енциклопедії, систематизувати матеріали, застосувати до теми уроку.

Починаючи роботу над проектом, ми навіть не очікували, що зустрінемо трикутник у самих несподіваних місцях. Де саме, ви зрозумієте, переглянувши відеофільм, створений нами під час проекту. Отже, увага на дошку.

 (перегляд фільму)

 

Керівник групи:

Працюючи над проектом, ми дійшли розуміння того, що практично скрізь присутня геометрична фігура – трикутник. З цього слідує логічний висновок: «З трикутником пов’язана не лише наука математика, але й наше повсякденне життя».

Звіт групи «Пошуковці» завершено. Дякуємо всім за увагу.

 

Вчитель:

Дякуємо групі «Пошуковці» за змістовну роботу та гарний захист проекту. Сідайте, будь ласка, на свої місця. Прошу оцінити роботу групи за критеріями, які знаходяться в оцінюючому листі.

(Капітани груп «Теоретики», «Дослідники», «Практики» виставляють оцінки групі «Пошуковці»).

 

Вчитель:

Слово для захисту проектної роботи надається групі «Дослідники».

 

Звіт групи «Дослідники»

Керівник групи:

Шановні однокласники. Пропонуємо вашій  увазі дослідницький проект «Визначні точки і лінії трикутника»

Мета проекту:

1. дослідити, чи залежить єгипетський трикутник від довжини його сторін;
2. довести справедливість рішень задач Наполеона, Морлі;
3. дослідити визначні точки трикутника - точки перетину висот, медіан, бісектрис трикутника.

Результат своєї роботи ми повинні були представити в вигляді презентації.

Отже, увага на інтерактивну дошку.

 

Учень 1:

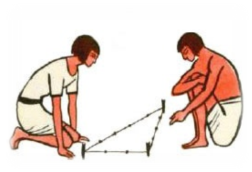
У Прадавній Греції був відомий спосіб побудови прямокутного трикутника на місцевості. Для цього використовували мотузку, на якій було нав'язано 13 вузликів, на однаковій відстані один від одного. Давайте й ми  спробуємо побудувати прямокутний трикутник. От бачите, незважаючи на те, що мотузки були різної довжини, принцип побудови в усіх однаковий: одна сторона містить 3 відрізка, інша - 4 відрізка, третя - п'ять.

Саме цей принцип побудови прямокутних трикутників використовувався при будівництві пірамід у Єгипті. Напевно, тому прямокутний трикутник зі сторонами 3, 4, 5 і назвали єгипетським трикутником.

 

 

 

Учень 2:

Ще більш дивним було відкриття, зроблене американським математиком Ф. Морлі. Він довів, що якщо в трикутнику через вершини провести  промені, що ділять кути на три рівні частини, то точки перетинання суміжних трисектрис є вершинами рівностороннього трикутника.

 

 

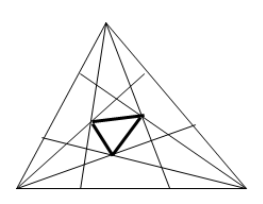
Виконуючи побудови трисектрис для різних видів трикутників, ми довели, що теорема Морлі справедлива!!!

 

Учень 3:

Геометрія настільки цікава наука, що нею в різні часи займалися не тільки вчені, а й прості громадяни. Хоча, людину, теорему якого ми досліджували, простим громадянином і назвати неможна, адже це - Наполеон Бонапарт, який з’ясував, що якщо на кожній стороні довільного трикутника побудувати по рівносторонньому трикутникові, то трикутник з вершинами в центрах рівносторонніх трикутників - теж рівносторонній.

 

 

 

 

 

 

 

 

Багатьма побудовами й вимірюваннями ми довели, що це насправді виконується для будь-якого довільного трикутника.

 

Учень 1:

Якщо вершину кута з’єднати із серединою протилежної сторони, то цей відрізок називається медіаною трикутника. Оскільки у трикутника три кута і три сторони, то медіан буде три й усі вони перетинаються в одній точці, причому в цій точці вони діляться в відношенні 2:1.

 

 

 

 

 

 

 

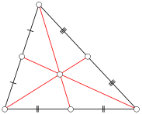
У підсумку ми отримали першу визначну точку трикутника: точку перетину медіан, яка називається центроїдом трикутника.

 

Учень 2:

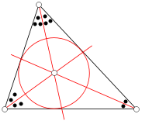
Якщо в трикутнику провести бісектриси кутів, то вони теж будуть перетинатися в одній точці.

У підсумку ми отримали другу визначну точку трикутника: точку перетину бісектрис трикутника – центр вписаного в трикутник кола.

 

 

 

 

 

 

 

Учень 3:

Аналогічно, якщо провести висоти трикутника, тобто перпендикуляри, проведені із вершин трикутника до протилежних сторін, то їх теж буде три і всі вони також перетинаються в одній точці.

 

 

 

 

 

 

 

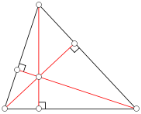
У підсумку ми отримали третю визначну точку трикутника: точку перетину висот трикутника – ортоцентр.

 

Керівник групи:

Ми з дитинства були знайомі з геометричною фігурою, яка має назву трикутник. Але небагато про нього знали. Працюючи над проектом «Країна трикутників» ми поглибили свої знання про трикутник, більше дізналися про вчених, які зробили великий внесок у розвиток вчення про трикутник, дослідили визначні точки трикутника. Сподіваємося, що подальше вивчення геометрії надасть нам можливість пізнати трикутник ще більш детальніше.          

Звіт групи «Дослідники» завершено. Дякуємо всім за увагу.

 

Вчитель:

Дякуємо групі «Дослідники» за змістовну роботу та гарний захист проекту. Сідайте, будь ласка, на свої місця. Прошу оцінити роботу групи за критеріями, які знаходяться в оцінюючому листі.

(Капітани груп «Теоретики», «Пошуковці», «Практики» виставляють оцінки групі «Практики»).

 

 

 

 

VІ. «Ключовий момент» (оцінювання результатів роботи над проектами).

Вчитель:

Всі групи представили свої проекти, тож підведемо підсумки нашої роботи.

Шановні учасники проекту! Ви плідно попрацювали, зробили дуже багато, багато цікавого дізналися. Ми проглянули різні роботи. Всі  показали високий рівень знання інформаційних технологій і уміння застосовувати їх при виконанні завдань практичного вмісту. Ніхто з учнів не віднісся до роботи байдуже, всі брали активну участь в дослідницькій роботі при розробках проектів. В подальшому ваше завдання полягатиме розмістити на блозі наш проект. Дякую усім групам за цікаві проекти.

Ось і закінчився наш проект.

Час невпинно й швидко так летить.

Ви до знань зробили новий крок.

Хай у всьому завжди вам щастить!

Дякую, що працювали гарно,

Часу ви не витрачали марно,

Свої сили і знання доклали.

І проект свій склали.

 

VІІ.    Домашнє завдання.

Домашнє завдання буде творчим і вибрати тип роботи ви зможете самостійно.

1. Скласти сенкан до слова Трикутник.
2. Скласти асоціативний кущ до слова Трикутник.
3. Написати вірш або казку про Трикутник.
4. Спробуйте розрізати рівносторонній трикутник на п’ять рівнобедрених.
5. Створити мозаїку, аплікацію чи малюнок, використовуючи різні види трикутників.

 

VІІІ.    Підсумок уроку.

(вручання грамот і коментоване виставлення оцінок вчителем)

 

Урок уже закінчено.

Нам можна далі йти

І до нової теми

В програмі перейти.

Всі добре працювали,

Старались як могли.

Немає переможених,

Тут всі перемогли.

Наш урок підійшов до свого логічного завершення. Усім спасибі. До побачення. Виходячи з кабінету, оцініть, будь ласка, свій настрій після уроку.

 

Рефлексія