Урок "Рівність геометричних фігур"

Тема: РІВНІСТЬ ГЕОМЕТРИЧНИХ ФІГУР

Мета:

Навчальна:

• дати означення рівних фігур, рівних трикутників,
• навчити знаходити пари рівних відповідних елементів трикутників; застосувати означення рівності трикутників під час розв’язування задач;
• застосовувати означення рівності трикутників під час розв’язування задач;

Розвивальна:

• розвивати просторову уяву та логічне мислення, уміння грамотно висловлювати свою думку, вміння наводити приклади рівних фігур, знаходити по запису рівних трикутників пари рівних елементів;

Виховна:

• виховувати культуру геометричної мови, інтерес до предмету, охайно вести свої записи й виконувати креслення, уміння об’єктивно оцінювати свої сили.

Тип уроку: урок засвоєння нових знань

ХІД УРОКУ

І. Організаційний етап

Перевірка готовності учнів до уроку.

ІІ. Перевірка домашнього завдання

Учні-консультанти перевіряють наявність і правильність виконання домашнього завдання в зошитах.

Учитель перевіряє «творче домашнє завдання».

Як за допомогою лінійки побудувати кут рівний даному?

ІІІ. Актуалізація опорних знань. Оголошення теми та мети уроку

Учні розв’язують кросворд, в якому з’являється тема уроку - «РІВНІСТЬ».

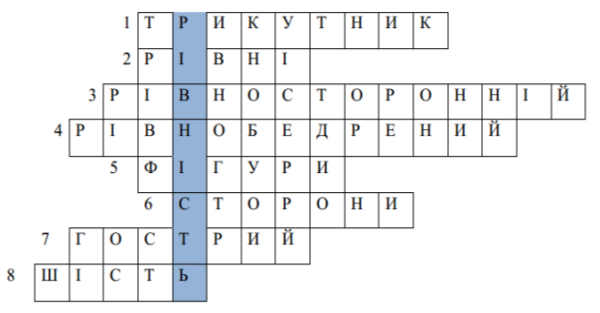
Запитання до кросворду:

1. Фігура, яку почали вивчати на попередньому уроці.

2. Якщо два відрізка мають однакова довжину, то вони…..

3. У трикутника всі сторони рівні.

4. У трикутника дві сторони рівні.

5. Їх вивчає геометрія.

6. Їх у трикутника три.

7. Кут, міра якого менша за 90º.

8. Периметр рівностороннього трикутника дорівнює 18 см. Яка довжина його сторони?

ІV. Мотивація навчальної діяльності

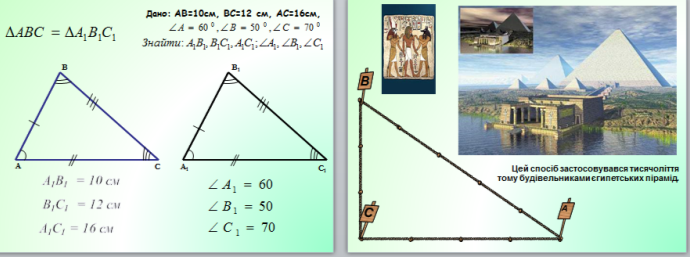
Перші відомості про трикутник та його властивості ми знаходимо в єгипетських папірусах, яким більше 4000 років. У них, зокрема, згадується спосіб знаходження площі рівнобедреного трикутника.

Гострі й нескінченні дискусії про їх призначення ведуться з часів Геродота. Грецький філософ Прокл Діадох (бл.410-485) вважав піраміду Хеопса «свого роду кам’яним підручником астрономії і геометрії та знань, які пов’язані з розливами Нілу. Весь цей досвід закріплювався в розміщенні, обрисах, написах піраміди». Чого тільки не знаходили у великій піраміді: число π і золотий поділ, числові характеристики Землі й Сонячної системи, навіть пророкування про кінець світу 1920 або 1922, 1936 років і так далі.

Піраміди — незаперечний доказ великого запасу математичних знань, якими володіли древні геометри — перші зодчі. Це вони керували будівельними роботами, креслили плани і виконували всі необхідні обчислення.

V. Вивчення нового матеріалу

План вивчення теми:

1. Коли два відрізки рівні?

Якщо до точок А і В прикласти лінійку і провести лінію, то одержимо відрізок АВ. Той самий відрізок можна позначити ВА. Точки А і В називають кінцями відрізка.      

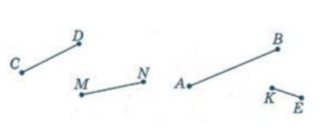Будь-які дві точки можна з'єднати лише одним відрізком. Довжину відрізка АВ також називають відстанню між точками А і В. Якщо два відрізки СD і МN мають однакову довжину, то відрізки рівні. Це записують СD = МN. Якщо довжина відрізка АВ більша від довжини відрізка KЕ, це записують так: АВ > KЕ або KЕ < АВ.

 

 

 

 

2. Коли два кута рівні?

Два кути називаються рівними, якщо при накладанні вони збігаються. Якщо сторони кутів утворені відрізками, то при рівності кутів рівність сторін може не зберігатися.

Учні пригадують які види кутів вони вже вивчили.

Приклади:

• Розгорнутим кутом називається кут, одна сторона якого є продовженням іншої.
• Два кути, що мають спільну вершину і спільну сторону, називаються прилеглими, якщо їх внутрішні області не покривають одна одну.
• Суміжними кутами називаються два прилеглих кути, у яких сторони, які не збігаються, утворюють пряму лінію.
• Щоб побудувати кут, суміжний даному, треба одну з сторін даного кута продовжити за його вершину.
• Вертикальні кути — такі два кути, у яких сторони одного є продовженням сторін другого і вони є рівними. Вертикальні кути утворюються при перетині двох прямих ліній.

3. Що робить токар або кравчиня, коли їм треба перевірити рівність двох деталей?

Учні разом з вчителем обговорюють проблему яка поставлена перед ними: «Що робить токар або кравчиня, коли їм треба перевірити рівність двох деталей?». Використовується метод «Мікрофон», по черзі діти висловлюють власні думки.

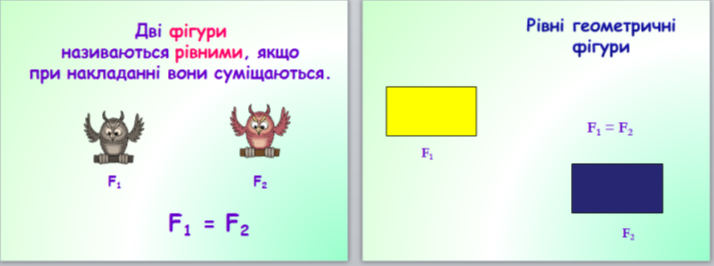
Означення: Дві геометричні фігури рівні, якщо ….

 

 

 

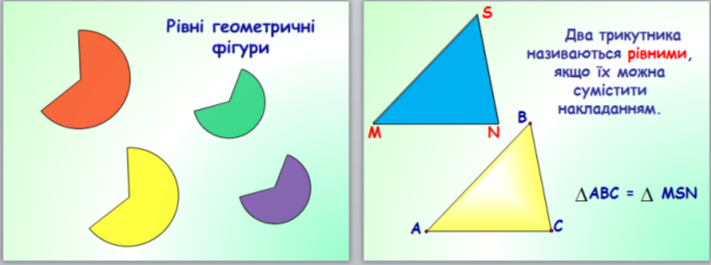
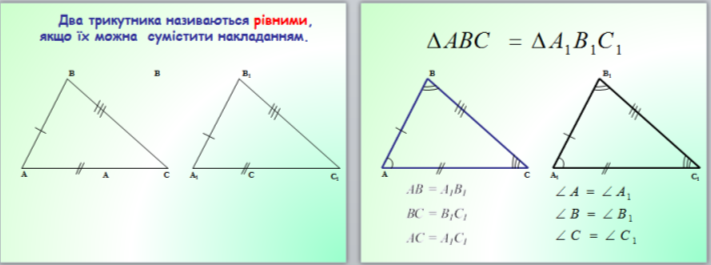
Означення: Два трикутника рівні, якщо ….

 

 

Два трикутники подібні, якщо кути одного трикутника відповідно дорівнюють кутам іншого трикутника та сторони одного пропорційні відповідним сторонам іншого.

 

6. Приклади.

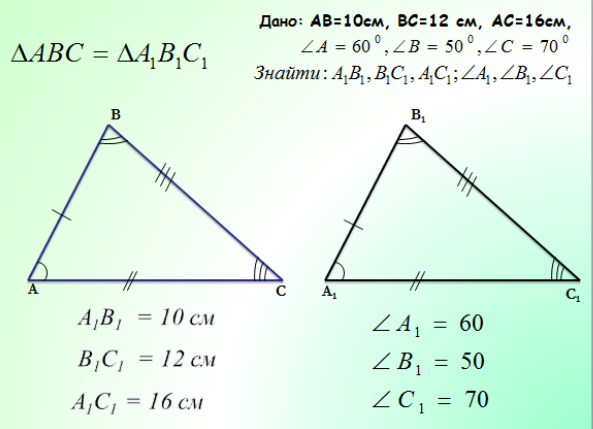
VI. Фізкультхвилинка.

VIІ. Первинне засвоєння нового матеріалу.

Робота в групах

Клас поділений на групи в яких групуються слабші учні з сильнішими. На розв’язання задачі виділяється 4-5 хвилин. Після цього лідери груп захищають свою думку стосовно рішення обраної задачі.

УСНО

1. Відомо, що ∆ PQE=∆ MNK. Заповніть пропуски:

PQ = ...; QE = ...; MK = ...;

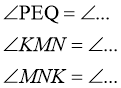
2. Відомо, що MP = DC; PT = CK; MT = DK;

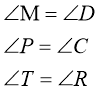         Назвіть рівні трикутники.

3. Що означає рівність ∆ ADC = ∆ PNK?

4. ∆ ABC = ∆ NKL. Відомо, що , ; .

Знайдіть інші кути даних трикутників

 

ПИСЬМОВО

 Задача № 1

Відомо, що ∆ABC=∆KLP; АВ = 5 CM; LP = 9 см; АС = 8 см. Знайти невідомі сторони трикутників ∆ ABC і ∆ KLP.

Розв'язання:

Оскільки ∆ABC=∆KLP, то

• AB = KL = 5 см;
• BC = LP = 9 см;
• АС = КР = 8 см.

Відповідь: 5 см; 9 см; 8 см.

Задача № 2.

Дано: ∆PKL= ∆KLP.

Знайти: РК.

Розв'язання:

За умовою ∆PKL = ∆KLP, звідси PK = KL; KL =LP; PL = KP.

Тоді всі три сторони ∆PKL рівні, а оскільки його периметр дорівнює 24см, то довжина однієї сторони 8 см. Тоді РК = 8 см.

Відповідь: 8 см.

VІIІ. Підсумок уроку.

Тестові завдання

І варіант

1. Якщо два трикутники рівні, то в них:

а) всі сторони рівні;

б) всі кути рівні;

в) відповідні сторони рівні та відповідні кути рівні;

г) навпроти рівних кутів лежать рівні сторони.

2. Два трикутники будуть рівні, якщо:

а) вони обидва рівнобедрені;

б) їх можна сумістити накладанням;

в) їх назви однакові;

г) вони обидва прямокутні.

3. ; АВ = 5 см, , , .

З цього випливає:

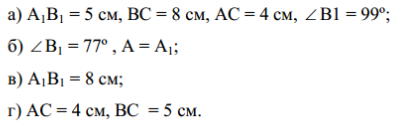
ІІ варіант

1. Якщо два трикутники рівні, то в них:

а) відповідні сторони рівні та відповідні кути рівні ;

б) навпроти рівних кутів лежать рівні сторони;

в) всі сторони рівні;

г) всі кути рівні.

2. Два трикутники будуть рівні, якщо:

а) вони обидва рівносторонні;

б) вони обидва тупокутні;

в) їх назви однакові;

г) їх можна сумістити накладанням .

3. ; DВ = 7 см, , , .

З цього випливає:

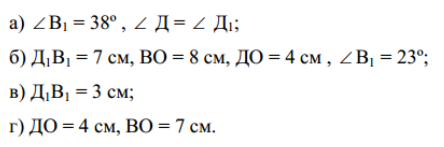
Кожен учень після виконання тестової роботи заповнює табличку та

порівнює свої результати з відповідями на дошці.

 

 

 

 

 

Історично-пізнавальна хвилинка.

 

 

VІІІ. Підсумок уроку.

Тестова робота

Учні отримують картки із завданнями для перевірки засвоєння

знань.

 

ІX. Домашнє завдання

Творче завдання: знайти приклади рівних фігур в архітектурних спорудах нашого міста.

Додатки