Урок " Розв'язування логарифмічних рівнянь"

Тема уроку: Розв’язування логарифмічних рівнянь.

Мета. Формування вмінь учнів розв’язувати логарифмічні рівняння різними методами : зведення логарифмічного рівняння до алгебраїчного ;  зведення логарифмів до однієї основи ; метод логарифмування;

Розвивати : уміння розв’язувати логарифмічні рівняння різними методами

та  зацікавленість до предмету

Виховувати математичну культуру мовлення, прищеплювати бажання мати глибокі знання

Обладнання: мультимедійне обладнання, роздатковий матеріал, інтерактивні завдання, розроблені в додатку learningapps

Хід уроку

І Організаційний етап.

Привітання учнів. Перевірка готовності до уроку учнів класу.

ІІ Перевірка домашнього завдання

Перевірити наявність та якість виконання домашнього завдання та відповісти на запитання учнів, які виникли під час його виконання.

ІІІ Повідомлення теми та мети уроку.

Вчитель:

- На попередньому уроці ми ввели поняття логарифмічного рівняння і розглянули деякі методи його розв’язання.

Сьогодні на уроці ми познайомимося ще з іншими методами розв’язування логарифмічних рівнянь, застосвуючи отримані знання на практиці.

ІV Актуалізація опорних знань

Вчитель:

-         При розв’язані логарифмічних рівнянь використовують  означення логарифма,властивості  логарифмічної функції та властивості логарифма

Почнемо наш урок з усної вправи «Заповніть пропуски»

1 Логарифмом числа b за      а називається       степеня,  до якого потрібно                     основу а, щоб отримати число b.

2 Число, яке стоїть під знаком логарифма, повинне  бути                 .

3 Функцію, задану формулою                   називають логарифмічною функцією з основою a.

4 Область визначення логарифмічної функції — множина всіх                    чисел

5  Множина значень логарифмічної функції — множина   всіх                 чисел.

6 Логарифмічним називають рівняння ,яке містять              під знаком логарифма  

7 Розв’язати логарифмічне рівняння означає знайти його                         або   переконатися, що їх взагалі                    

Вчитель:

-         Згадаємо властивості логарифма

 Learning Apps.org «Властивості логарифма»

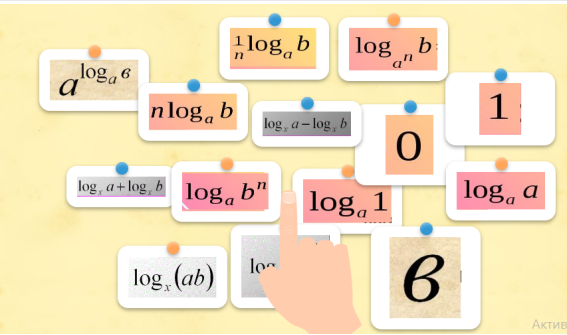
Вчитель:

-         Обчисливши логарифм, знайденому значенню поставте у відповідність букву і дізнайтеся прізвище та ім’я англійського математика, який вперше ввів поняття логарифма

= 3            о                                        = 4         Д

           = 4          н                                        =2         е

   = 2         п                                            = 3      ж

           = 0         р                               = -2     Н

 

   16                  - 64                8                          4

 

                   3                   100                     3                           2

 

  Історична хвилина (Повідомлення учня про Джона Непера)

Вчитель:

- Згадайте, якими методами ми навчилися розв’язувати логарифмічні рівняння

1.За означенням логарифма

2.Метод потенціювання та використання властивостей логарифма

3.Графічний

V Мотивація навчальної діяльності.

Вчитель:

-         Переходимо до розв’язання логарифмічних рівнянь іншими методами

Розв’язати рівняння:  - 7 + 2 = 0

-         Чи можна дане рівняння розв’язати одним із вже відомих нам методів? Що ви помітили?  Що ви пропонуєте зробити? 

VI Сприймання і усвідомлення нового матеріалу

Метод введення нової змінної

  - 7 + 2 = 0

 ОДЗ: х  ˃ 0,              Введемо заміну 

3 t² - 7 t + 2 = 0, D = 49 – 4 3 2 = 49 -24 = 25,  = 5,

t₁ = =  = 2, t₂=   =   =    1.

     2, х  = = 4,  є ОДЗ

     , х = , х = є ОДЗ

Відповідь: 4 ;

-         Оскільки після заміни змінної отримали алгебраїчне рівняння, то цей метод називають ще способом зведення логарифмічного рівняння до  алгебраїчного.

Робота в парах (ЗНО,2015 Завдання 30)

Розв’язати рівняння:

+ -2 = 0    ;     ( + ) = 3

Якщо рівняння має один корінь, то запишіть його у відповіді,

якщо рівняння має кілька коренів, то у відповіді запишіть їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100.

(розв’язок  рівнянь за закритою дошкою)

Перевірка розв’язаних рівнянь з розв’язанням на дошці

Метод зведення до однієї основи

Розв’язати рівняння:

- 2 = 3

ОДЗ: х ˃0,

перейдемо до логарифма із основою 3

- 2 = 3

+2 = 3, 3 =  3 = 1, х = 3 є ОДЗ

Відповідь: 3

Попрацюємо разом

Робота з підручником «Математика. Алгебра і геометрія. Рівень стандарт. Авт.Мерзляк) №6.4(2)

Один учень розв’язує  біля дошки

Розв’язати рівняння:

+  + = 11,

ОДЗ: х ˃0,

 Перейдемо до логарифма із основою 2.

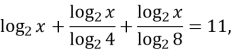
Відповідь: 64.

Метод логарифмування

Вчитель: Цей метод застосовують до рівнянь, якщо логарифм з невідомим знаходиться в показнику степеня.

Розв’язати рівняння:

= ,  

ОДЗ:

  = ,

  = - , 

= 2 -,

- – 2 = 0, заміна = t,  t² -  t - 2 = 0 , t₁+ t₂= 1, t₁t₂= - 2, t₁ = 2, t₂= -1.

= 2,  х = 10² = 100 є ОДЗ

= -1, х = = 0,1 є ОДЗ

Відповідь:0,1;100

Попрацюємо разом

Розв’язати рівняння:

=

Один учень розв’язує  біля дошки

ОДЗ:

          =, 

=  -3

  - 4 + 3 = 0

  Заміна = t, ,  t² - 4 t + 3 = 0 , t₁+ t₂= 4, t₁t₂= 3, t₁ = 3, t₂= 1.

= 1, х = 3, є ОДЗ

  = 3, х = 3³= 27 є ОДЗ

Відповідь:3;27

Перевіркою переконуємося, що корені рівняння 4 і

Отже, ми з вами розглянули  розв’язання  логарифмічних рівнянь ще декількома методами в залежності від виду рівняння.

Давайте ще раз пригадаємо методи розв’язування логарифмічних рівнянь

Поставте у відповідність логарифмічне рівняння й метод його розв’язання

+ =                                  За означенням логарифма

= 2                                             Зведення  до однієї й тієї ж основи                

=        Метод логарифмування

= 9                                                      Метод потенціювання

  - – 2 = 0                                    Графічний метод

 

     = х - 6                                                Алгебраїчний метод      

Польському математику Станіславу Ковалю належать такі слова: «Рівняння– це золотий ключ, який відкриває всі математичні сезами».

Сьогодні ми з вами відкрили один із математичних сезамів  – це логарифмічні рівняння та методи їх розв’язання

VIІ Підсумок уроку

-         Чи є універсальний метод розв’язування логарифмічного рівняння?

-         Який метод вам сподобався найбільше?

-         Як уникнути втрату коренів або появу зайвих коренів при розв’язуванні логарифмічних рівнянь?

-         Який метод виявився найскладнішим?

 

VIІІ Повідомлення домашнього завдання