Урок "Розв’язування прикладних задач. Самостійна робота."

О. М. Надточій,

 вчитель математики

 Будищенської загальноосвітньої

 школи І-ІІІ ступенів

Черкаської районної ради Черкаської області

Кваліфікаційна категорія «спеціаліст першої категорії»

Формування ключових компетентностей через навчальні математичні завдання на різних етапах уроку.

    Матеріал, запропонований у розробці уроку містить розширені методичні матеріали пізнавального характеру для використання вчителем при вивченні розділу « Відстань від точки до прямої» на всіх уроках та на кожному етапі уроку на розсуд вчителя. Для оптимізації подачі нового навчального матеріалу та зацікавлення учнів при вивченні  основних понять планіметрії та застосування знань до розв’язування прикладних задач через позитивні емоції -могутній стимул  здобуття знань, формуючи у школярів основи народної моралі та загальнолюдських цінностей.

Розділ 2. «Взаємне розташування прямих на площині.»

  Урок № 13. Тема. Розв’язування прикладних задач. Самостійна робота.

Серед рівних розумом – за однакових умов – переважає той, хто знає геометрію .

                                                                                    Б. Паскаль     (СЛАЙД 2)   

• Основна мета: формувати ставлення учнів до математики як невід’ємної складової загальної культури людини, необхідної умови її повноцінного життя в сучасному суспільстві; забезпечити оволодіння учнями математичною мовою, формувати  здатність пояснювати та доводити математичні твердження.
•  Освітня: відтворити в пам’яті учнів означення та властивості вертикальних  та суміжних  кутів, дослідити значення градусної міри кута між прямими, сформувати математичні компетенції : процедурну (уміння розв’язувати типові задачі), логічну (володіння індуктивним та дедуктивним методами), технологічну(володіння сучасними математичними пакетами), дослідницьку (володіння методами дослідження практичних та прикладних задач), методологічну (уміння оцінювати доцільність використання математичних методів для розв’язування практичних та прикладних задач).
• Розвивальна: узагальнити та систематизувати знання, уміння та навички, набуті учнями при вивченні тем: «Перпендикуляр. Відстань від точки до прямої. Кут між двома прямими, що перетинаються», розвивати варіативність та критичність мислення, здатність до аналізу та синтезу, вчити учнів складати прикладні задачі за готовими рисунками, формувати практичну та логічну компетенції шляхом розвитку  уміння   виконувати охайні побудови; відтворити в пам’яті учнів означення суміжних та вертикальних кутів, вчити обґрунтовувати та аргументувати гіпотези, застосовуючи раніше вивчені аксіоми, теореми, базові задачі та особистий досвід, розвивати  уміння працювати з підручником, шукати і використовувати додаткову навчальну інформацію, виокремлювати головне, формувати  здатності обґрунтовувати твердження, забезпечувати  оволодіння учнями мовою геометрії, розвивати  їх просторові  уявлення, розвивати уміння виконувати геометричні побудови за допомогою геометричних інструментів, привчати учнів застосовувати здобуті знання у навчальних і життєвих ситуаціях.
• Виховна: формувати  соціальні, комунікаційні  компетенції, застосовувати математичні методи у процесі розв’язування навчальних і практичних задач, розвивати уміння застосовувати здобуті знання у навчальних і життєвих ситуаціях; виховувати патріотизм, любов до праці, цікавість до вивчення геометрії, виховувати почуття власної гідності, привчати до виконання охайних рисунків.

Наочність і обладнання: набір демонстраційного креслярського приладдя.

 Очікувані результати:

Учень/учениця:

• наводить приклади перпендикулярних прямих, знаходить, показує та будує перпендикуляр з даної точки до даної прямої
• пояснює: що таке  перпендикуляр та не перпендикуляр
• формулює: означення: перпендикулярних прямих, перпендикуляра
• вимірює та обчислює відстань від точки до прямої
• зображує та знаходить на малюнках перпендикуляр; не перпендикуляр 
• застосовує вивчені означення і властивості до розв’язування задач
• наводить приклади перпендикулярних прямих, перпендикуляра, опущеного з даної точки до даної прямої;

Тип уроку:  Урок узагальнення та систематизації знань.

                    Хід уроку

1. Організаційний етап.

2. Перевірка домашнього завдання.

3. Актуалізація опорних знань

Виконання усних вправ

1. На рисунку 1 знайдіть пари суміжних кутів.

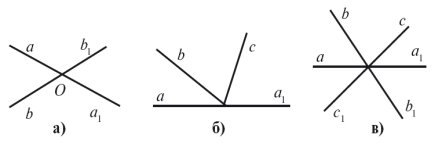
2. Що можна сказати про кут, суміжний з даним, якщо цей кут: а) прямий; б) тупий; в) гострий?

3. Дано пряму a та прямі b і c так, що Чи можуть прямі b і c перетинатись?

№ 7.1. Знайдіть градусні міри всіх кутів, які утворились при перетині двох прямих, якщо: а) всі кути рівні між собою (І в.);

 б)різниця двох з них 40˚ (ІІ в.);

 в) сума двох з них 140˚ (ІІІ в.);

г) два кути відносяться як 3:6 (І в.);

 д) сума  двох з них 60˚ (ІІ в.);

 е) три з них рівні між собою (ІІІ в.);

 є) сума трьох кутів дорівнює 280˚ (І в.);

 ж) один з утворених кутів у  два рази менший за другий (ІІ в.);

з) один з утворених кутів у  три рази більший за другий (ІІІ в.).

№ 7.2. Накресліть пряму, побудуйте точку, що не належить їй, знайдіть відстань від точки до прямої. Відповідь обґрунтуйте.

3. Мотивація навчальної діяльності учнів. (Загальнокультурна (комунікативна))

Геометрія – одна з найдавніших частин математики, яка вивчає просторове відношення і форми тіл. З геометрії зародилася  математика як наука. Люди з давніх-давен використовували геометричні знання в побуті. Геометричні форми були не тільки побутовими предметами, але й культурними. Геометрія – наука, яка дала людям можливість знаходити площі та об’єми, правильно креслити проекти будівель та машин. Таким чином, вона є основною частиною“фундаментом”, на якому будується не менш важливий напрямок діяльності людини – архітектура. Архітектура – це з’єднання мистецтва, науки та виробництва.

Архітектуру часто називають дочкою геометрії. Необхідність побудови прямокутника, знаходження його осей для встановлення ряду стовпчиків, визначення їх розмірів для створення матеріалу та інших незамінних в будівництві операцій потребують засвоєння відомих прийомів будівництва архітектурної форми. Практика інженерів, досвід, який передався в спадок, спонукали складання визначених правил, геометричних побудов.

Геометрія в архітектурі та мистецтві

        Уже в XII ст. архітектура вивчається як наука, як знання, як геометрія, яка має практичне значення, як діяльність, яка потребує не тільки великого досвіду, навиків і смаку, але й наукових знань. Архітектурна практика античної епохи, яка потребує від архітектора спеціальних математичних знань, викликала це уявлення. В погляді на архітектуру зіграло також важливу роль метафізичне трактування геометрії як основи всякої творчості, розповсюдженої у філософському і науковому світогляді XII ст. Його вплив і широке розповсюдження в інтелектуальному середовищі ХІІ ст. зобов’язане інтенсивному проникненню на Захід арабської філософії та науки, творів арабських математиків і перекладів грецьких робіт з геометрії. До них відноситься і метод геометричного доведення метафізичних положень, який широко використовують в середньовічній філософії. В філософії  Шартрської школи було віртуозно розроблене питання про принципи творення: про створення світу “мірою, числом, і вагою”. Звідси це велике значення, яке передавалось в роботах геометрії. Геометричні принципи розуміються в філософії Шартрської школи як основа всякої творчості - як Бога і природи, так і людини. Подібно тому як Бог в процесі творення починав з створення “багатьох тетраедрів, чи кубів, чи кіл, чи сфер, чим зберіг рівновагу в розмірах”,  так і людина прямує до пізнання від знань геометрії. “Існує чотири принципи, які ведуть людину до пізнання Творця, а саме – доказу арифметики і музики, і геометрії, і астрономії”, - писав  Шартрський. В першу чергу геометрія відображає стан художньої практики в епоху появи і наростання тенденцій до виробництва готичних конструкцій і нового архітектурного стилю.  В епоху зрілого середньовіччя архітектура розуміється, в дійсності, як прикладна геометрія. В деяких документах XII та ХІV ст. мистецтво геометрії трактується як синонім архітектури. В ряді документів ХІІ – ХІІІ ст., зв’язаних з будівельною практикою, з’являється термін “geometrici” – “геометри” для позначення архітекторів та будівельників воєнних укріплень. Дякуючи високому рівню знань готичних архітекторів були зведені величні та обширні готичні храми, в яких логіка пропорційного будівництва пронизувала всю багатогранність архітектурних елементів. “Мистецтво є наука”, “Мистецтво без науки нічого не варте”, - заключили в кінці ХІV ст. архітектори-консультанти з будівництва Міланського собору. Розуміння мистецтва як знання, як науки надзвичайно характерно для готичної епохи. Мистецтво цінувалось в той час як раціоналістична діяльність. Чим більше в ньому було від науки, чим більше воно опиралось в своїй практиці на точні знання, тим більш високе положення воно займало. Уявлення про мистецтво і науку в той час змінювалось, в ньому закладався різний сенс.

Геометрія в архітектурі Давньої Греції

Величними будівлями епохи Нового царства стали храми, або“будинки” богів. Один із них – заупокійний храм цариці Хатшепсут (1525 – 1503 рр. до н. е).

Жінка – фараон Хатшепсут була неабиякою особистістю. Захопивши владу у пасинка, майбутнього Тутмоса ІІІ, вона під час свого правління не стільки воювала, скільки відновлювала старі і будувала нові храми. З її ім’ям зв’язана також далека морська експедиція в країну Пунт. Тендітна та мініатюрна жінка з характерним контуром вузького лиця, високим чолом і широко розставленими очима завжди зображалась в чоловічому вигляді: з накладною борідкою. Така була тенденція зображення фараонів. Хатшепсут, бажаючи затвердити свою владу над підлеглими, які ще не привикли бачити жінку на троні, слідувала давно затвердженими правилами. Після смерті цариці Тутмос ІІІ знищив статуї  Хатшепсут, її ім’я в написах було збито. Храм в Дейр Ель– Бахрі побудував архітектор Сенмут, царський фаворит, наділений великою владою. Храм стоїть біля підніжжя стрімких скель Лівійського плоскогір’я, які не тільки служать неабияким фоном для архітектури, але й зливаються з нею в одне ціле. Храм знаходиться на трьох терасах, які з’єднані пандусами. Щоб відвідати храм, потрібно було пройти по алеї сфінксів, яка тяглася від берега Нілу, і піднятися по терасах до гробниці, вирубаній в скелі. Строгий вигляд храму урізноманітнили статуї цариці Хатшепсут у вигляді Осіріса; колони, на капітелях, на яких була висічена голова богині Хатор; розписи і розфарбовані рельєфи ( на багатьох з яких ображалась подорож в далеку країну Пунт). На просторих терасах розміщувались водойми, росли дерева. Зверніть увагу на чіткі прямокутні колони. Храм в Дейр Ель– Бахрі був побудований так добре і точно, що, не дивлячись на багато тисячоліть дойшов до нас в первинному вигляді. Якщо подивитися зверху, то ми побачимо 4 подібних прямокутників, це видно на малюнку.

Геометрія при будівництві метро

Метро ( франц. metropolitain, буквально – столичний, від грец.metropolis – головне місто, столиця), міська, не вулична залізна дорога для масових швидкісних перевезень пасажирів. Назва М. прийнято в СРСР і в багатьох інших країнах; інша назва –“підземка”. Метро –найпопулярніший вид транспорту в Києві.

Перший етап будівництва є створення креслення. Далі вимірюють довжину та висоту ескалатора. Це робиться просто – прикладають прямокутний трикутник, вимірюють катети (висоти і довжину викопаної ями) і за теоремою Піфагора – квадрат гіпотенузи дорівнює сумі квадратів катетів, шукаємо довжину ескалатора.

Розташовуючи ескалатор, використовують знання тригонометрії. В будівництві ескалатора приймають участь математики, архітектори, електрики і дизайнери. Після ескалатора будують залізно дорожні шляхи, тут особливої геометрії не потрібно, тільки не змінювати відстань між краями.

Архітектура України: Церква Пресвятої Євхаристії  (Львів)

У 1749 році за проектом інженера і архітектора Яна де Вітте був закладений фундамент костелу. Будівництвом керував Мартин Урбанік, з 1764 року — Христофор Мурадович, а закінчував фасад Себастьян Фесінґер. До 1764 року будівництво було, в основному, завершене, але після пожеж 1766 і 1778 років роботи відновилися. У 1865 році за проектом архітектора Юліана Захарієвича до костелу прибудували чотириярусну дзвіницю. А 1895-го був перебудований ліхтар на куполі, у 1905—1914 роках — відреставрований інтер'єр. Згодом, вже у радянські часи, храм відновлювали у 1956—1958 роках.

Костел споруджений у стилі пізнього бароко за західноєвропейским зразком. Кам'яний, в плані він зображає витягнутий хрест з овальною центральною частиною і двома дзвіницями по боках. Звеличує церкву величезний еліптичний купол. Масивні здвоєні колони підтримують галереї і ложі, прикрашені дерев'яними статуями роботи львівських скульпторів другої половни ХVІІІстоліття. Над галереями — колони барабана, що підтримують купол. Під банею костелу — цитата латинською мовою з Першого послання Тимофію: «Soli Deo honor et gloria» («Єдиному Богу честь і хвала»).

В інтер'єрі храму збереглися скульптури Себастьяна Фесінґера.

Собор Святої Софії (Київ)       

Київський Софійський собор був однією з найбільших будівель свого часу. Загальна ширина храму — 54,6 м, довжина — 41,7 м, висота до зеніту центральної бані — 28,6 м. Собор має п'ять колон, завершених на сході апсидами, увінчаний 13-ма верхами, що утворюють пірамідальний силует, і оточений з трьох боків двома рядами відкритих галерей, з яких внутрішній має два яруси. Довгий час вважалося, що галереї прибудовані до собору пізніше, але дослідженнями останнього часу доведено, що вони пов'язані з ним єдиним задумом і виникли водночас. Тільки хрестильня, вбудована у західну галерею, належить до середини XII ст.

Отже, ми переконалися у необхідності вивчення науки (геометрії), яка дає можливість глибше зрозуміти такий напрям в архітектурі, як давньоруське зодчество та розглянути значення геометричних законів і закономірностей в зодчестві, їх практичне застосування при проектуванні та побудові споруд. Джерелом для заповнення дефіциту знань та інформації виявилась література про золоту пропорцію.

Ми дізнались, що архітектура починається з геометрії. З найдавніших часів архітектори спиралися на математичні принципи. Стародавній римський архітектор Вітрувій Маркус вважав, що будівельники завжди повинні використовувати точні співвідношення при будівництві храмів. Без симетрії і пропорції храм не може мати регулярний план. З цього твердження ми бачимо, що в архітектурі головне місце займає симетрія та золота пропорція.

В науковій літературі з дослідження пам’ятників архітектури виявлені зразки гармонічної єдності, найкращі витвори  людського генія: храм Дейр Ель – Бахрі, Церква Пресвятої Євхаристії у Львові, собор Святої Софії в Києві, собор Василя Блаженного в Москві, Архангельський собор в Москві, церкви Надвірнянщини, Манявський скит та Пнівський замок.

Ми також довели, що трикутник є однією з найпоширеніших геометричних фігур, у багатьох технічних виробах використовуються трикутні деталі або їх частини. Порівняння двох трикутників часто є елементом порівняння двох складніших геометричних фігур.

Ми почерпнули для себе багато нового та цікавого, зрозуміли важливість геометрії в архітектурі і мистецтві

Також у будівництві, архітектурі, ландшафтному дизайні, проектуванні застосовуються геометричні знання. Людям, які прагнуть бути успішними, слід добре знати геометрію та вміти застосовувати вміння на практиці.    

4. Повідомлення теми, мети та завдань уроку.

Сьогодні на уроці ми розв’язуватимемо задачі прикладного характеру, застосовуючи раніше засвоєний обсяг знань та ваш власний  досвід.

5. Узагальнення окремих фактів, подій і явищ. (Загальнокультурна (комунікативна))

Учні об’єднуються в групи. (Прийом кластер.  Кластер – це спосіб графічної організації матеріалу, що дозволяє зробити наочними ті розумові процеси, які відбуваються при зануренні в ту чи іншу тему. Іноді такий спосіб називають «наочним мозковим штурмом».

 Послідовність дій проста і логічна:

1. Посередині чистого аркуша написати ключове слово, яке є «серцем» ідеї, теми.

2. Навколо «накидати» слова або пропозиції, що виражають ідеї, факти, образи відповідні для даної теми. (Модель «планета її супутники»).

3. Слова, що з’явилися, з’єднуються  прямими лініями з ключовим поняттям. У кожного з «супутників» у свою чергу теж з’являються «супутники», встановлюються нові логічні зв’язки.

У підсумку виходить структура, яка графічно відображає наші роздуми, визначає інформаційне поле даної теми.

У роботі над кластерами необхідно дотримуватись таких правил

Не боятися записувати все, що приходить у голову. Дати волю уяві та інтуїції. Продовжувати роботу, поки не скінчиться час або ідеї не вичерпаються. Постаратися побудувати якомога більше зв’язків. Не слідувати за заздалегідь визначеним планом.)

Повторюємо:

 а) означення перпендикуляра, основи перпендикуляра, перпендикулярних прямих;

б) як знайти кут між двома прямими, що перетинаються;

 в) як знайти відстань від точки до прямої;

 г) які задачі називаємо прикладними?

Робота за підручником.

 За рисунком до задачі №183 складіть задачу на знаходження відстані від точки до прямої.

6. Повторення і узагальнення понять та засвоєння відповідної системи знань. (Загальнокультурна (комунікативна))

Прослухаємо Гімн України:

«Ще не вмерла України ні слава, ні воля.

Ще нам, браття колодії, усміхнеться доля.

Згинуть  наші воріженьки як роса на сонці.

Запануєм і ми, браття, у своїй сторонці…».

 Обчислюють кількість приголосних у четвертому рядку  ті учні, хто працює на І варіанті. На дошці записані слова: «Справедливі  семикласники».  Кількість приголосних підраховують  ті учні, хто працює на ІІ варіанті.  Знаходять різницю. В результаті отримуємо 2. (Інформаційна)

№ 7.3. Побудуйте дві точки. Проведіть пряму l. Зобразіть точку M, яка не належить даній прямій.

№ 7.4. Проведіть пряму MN, що перпендикулярна до прямої l.

Завдання для команди «Сміливі»

№7.5. Знайдіть відстань від точки М до прямої l.

№ 7.6. Зробіть висновок.

Завдання для команди «Спритні»

№ 7.5. Знайдіть довжину МК.

№ 7.6. Порівняйте МК і MN.

№ 7.7. Зробіть висновок.

Завдання для команди «Сильні»

№ 7.5. Позначте точку О – точку перетину прямих МК і MN.

№ 7.6. Знайдіть величину кута між прямими МК і MN.

№ 7.7. Зробіть висновок.

7. Повторення і систематизація основних теоретичних положень  і провідних ідей при розв’язуванні прикладних задач

№ 7.8. Висота «гірки» на дитячому майданчику  2 метри. Побудуйте ескіз «гірки» для дітей молодшого та старшого дошкільного віку (автономні спуски) у масштабі 1:100.

(Здоров’язберігаюча)

№ 7.9. Глибина басейну 3 метри. Накресліть ескіз східців до басейну. (Здоров’язберігаюча)

№ 7.10. Відстані від школи до будинків Тараса, Максима та Богдана відповідно дорівнюють 600м, 700м та 200м. Побудуйте план. (Інформаційна)

№ 7.11. Довжини паперових гірлянд, які виготовили Іванна, Дарина та Софія, відповідно дорівнюють 2м, 3м і 4м. Гірлянди прикріпили до верхівки ялинки.  Накресліть схему .   (Загальнокультурна (комунікативна))

 Домашнє завдання.

У результаті перетину двох прямих утворились 4 кути, кожен з яких менший від розгорнутого. Знайдіть градусну міру кожного кута, якщо:

          а) сума двох кутів дорівнює 78°;

          б) різниця двох кутів дорівнює 42°;

          в) один з кутів у 5 разів менший від іншого;

          г) один з кутів у 2 рази менший від суми двох інших;

          д) сума трьох кутів дорівнює 300°;

          е) сума трьох кутів більша від четвертого на 100°.

8. Підсумок уроку. (Загальнокультурна (комунікативна))

Інтерактивна гра. Продовжте речення:

1. Особисто для мене незвичним на уроці було…
2. Зацікавило мене…
3. Сподобалось …
4. Я навчився (навчилася)…
5. Тепер я вмію…
6. Мені запам’яталось…

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ                                                                                                                         

1.                     Концепція Нової української школи [Електронний ресурс]. - Режим доступу: http://mon.gov.ua/Новини%202016/12/05/konczepcziya.pdf
2.                     Майбутнє шкільної математичної освіти [Електронний ресурс]. - Режим доступу: https://www.pedrada.com.ua/article/1321-maybutn-shklno-matematichno-osvti

3. Оновлення програм для базової загальної середньої школи [Електронний ресурс]. – Режим доступу: https://www.ed-era.com/mon59/
4. Компетентність [Електронний ресурс]. - Режим доступу: https://uk.wikipedia.org/wiki/Компетентність
5. Забезпечення математичної компетентності випускниках вимога часу [Електронний ресурс]. – Режим доступу: http://oipopp.ed-sp.net/public/pg_magazine/pdf/pv_3_2017.pdf
6. [Електронний ресурс]. – Режим доступу:  proekt-geometriy.blogspot.com/p/blog-page.html
7. 0_8841d_53dad8da_XL.jpg
8. 4. Jpg
9. Node-5711-obs-dom. Jpg
10. 1.http://yandex.ua/images/