Урок з алгебри для учнів 11 класу на тему: "Тригонометричні рівняння з параметром"

Тема уроку:  Тригонометричні рівняння з параметром

Мета уроку: 

навчальна: Ознайомити учнів з основними методами розв’язування тригонометричних рівнянь з параметром,  сформувати в учнів здатність до застосування цих методів при  розв’язуванні тригонометричних рівнянь з параметром.  Навчити застосовувати набуті знання при розв’язуванні тригонометричних рівнянь різного рівня складності.

розвивальна: розвивати уміння аналізувати, висувати гіпотези, логічне та критичне мислення, увагу.

виховна: виховувати інтерес до вивчення тригонометрії, культуру математичної мови та письма, уміння працювати в колективі, наполегливість у досягненні мети.

Тип уроку: урок засвоєння нових знань та вмінь.

Обладнання: мультимедійний проектор, комп’ютер.

Хід уроку.

I. Організаційний етап.

Форма роботи: фронтальна. Метод: словесний.

Створення позитивного настрою учнів.

II. Формування мети й завдань уроку.

Форма роботи: фронтальна. Метод: словесний.

Доброго дня шановні учні та гості, що присутні сьогодні у нас на уроці! Сьогодні на уроці, ми ознайомимося з деякими методами розв’язування тригонометричних рівнянь з параметром та навчимося застосовувати набуті знання при розв’язуванні тригонометричних рівнянь з параметром різного рівня складності.

•             Повідомлення учням теми уроку. Діти, відповідно до теми уроку, які ваші очікування, чому ми

сьогодні повинні навчитися, які емоції повинні отримати? (хмаринка слів).

https://wordart.com/9eb08t3k0ih4/%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80

Бажаю всім успіхів у вивченні цієї теми!

III. Мотивація учбової діяльності учнів на уроці.

Форма роботи: фронтальна. Метод: словесний.

 Оцінювання на сьогоднішньому уроці ми проведемо використовуючи аркуш накопичення оцінок, який лежить у кожного на парті. Запишіть до нього своє прізвище та ім’я. Правильна відповідь на усне питання оцінюється 1 балом.

●  «Ніколи не зупиняйтесь на досягнутому! На шляху до своєї мети головне пройти всі перешкоди! Чим більше перешкод, тим вище самооцінка та рівень вашого успіху».

IV.  Актуалізація опорних знань учнів.

• Розв’язування тестових завдань: (максимальна кількість балів – 6)

1)     Знайдіть значення виразу sin

А	Б	В	Г	Д

2)      Знайдіть значення виразу соs

А	Б	В	Г	Д

 

3)       Укажіть властивість функції у = sinх

А	Б	В	Г	Д
D (у) = [-1;1]	Е (у) = (-∞; +∞)	Функція є спадною на D(у)	Функція є непарною	Функція є зростаю чою на D(у)

 

4)        Розв’яжіть рівняння  8 sinх = 7.

 

5)  Розв’яжіть нерівність

А	Б	В	Г	Д
[-1;3]	[-3;1]	(-1;4)	[-2;4]	(-3;1)

 

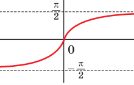
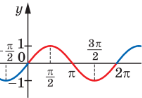
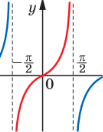
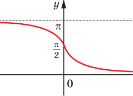
6)  Укажіть рисунок, на якому може бути зображений фрагмент графіка функції у = sinх

А	Б	В	Г	Д

 

Відповіді: 1Г;  2В;  3Г;  4А;  5Б;  6Б.

• Виконання інтерактивних вправ:

https://learningapps.org/watch?v=phsu58gxj20

V. Вивчення нового матеріалу.

Форма роботи: фронтальна, індивідуальна. Метод: проблемно-пошуковий.

Розв’язування біля дошки: 

№ 1. (ЗНО – 2011)  Знайдіть найменше значення параметра а, при якому має розв’язки рівняння

.

Розв’язання (аналітичний метод): 

Розглянемо ліву частину даного рівняння:

Шукані значення параметра а – це розв’язки нерівності: , яка рівносильна системі:

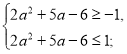
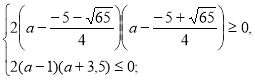
Відповідь № 1. При 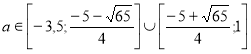рівняння має розв’язки.

Найменше значення а = -3,5.

№ 2. Визначте кількість коренів рівняння sinx = а на проміжку залежно від  параметра а.

Розв’язання  (графічний метод):  

Зобразимо графік функції  у = sinx  на вказаному проміжку  .         Кількість коренів визначається кількістю точок перетину горизонтальної прямої у = а з виділеною частиною графіка функції у = sinx. Точка не належить виділеній кривій, а точка 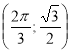- належить.

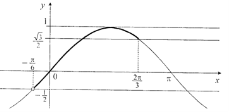
Будемо переміщувати горизонтальну пряму у = а знизу вгору, спостерігаючи такий результат:

1) Якщо  , то коренів немає;

2) Якщо   , то рівняння має один корінь;

3) Якщо   , то рівняння має два корені;

4) Якщо а = 1, то рівняння має один корінь;

5) Якщо а > 1, то коренів немає.

Відповідь: 1) Якщо  або а > 1, то коренів немає;

2) Якщо або  а = 1, то рівняння має один корінь;

3) Якщо , то рівняння має два корені.

• Рухавка: фізкультхвилинка для покращення мозкового кровообігу.

VII. Формування умінь та навичок учнів.

Форма роботи: фронтальна, індивідуальна. Метод: проблемно-пошуковий.

Користуючись вивченими методами проведемо подальшу роботу  в групах (по 8 учнів). Кожна група має консультанта, який керує роботою в групі. Завдання у груп різні: на 3 бали, на 4 бали та на 5 балів.

• Завдання групи середнього рівня навчальних досягнень учнів ( 4 - 6 балів):   № 1.

№ 1. (3б) Визначте, при яких значеннях параметра а рівняння

sin²x + (2a + 6) sinx + (2a - 7)(1 - 4a) =0 має розв’язки.

Розв’язання. Розглянемо дане рівняння як квадратне відносно sinх. D₁=(3а - 4)² Тоді отримаємо сукупність рівносильну даному рівнянню:

Шукані значення параметра а – це розв’язки сукупності: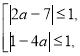

Відповідь: а є [0;0,5] або [3;4].

• Завдання групи достатнього рівня навчальних досягнень учнів ( 7 -  9 балів):  № 2.

№ 2. (4б) Визначте кількість коренів рівняння соs x = а на проміжку залежно від  параметра а.

 

 Розв’язання.   Зобразимо графік функції  у = cosx  на вказаному проміжку . Кількість коренів визначається кількістю точок перетину горизонтальної прямої у = а з виділеною частиною графіка функції у = cosx.

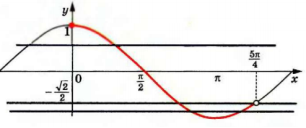
Точка (0;1) належить виділеній кривій, а точка 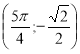- не належить.

Будемо переміщувати горизонтальну пряму у = а, спостерігаючи такий результат:

1) Якщо  , то коренів немає;

2) Якщо а = -1, то один корінь;

3) Якщо   , то рівняння має два корені;

4) Якщо   , то рівняння має один корінь;

5) Якщо а > 1, то рівняння коренів немає.

 

Відповідь: 1) Якщо  або  а > 1, то коренів немає;

2) Якщо а = -1 або, то один корінь;

3) Якщо   , то рівняння має два корені.

 

• Завдання групи високого рівня навчальних досягнень учнів (10 - 11 балів): № 3.

№ 3. (5б) Визначте, при яких значеннях параметра а, рівняння  sin²x - 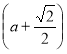sinx + = 0

має на проміжку :   1) два корені;  2) три корені.

Розв’язання. Розглянемо дане рівняння як квадратне відносно sinх. D =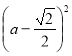

Тоді отримаємо сукупність рівносильну даному рівнянню: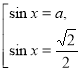

Обчислимо: sin 0 = 0,  sin=

Зобразимо графік функції  у = sinx  на вказаному проміжку . Друге рівняння сукупності на проміжку має два корені, тому для задачі № 1 треба, щоб рівняння  sinx = а не давало нових коренів або не мало коренів на проміжку, що розглядається.

При корені рівнянь сукупності збігаються;

При або а > 1 рівняння sinx = а не має коренів на проміжку .

Відповідь № 1. При або або а > 1 рівняння має два корені.

Для задачі № 2  треба, щоб рівняння sinx = а мало лише один корінь на проміжку, що розглядається:

а = 1 або

Відповідь № 2. При або а = 1 рівняння має три корені.

      Учні самостійно перевіряють виконану роботу, звіряючись з еталоном, виправляють помилки.

VIІI. Підсумок уроку.

Форма роботи: фронтальна. Метод: словесний.

Підведемо підсумок уроку, підрахуйте загальну кількість балів, отриманих за урок.

Картка самоконтролю Прізвище __________________________
1	1 завдання (тести)	6 балів
2	2 завдання (робота в групах)	3 або 4 або 5 балів
3	Усні відповіді	по 1 балу
	Всього (балів)

Оголошення оцінок, які отримали учні. В залежності від того, який результат отримав кожен учень:

IX. Повідомлення домашнього завдання.

Форма роботи: фронтальна. Метод: словесний.

 Домашнє завдання:

№ 1 (середній рівень) При яких значеннях параметра а має розв’язки рівняння:

sin²x - sinx + а(2а + 1) = 0.

№ 2 (достатній рівень) Визначте кількість коренів рівняння sin x = а на

проміжку залежно від  параметра а.

№ 3 (високий рівень) Визначте, при яких значеннях параметра а рівняння 

sin²x - sinx + = 0

має на проміжку : 1) один корінь;  2) два корені.

X.  Рефлексія діяльності.

Форма роботи: фронтальна. Метод: словесний.

Бесіда:

 – З якими методами розв’язування тригонометричних рівнянь з параметром ми сьогодні познайомилися?

– З якими утрудненнями ці методи допоможуть вам справитися?