Урок "Розвязування вправ з теми "Ділення раціональних чисел"

Тема. Ділення раціональних чисел

Мета: закріпити знання та відпрацювати навички використання правил ділення раціональних чисел окремо та разом з іншими правила­ми арифметичних дій над раціональними числами.

Тип уроку: застосування знань, умінь та навичок.

Хід уроку

І. Перевірка домашнього завдання

1. Знайдіть частку:

а) 3,6 : (-4); б) - 2,5 : (-7,5); в) - 8,64 : 1,2; г) - 56,68 :(-0,01);

2. На початку уроку можна дати математичний диктант.

Математичний диктант

Варіант 1 [2]

1. Виконайте ділення 1,8 на -2 [-2,4 на -4].
2. Чи можна обчислити частку 0 та (-5) [-8 та 0]?
3. Чи можна обчислити значення виразу -6 поділити на 0 [0 поділіти на -3]?
4. Розв'яжіть рівняння: -0,25х = 5[у : (-0,5) = -7]; с : (-2,3) = -2 [-0,34a = 0,68].

II. Актуалізація опорних знань

Під час перевірки правильності виконання математичного диктанту повторюють правила і деякі властивості ділення. Щоб повністю підготу­вати учнів до розв'язування вправ, запланованих на цей урок, розв'язуємо усні вправи.

III. Відпрацювання навичок

Усні вправи

1. Обчисліть частку:

2. Міні-гра «Повторимо»

3.Перевіримо правильність розв’язання.

а).  -3+(-5)=-8      б).-4-(-3)=1     в). -3∙5= 15   г).1-9=-8

4.Розв’язування вправ біля дошки.

4.1.а) (-28) : (-4) - 10; б) – 65 : 13 + 90 : (-15); в) (7 - 10) · (-18) + 42 : (-7);

г) 15 - (4 + 8 : (- 2)) - 6; д) 0,2 - : 11; є) -4 : - 10 : (-20).

4.2.Знайти  значення виразу 12 : х - 4,6, якщо: х = -3; -1,5; 4; -0,5.

4.3.Розв'яжіть рівняння:

a) -2x = 10; б) -3x = -9; в) 0,2x = -4; г) -1,2x = 3,6; д) -x = ; є) -х = -1

1. Додаткові вправа

 Знайдіть невідомий член пропорції:

а) ; б) ; в) ; г) .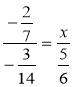

 Можна зауважити, що знак «·» у цих рівняннях (тобто значення виразу a·b:c, де a, b, c раціональні числа) так само залежить від кількості від'ємних чисел, як і знак добутку!

IV. Підсумки уроку. Мотивація оцінок.

Повторюємо правила і властивості ділення раціональних чисел.

V. Домашнє завдання

1. Обчисліть: а) -42 : 14 – 18 : (-2); б) -60 : 12 + (-2 - 8) · 5; в) -4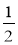: (-9).
2. Розв'яжіть рівняння: а) -3(3х + 1) = 15; б) 2 + 3(х – 3) = -13.