Урок-семінар по темі "Похідна"
Урок 14
Тема уроку. Урок-семінар по темі « Застосування похідної».
Мета уроку. Узагальнити та систематизувати практичні навички учнів застосування
вивченого матеріалу до розв’язування задач і вправ з даної теми; формувати вміння
переносити набуті знання у нові ситуації; розвивати інтерес до математики.
Обладнання: мультимедійна дошка, таблиці.
І. Організаційна частина.
ІІ. Перевірка домашнього завдання.
На дошці побудовано графік функції (черговий учень підготував малюнок на перерві), яку учні досліджували вдома:
У = -х4 + 2х2 + 3 (вправа 52 (5).
- D(у) = R.
- y( –x) = –( –x)4 + 2(–x)2 + 3 = –x4 + 2x2 + 3 = y(x).
Функція парна, графік симетричний відносно осі 0у.
- Нулі функції: у = 0; –х4 + 2х2 + 3 = 0; х4 – 2х2 – 3 = 0;
х2 = t; t2 – 2t – 3 = 0; t1 = –1, t2 = 3.
х2 = –1 – не має розв’язку;
x2 = 3, х = ![]() .
.
-
y' = –
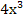 + 4х
+ 4х
y' = 0 –![]() + 4х = 0
+ 4х = 0
–![]() = 0
= 0
![]() ,
, ![]() – критичні точки
– критичні точки
5.Складаємо таблицю.
|
x |
|
-1 |
(-1;0) |
0 |
(0;1) |
1 |
(1; |
|
y' |
+ |
0 |
- |
0 |
+ |
0 |
- |
|
y |
|
4 |
|
3 |
|
4 |
|
|
|
|
max |
|
min |
|
max |
|
6.Будуємо графік функції.
Проводимо фронтальне опитування за малюнком.
- Парна чи непарна дана функція?
- Назвати проміжки зростання, спадання функції.
- Назвати точки екстремуму та екстремуми функції.
ІІІ. Мотивація навчання
Ми закінчуємо вивчати тему «Застосування похідної». Протягом вивчення теми навчились знаходити проміжки монотонності функції, точки екстремуму, найбільше та найменше значення, досліджувати функцію, будувати графіки.
На практиці людям часто доводиться розв’язувати задачі, де необхідно за допомогою найменших затрат сил, засобів і матеріалів одержати найкращий результат. Для розв’язування таких вправ ми застосовуємо похідну.
Повідомляємо тему і мету уроку.
Сьогодні на уроці ми працюємо під девізом : «Без ентузіазму - ніякої математики!».
ІV. Актуалізація опорних знань учнів.
- Сформулювати означення похідної функції у точці.
- Обчислити похідні (за допомогою проектора проектуємо на екран вправи):
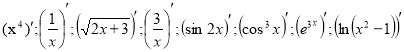
- Яка функція називається спадною (зростаючою) на проміжку?
- Яка точка називається критичною (стаціонарною) для функції у = ƒ(х)?
- Яка точка називається точкою максимуму (мінімуму) функції?
- Як визначити проміжки монотонності функції?
- Як дослідити функцію на екстремум?
- Як знайти найбільше та найменше значення функції на відрізку?
V. Розв’язування вправ.
Три учні одержують завдання, яке повинні виконати на дошці. Учні з класу теж розв’язують ці завдання: перша група – те саме, що перший учень, друга група – те, що другий учень, третя група – те, що третій учень.
Перший учень.
Вправа 47
15) Знайти інтервали зростання і спадання функції ![]()
Розв’язання
D(y) = R
y' = 4x3 – 4x.
Якщо y' > 0, то функція зростає, якщо y' < 0, то функція спадає.
Маємо :
4x3 – 4x > 0;
4x(х2 – 1) > 0;
х(х – 1)(х + 1) > 0.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
y' > 0 при х ![]() (–1;0)U(1;+∞) y’<0 при х
(–1;0)U(1;+∞) y’<0 при х![]() (-∞;-1)U(0;1)
(-∞;-1)U(0;1)
Другий учень.
Вправа 48
19) Знайти локальні екстремуми функції ![]()
Третій учень.
Вправа 50
8) Знайти найбільше і найменше значення функції ![]() на відрізку [-8;-1]
на відрізку [-8;-1]
З кожної групи один учень коментує розв’язання відповідної вправи, порівнюємо з результатами на дошці. Оцінюємо учнів, повторюємо алгоритм знаходження проміжків монотонності функції, екстремумів та найбільшого і найменшого значень на відрізку.
V. Творче завдання.
Щоб проілюструвати характерні властивості функції, можна звернутися до прислів’я. Адже прислів’я – це відображення стійких закономірностей, перевірених багатолітнім досвідом народу.
Тому, при підготовці до уроку, група учнів одержала творче завдання: підібрати такі прислів’я, які будуть характеризувати властивості функцій.
Будьте уважні, тому що ви повинні по змісту прислів’я назвати властивості функції, яка йому відповідає.
Прислів’я
1.Зростання, спадання функції.
Чим довше коріння, тим більше насіння.
Чим довше волосся, тим більше розуму.
Добре дбаєш, багато маєш.
Більше діла, менше слів.
2.Максимум, мінімум функції.
Порожній колос вище всіх стоїть.
Найбільша сила в світі – терпіння.
Найбільше каліцтво – ледачість.
VІІ. Дослідити функцію ![]() та побудувати її графік.
та побудувати її графік.
Повторюємо алгоритм дослідження функції.
Учень розв’язує вправу біля дошки з коментуванням, всі інші – в зошитах.
Розв’язання
- D(y) = R.
2. Функція ні парна, ні непарна.
3.![]()
4. – 6(х + 1)(х–3) = 0;
х1 = –1, х2 = 3 – критичні точки.
5. Нулі функції : (х–1) = 0; х = 1.
(1;0) – точка перетину з віссю 0х.
Якщо х = 0, то у = – 2 .
(0; –2) – точка перетину з віссю 0у.
6.Складаємо таблицю.
|
x |
|
-1 |
(-1;3) |
3 |
(3; |
|
y'(х) |
– |
0 |
+ |
0 |
- |
|
Y(х) |
|
–3 |
|
1 |
|
|
|
|
min |
|
max |
|
7.Будуємо графік функції.
Один з учнів класу підготував алгоритм дослідження функції у віршованій формі. Уважно слухаємо, таким чином, ще раз повторюємо алгоритм дослідження функції.
Загальна схема дослідження функції
Щоб графік будувати,
Треба дещо вміти й знати:
Алгоритм тримати просто,
Щоб усе пішло по росту.
Щоб успішно все розпочати,
треба область визначення знати
І правильно її написати.
А що ж далі нам робити?
Функцію на парність дослідити.
Знати треба усім гарно,
Чи парна, чи непарна,
Бо буває часом, що гарна,
а вона ні парна, ні непарна.
Ікс та ігрек нулеві прирівняти,
щоб якнайбільше точок на площині зібрати.
Крок наступний – похідна.
Її треба вміти добре шукати,
Щоб без помилок ƒ (х) узяти.
Щоб критична дочка правильна була,
Похідну прирівнюємо до нуля.
Заносимо в таблицю ми все акуратно.
По порядку розставляємо проміжки спочатку.
Знаками, значками, потім стрілочками.
Мінімум і максимум – все пишемо в таблицю,
Перетворюємо її в справжню чарівницю.
Далі на папері – біла білизна,
Вісь координат, а ще – площина.
На всій площині точки графічно зображаємо
І між собою плавно з’єднаємо.
Красива плавна лінія на графіку згинається,
Лиш оцінити працю вчителю лишається.
VІІІ. Усне розв’язування вправ.
- За допомогою проектора проектуємо на екран графіки функцій.
- На якому малюнку зображено графік:
а)швидкості руху тіла;
б)руху тіла;
в)прискорення руху тіла, якщо тіло рухається за законом s(t) = t3 + 1.
2. визначити, чи має дана функція точки екстремуму.
ІХ. Нестандартне застосування похідної.
Дуже часто ми зустрічаємось із практичними задачами , розв’язування яких зводиться до застосування похідної.
- Виступ учня, який підготував задачу з оповідання Л.М.Толстого.
Все життя селянин Пахом з оповідання Л.М. Толстого « Чи багато людині землі потрібно» мріяв мати якнайбільше землі. Одного разу доля звела його з купцем, який розповів йому про те, що їде від башкирців, в яких за тисячі рублів купив багато землі. Вирішив Пахом і собі поїхати.
Добравшись до башкирців і обдарувавши їх подарунками, попросив у них дозволу купити землю. Старійшина дозволив йому і сказав, що ціна у них – тисяча рублів за день. «Як це?» - питає селянин. «А так, - відповідають йому. – Скільки за день обійдеш – вся твоя буде. Тільки одна умова – щоб до заходу сонця прийшов на те місце, з якого вийшов».
Погодився Пахом, і з самого ранку виїхав у степ. Бажання захопити побільше землі було дуже великим.
На таблиці зображений шлях, який пройшов Пахом. Ми бачимо що йшов він по прямокутнику, периметр якого 40 км, S = 78 км2.
![]()
![]()

![]()
![]()
![]()
Прочитавши оповідання та зробивши деякі підрахунки, я зрозумів, що можна було б пройти той самий шлях, але площа була б більшою. Якби селянин йшов по квадрату із стороною 10 км, то S = 100 км2.
( х км – одна сторона, ( 20 – х) – друга сторона.
S = x(20 – x) = 20x – x2;
S'(x) = 20 – 2x.
S'(x) = 0, якщо 20 – 2x = 0, х = 10).
2.Виступ учениці, яка підготувала задачу Дідони.
Задача Дідони
За легендою, засновниця міста Карфаген Дідона, дочка тірського царя, посварившись з братом Пігмаліоном, втекла від свого батька і після багатьох пригод дісталась південного берега Середземного моря.
Тут у царя Уарбаса за деяку суму грошей вона купила ділянку землі, « Не більшу, ніж можна відміряти шкірою бика». Місцеві жителі неохоче дозволили їй зайняти навіть таку територію і розрахували ( розуміючи умову буквально) , що Дідоні для нового поселення дістанеться занадто мала ділянка.
Проте, винахідлива Дідона розрізала шкіру бика на тонкі смужки, зв’язала їх у ремінь і, закріпивши один його кінець на березі моря, пішла з другим кінцем у глиб країни. Тоді саме і постала перед нею задача: якої форми треба надати ременю, щоб «виміряти шкірою бика» якомога більшу площу.
Оточивши досить значну територію, Дідона заснувала на ній місто Карфаген. Легенда датує цю подію 825 роком до н.е.
Дідона зіткнулася із цікавою математичною задачею, яку часто називають її іменем. Серед усіх плоских фігур з периметром 1 ( 1 – довжина ременя) знайти ту, яка має найбільшу площу. Задача Дідони належить до так званих ізопериметричних задач.
До них, зокрема, належить і задача про знаходження замкненої кривої даної довжини, що обмежувала б найбільшу площу. Виявляється, що такою кривою буде коло. Дідоні для розв’язання задачі треба було обійти півколо з центром на березі моря. Довжина такого півкола повинна дорівнювати довжині зробленого нею ременя.
X. Тестовий контроль. За допомогою проектора на мультимедійну дошку проектуються диференційовані завдання на знаходження похідної.
ХІ. Підсумок уроку. Домашнє завдання
Вправа 48 (4;5) – І рівень; 50 (7) –ІІ рівень
Зошити збираємо для перевірки.


про публікацію авторської розробки
Додати розробку
