Урок "Способи задання функцій. Графік функції. Монотонність, парність і непарність функцій" №2

Тема заняття: Способи задання функцій. Графік функції. Монотонність, парність і непарність функцій.

Мета заняття: повторити основні способи задання функцій, пригадати графіки основних функцій. Поглибити знання студентів, ввівши поняття парної і непарної функції. Удосконалювати вміння досліджувати функції на монотонність аналітично і користуючись графіками.

Тип заняття: лекція комплексного характеру.

Обладнання: підручники, опорні конспекти, презентація «Парні  і непарні функції»

Література:

1. Алгебра і початки  аналізу: підруч. для 10 кл. загальноосвіт. навч. закладів М.І. Шкіль, З.І. Слєпканеь, О.С. Дубинчук.-К.: Зодіак – ЕКО, 2007. – 272 с.

2. Математика: Підручник О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов,  А.К.Сліпченко – К.: Вища школа, 2001.-447 с.

3. Чекова А.М. Алгебра. 7-12 класи: Навчальний посібник – 5-те видавництво.-Х.: Країна лерій. 2007.-120 с.

План заняття

I. Організація  початку  заняття.

ІI. Актуалізація  опорних  знань:

• Усне опитування студентів;
• Виконання усних вправ;
• Перевірка виконання домашнього завдання.

ІІI. Вивчення нового матеріалу:

1. Способи задання функцій.
2. Графік функцій.
3. Алгоритм дослідження функції на монотонність.
4. Алгоритм дослідження функції на парність і непарність.

IV. Виконання вправ.

VI. Підведення підсумків заняття.

VII. Домашнє завдання.

Хід заняття

I. Організація початку заняття.

ІI. Актуалізація опорних знань:

1. Питання до усного опитування:

- Що таке функція? Як позначають функції?

- Що таке аргумент функції, область визначення функції?

2. Виконання усних вправ:

• Знайдіть область визначення функції

а) ;   б)

• Як називається графік функції, заданої формулою:

а) ;   б) ;   в) y=3;     г)

3. Перевірка виконання домашнього завдання.

1)  2)

3)

ІІI. Вивчення нового матеріалу:

Основні способи задання функції

1. За допомогою формули 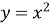(парабола); 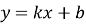(лінійна функція)
2. За допомогою таблиці
3. За допомогою графіка
4. Описово

Графіком функції називається множина точок

координатної площини, абсциси яких належать області визначення функції, а ординати є відповідним значенням цієї функції.

Зростання і спадання функції

Функцію називають зростаючою, якщо більшому значенню аргумента відповідає більше значення функції, тобто для будь-яких значень з області визначення функції таких, що , виконується нерівність і навпаки якщо зростаюча, то , виконується нерівність

Функцію називають спадною, якщо більшому значенню аргумента відповідає менше значення функції, тобто для будь-яких з області визначення функції таких, що , виконується нерівність , і навпаки: якщо – спадна, то за умови виконується нерівність .

Алгоритм дослідження функції на монотонність

Щоб дослідити функцію на монотонність, треба:

1) вибрати будь – які два значення і з області визначення функції такі, що ;

2) скласти різницю  і з’ясувати (якщо це можливо), чи буде вона додатною (від’ємною ) і, користуючись означенням числової нерівності, переконатися, що

Парність і непарність функції

Функція називається парною, якщо для будь-якого значення з області визначення значення також належить області визначення і супроводжується рівність . Графік парної функції семетричний відносно осі

Приклад 1: Чи парна функція

Д – функція парна

Приклад 2:

Д(, але –функція не парна

Функцію називають непарною, якщо для будь-якого значення із Дзначення – є Д і виконується рівність . Графік непарної функції симетричний відносно початку координат.

Наприклад: Чи непарна функція?

Оскільки Ді, функція не парна

Приклад:

Д, і , функція не є парною

Алгоритм дослідження функції на парність і непарність

Щоб дослідити функцію на парність і непарність, треба:

1) перевірити виконання умови : для будь – якого x з області визначення число (-х) також належить області визначення, тобто перевірити, чи є область визначення даної функції множиною, симетричною відносно початку відліку 0;

2) перевірити виконання умови: f(-x)=f(x)  чи   f(-x)=-f(x).

IV. Виконання вправ.

1. Побудувати графік функції і визначити, на якій множині значень аргументу дана функція спадає, а на якій зростає. При якому значенні х значення даної функції найменше.

• Розв’язання. Дана функція квадратична, її графік – парабола. Формулу

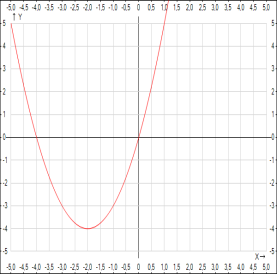
можна пожати в іншому вигляді: . З останньої формули видно, що значення функції дорівнюють нулю при x=0 і х= - 4.  У точках з такими координатами графік даної функції перетинає вісь х. Вісь параболи проходить через точку з абсцисою х=-2 . При такому значенні аргументу . За знайденими координатами трьох точок будуємо параболу. Як видно з графіка, дана функція спадає на проміжку (), зростає на проміжку (), а найменше значення має при

х=-2; воно дорівнює -4.

2. Парною чи непарною є функція:

а) ;  б) ;    в)

• Розв’язання.

а) Область визначення D (y) функції (множина всіх дійсних

чисел R)  є симетричною відносно 0 і . Отже, - функція парна.

б) , симетрична відносно 0 і

 . Отже, - функція непарна.

в) D(y)=R.

Отже,  функція   - ні парна, ні непарна.

Відповідь: а) парна;  б) непарна;  в) ні парна, ні непарна.

V. Підведення підсумків заняття.

1. Назвіть основні способи задання функцій.

2. які функції називаються парними? А які непарними? Наведіть приклади.

VI. Домашнє завдання.

Опрацювати §1 (п.1), № 2 (1 – 4 )