Розв'язування задач за допомогою пропорцій

Урок математики у 6 класі

Тема. Розв’язування задач за допомогою пропорцій

Мета: повторити означення та  основну властивість пропорції; формувати уміння і навички розв’язувати задачі за допомогою пропорції; знаходити невідомий член пропорції. Розвивати абстрактне мислення та творчі можливості учнів. Виховувати впевненість у необхідності математичних знань, активність, увагу, кмітливість. Прищеплювати любов до математики; показати учням можливості використання пропорції у різних галузях науки, мистецтва, повсякденному житті.

Тип уроку: вдосконалення знань, умінь і навичок.

Обладнання: презентація проекту «Як пропорції допомагають нам вивчати математику», мультимедійне обладнання для забезпечення технічної підтримки уроку.

Хід уроку

Недостатньо знати,

необхідно також застосовувати.

Анатоль Франс

1. Організаційний етап

Діти вітають присутніх на уроці. На екран спроектовано епіграф. Учитель про понує кільком учням висловити своє ставлення до слів французького письменника А. Франса  та схиляє їх до висновку, що знання не мають цінності, без можливості їх застосування на практиці.

У ч и т е л ь. Сьогодні на уроці ми проведемо дослідницьку роботу «Як пропорції допомагають  нам вивчати математику». У чому ж надзвичайна значимість і цінність пропорції?  У тому, що стосунки між людьми, життєві ситуації, які їх оточують у повсякденному житті, можна звести до розв’язання різних задач. А  для цього  необхідно навчитися їх розв’язувати.

2. Перевірка домашнього завдання

Учні заздалегіть об’єднані у три групи: історики, практики, публікатори.

Історики працювали над питанням використання пропорцій у давнину. Практики – «Для чого потрібні пропорції у повсякденному житі».  Публікатори допомогли учням класу оформити презентацію «Як пропорції допомагають нам вивчати математику», а також агітаційний буклет та бюлетень.

Бюлетень розмістили на стенді в графі «Сьогодні на уроці», буклети роздані присутнім на уроці гостям.

3. Актуалізація опорних знань

Учні з групи публікаторів демонструють слайдову презентацію «Як пропорції допомагають нам вивчати математику». «Історики» та «публікатори» коментують відповідні слайди. Потім всі розгадують кросворд «Пропорція»

1. Компонент дії віднімання
2. Члени пропорції a і d називаються…
3. Члени пропорції b і c називаються…
4. Як називається пропорція, значення лівої і правої частини якої є одне й те саме число?
5. Яким математичним терміном можна замінити слово «відношення»?
6. У правильній пропорції добуток крайніх членів дорівнює добутку середніх. Як називається ця властивість? 

4. Застосування знань, умінь та навичок

Учитель надає слово дослідникам практикам

У ч е н ь   п е р ш и й

У нас на черзі ще одна

Знань важлива порція:

Така рівність чарівна

На ім’я пропорція.

На уроках і в житті

Є завдань багато,

Де пропорції оті

Слід застосувати.

Щоб варити і пекти,

Майструвати, шити

Пропорційність величин

Треба добре вчити.

Є в пропорції властивість,

Допоможе нам вона,

Недарма така властивість

Мас назву «основна».

І пропорції — рівняння

Ти розв’яжеш без вагання,

Бо однакові в добутку

Члени в них –  середні й крайні.

Ф.В.Панішко

У ч и т е л ь. Діти, чи знадобляться нам в житті пропорці, які життєві завдання допомагають нам долати пропорції?

Пропорція – це ще один із чудових математичних інструментів, який допоможе кожному життєву ситуацію або ж задачу перетворити на красиве математичне речення.

У ч е н ь   д р у г и й. Пропорції допоможуть розв’язати задачі і на уроці, і вдома.

Задача 1. Ширина одного прямокутника 7 м, а довжина – 12 м. Знайти ширину другого прямокутника, якщо його довжина 14 м, а площі обох фігур однакові.

Розв’язання. Нехай м – ширина другого прямокутника. Тоді маємо відношення відповідних вимірів обох фігур

та .

Складемо пропорцію

.

Знайдемо невідомий член пропорції

;

м.

Відповідь: 6 м.

У ч е н ь   т р е т і й

Задача 2. Вінні Пух дуже полюбляє мед і за 5 днів з'їдає 1 кг меду. Скільки днів йому буде потрібно, щоб з'їсти 40 кг меду, який подарували йому на день народження? На скільки вистачить меду, якщо разом з Вінні Пухом їстимуть його друзі: П’ятачок, Кролик, Сова та Віслючок Іа?

Розв’язання. Нехай ведмедик з’їсть 40 кг меду за х днів. Як швидко Вінні Пух їсть мед можна судити з умови задачі: 1 кг меду за 5 днів або ж 40 кг меду за х днів. Маємо два відношення

та .

Складемо пропорцію

.

Знайдемо невідомий член пропорції

;

.

Якщо один із друзів з’їдає мед за 200 днів, то 5 друзів з’їдять за х днів.

Маємо пропорцію

.

Знайдемо невідомий член пропорції

;

.

Відповідь: за 200 днів з’їсть сам, за 40 днів – з друзями.

У ч е н ь   ч е т в е р т и й. Пропорції допомагають також розвязувати задачі на відсотки.

Задача 3. Майстерня Кота Базиліо «Оптика», що у місті Майстрів, виготовляє окуляри. У травні попит становив 65%. Скільки окулярів було продано у травні і скільки у квітні, якщо за два місяці кіт Базиліо продав 320 окулярів?

Розв’язання. Нехай у травні продано х окулярів це становить 65%, а разом продано 320 окулярів – 100%.

Маємо пропорцію

.

Знайдемо невідомий член пропорції

;

,

208 окулярів продано у травні,

320 – 208 = 112 окулярів продано у квітні.

Відповідь:208 і 112 окулярів.

У ч е н ь   п ’ я т и й. Пропорція є одним із основних інструментів розвязання задач в хімії та фізиці.

Задача 4. Гномик старанно доглядає за лісовими угіддями. Тому для виготовлення живильної замазки для дерев бере вапно, житнє борошно і олійний лак у відношенні 3:2:2. Скільки  Гномику потрібно взяти кожного матеріалу для виготовлення 8,4 кг замазки?

Розв’язання. Нехай х – одна із рівних частин матеріалу, тоді вапна у замазці три частини – тобто 3х, борошна – 2х, олійного лаку – 2х. Склавши всі пропорційні частини матимемо загальну масу замазки тобто: 3х+2х+2х=8,4кг; 7х=8,4кг; х=8,4кг:7; х=1,2кг;

3х=31,2кг=3,6(кг) вапна;

2х=21,2кг=2,4(кг) борошна;

2х=21,2кг=2,4(кг) олійного лаку.

Відповідь: 3,6 кг; 2,4 кг; 2,4 кг.

У ч е н ь   ш о с т и й. Пропорція також допомагає розв’язати задачу і на олімпіаді.

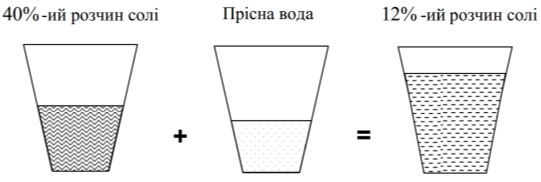
Задача 5. Скільки води треба добавити до 40-відсоткового розчину солі, щоб отримати 12-відсотковий.

Розв’язання.

Нехай x – маса солi (в грамах), яка мiститься у 600 грамах 40% розчину солi. Тодi має мiсце пропорцiя

.

Звідки

; .

Нехай далi y – загальна маса (у грамах) 12% розчину солi. Оскiльки в y грамах такого розчину мiститься точно 240 грамiв солi, то має мiсце пропорцiя

.

Звідси

; .

Для знаходження шуканої маси води (у грамах), яку необхiдно додати

до 600 грамiв 40% розчину солi, щоб отримати 12% розчин солi, необхiдно

обчислити рiзницю 2000 г – 600 г = 1400 г.

Вiдповiдь: 1 400 грамів.

У ч и т е л ь. І навіть завдання ЗНО після закінчення школи учням допоможе розвязати пропорція, яку ми вивчаємо у 6 класі.

Задача 6. (Завдання №27, ЗНО 2014) Відомо, що , де . У скільки разів число у більше за число х.

Розв’язання. Хочу зауважити, що на частину умови задачі «де » поки що не зважатимемо, її ми зможемо пояснити, коли пройдемо довгий, але цікавий шлях до 11 класу. Але відповідь на питання завдання зараз нам допоможе дати пропорція. Отже скористаємось основною її властивістю і перемножимо крайні і середні члени пропорції  .

Маємо

;

;

Будемо шукати невідомий у, який є зменшуваним:

;

.

З останньої рівності зважаючи, що її ліва та права частини є добутками крайніх та середніх членів пропорції, маємо рівність відношень

;

.

Відповідь: у більший за х у 2,5 рази.

5. Підсумки уроку

• Що нового дізналися на уроці?
• Чи цікаво вам було сьогодні на уроці?
• Чим запам’ятався урок?
• Чи задоволені ви своєю роботою?

6. Домашнє завдання

(згідно з підручником)

Додаткове домашнє завдання: скласти задачу, яку можна розв’язати за допомогою пропорції.