Урок. Тема: "Дроби та ноти"
Бінарний урок в 4 класі
з математики та музичного мистецтва
Тема: «Дроби та ноти»
Математика й музика потребують
єдиного мислення.
А.Енштейн
Шептуха Вероніка Андріївна
вчитель початкових класів
Янчук Алла Вікторівна
вчитель музичного мистецтва
Середня загальноосвітня школа №67
м. Києва
Мета: формувати:
ключові компетентності:
- уміння вчитися - організовувати робоче місце, вчитися самостійно здобувати знання з різних джерел, ділитися отриманими знаннями з однокласниками;
- громадянська – здатність екологічно мислити, бережливе ставлення до природних багатств, до людей; розвивати спостережливість, кмітливість, увагу, пам’ять, мислення;
- соціальна - продуктивно співпрацювати з різними партнерами в групі та команді, використовувати різні ролі й функції в колективі, проявляти ініціативу, підтримувати та керувати власними взаєминами з іншими;
предметні компетентності:
- повторити теоретичні знання про історію виникнення дробів, їх позначення, означення чисельника, знаменника та звичайних дробів;
- узагальнити отриманні знання про дроби на застосуванні їх в музиці, продовжуючи знайомство з нотами та їх довготою;
- систематизувати практичні навички додавання та віднімання дробів з однаковими знаменниками, обчислюючи музичний такт дитячих народних пісень.
- Навчити та поглиблювати знання учнів у музичній грамоті та розмірі, показати спільні паралелі в музиці на математиці;
- Розвивати музичні і творчі здібності учнів, почуття ритму;
- Розвивавати логічне мислення, правильне наукове мовлення, увагу, пам'ять, зосередженість, уважність, розумові здібності;
- Виховувати стійкий інтерес до шкільних предметів, розкриваючи зв`язок між ними; розширити словниковий запас учнів та компетентність про музичні твори та математичні дроби;
- Виховувати інтерес до чеської, польської, російської музики(до музики наших сусідів), музичний смак, красу.
Тип уроку: комбінований
Обладнання: ІКТ, презентація, картки для учнів, опорна схема «Дроби та ноти», музичний інструмент, ноти, портрети композиторів.
Музичний матеріал: Чеська народна пісня-танець «Полька», Фридерик Шопен «Вальс», Петро Чайковський «Марш», Алла Мігай «Сім нот», Оксана Перова-Рошки «Бо щастя – це…»
Хід уроку
І. Організаційний момент.
- Привітання
- Перевірка готовності до уроку
II. Мотивація навчальної діяльності
Гра «Синоптики» (жартівливий прогноз).
Прогноз погоди на урок.
Сьогодні у 4-Б класі на уроці музики та математики очікується безхмарне небо на уроці, сильний вітер від піднятих рук та глибоких знань, опади у вигляді високої кількості балів…
Упродовж найближчих 40 хвилин на вас очікує несподіваний град захоплюючих завдань про математику. На уроці ми почуємо яскраві, як блискавка, відповіді. Поступово розвіється туман незрозумілого, і ми без сумніву доведемо, що заслуговуємо на успіх
Якщо запастися терпінням і проявити старання, то посіяне насіння знання неодмінно дасть добрі сходи. Навчання корінь гіркий, але плід солодкий. Тож будемо вирощувати насіння науки, щоб потім куштувати солодкі плоди наших результатів.
- Діти, що ви очікуєте від сьогоднішнього уроку?
Озвучення учнями очікуваних результатів.
III. Актуалізація опорних знань
Гра «Тягни-відповідай»
Питання:
1. Що означає риска дробу?
2. Як називається число, яке записується під рискою дробу і що воно означає?
3. Як називається число, яке записується над рискою дробу і що воно означає?
4. Які дроби називаються правильними?
5. Які дроби називаються неправильними?
VI. Повідомлення теми та мети уроку
Гра «Шифрувальник»
Розв’яжи задачі, розташуй їхні відповіді у порядку спадання і розшифруй слово, ви дізнаєтеся частину теми сьогоднішнього уроку.
И • Для букетів взяли 21 квітку. 1/3 всіх квітів – червоні. Скільки червоних квіток було в букетах? (21:3=7)
Т • На полиці 6 художніх книжок, що становить 1/3 всіх книг. Скільки всього книг на полиці. (6*3=18)
Н • Швидкість мотоцикліста 70 км/год. Весь шлях він подолав за 3 год. Яку відстань проїхав мотоцикліст? (70*3=210)
О • Автомобіль проїхав відстань 300 км за 3 год. З якою швидкістю рухався автомобіль? (300:3=100)
Відповідь: НОТИ
А для того, щоб розшифрувати друге слово теми вам необхідно розв’язати кросворд.
Робота в парах
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
- Частина прямої, обмежена двома точками (відрізок).
- Антонім до поняття «крива» (пряма).
- Геометрична фігура, яка має початок і не має кінця (промінь).
- Результат дії множення (добуток).
- Результат дії віднімання (різниця).
Відповідь: ДРОБИ
Ви розшифрували тему нашого уроку, хто назве її?
Правильно, тема нашого уроку звучить так: «Дроби та ноти». Що ж спільного між цими словами, які відносяться до різних наук? Що їх пов’язує? Саме це ми і з’ясуємо сьогодні з вами на уроці. Також узагальнимо знання про звичайні дроби, закріпимо навички виконання додавання та віднімання дробів з однаковими знаменниками та розв’яжемо задачі на знаходження дробу від числа.
А по скільки в уроці поєднані разом музика з математикою, ми повторимо види нот, їх звучання, прослухаємо мелодії та заспіваємо пісні.
V. Робота над темою та метою уроку
Математика та музика – два полюси людської культури. Слухаючи музику, ми переносимося у магічний світ звуків. Розв`язуючи задачі, ми поринаємо у логічний та точний світ чисел. Ми не задумуємося над тим, що світ звуків та простір чисел із давніх давен знаходяться поруч один з одним. А тому: «Математика й музика потребують єдиного мислення». Ці слова Енштейна стануть епіграфом сьогоднішнього уроку.
Давньогрецький філософ, математик, музикант ПІФАГОР, той самий, чиїм ім’ям названа знаменита теорема, першим побачив та об`єднав ноти з дробами. Він вивчав математичну сторону звука, шукав зв`язок між астрономією та музикою.
Ми живемо у світі звуків. Люди дуже давно навчились записувати різні звуки за допомогою спеціальних знаків. Як ці знаки називають?
Відповідь учнів: ноти.
- Скільки ви знаєте нот?
- Лунає пісня «Сім нот»
- А чи зустрічається запис дробу в музиці? Де саме?
Відповідь учнів: на початку твору після музичного ключа.

- Що стоїть перед розміром? Як називається найпоширеніший музичний ключ і чому він має дві назви?
Відповідь учнів:
- Скрипковий.
- Походить від латинської літери «G», що позначає ноту «Соль».
- А що стоїть на початку твору після музичного ключа?
Відповідь учнів: в музиці – це поняття «розмір».
- Які ви знаєте розміри в музиці? (2/4 – полька, ¾ - вальс, 4/4 - марш).
- Лунає чеська народна пісня-танець «Полька» (вчитель грає – учні співають)
Індивідуальна робота в групах
Зараз ви попрацюєте в групах, виконуючи це завдання ви закріпите знання та вміння виконувати дії з дробами.
А перед виконанням давайте пригадаємо, що при додаванні та відніманні дробів стає з чисельником та знаменником?
І і ІІ група. З ряду дробів виберіть і запишіть правильні. Який дріб називається неправильним.
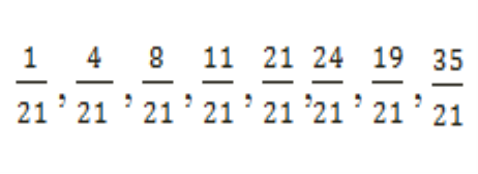
ІІІ і ІVгрупа. З ряду дробів виберіть і прочитайте правильні. Який дріб називається неправильним.
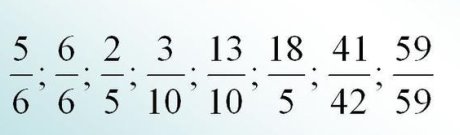
Ритмічна фізкультхвилинка (відбивання ритму)
Нотна математика
Піфагор з математичною точністю описав звук. Він зі своїми учнями помітив, що чим довша струна, тим нижчий звук, а чим тугіше натягнута струна – тим вищий. Піфагор міркував так: нота «до» - це 1(довжина основної струни), «ре» - це ½, «мі» - 1/3 і т.д.
Будиночок для нот
Опорна схема «Дроби та ноти»
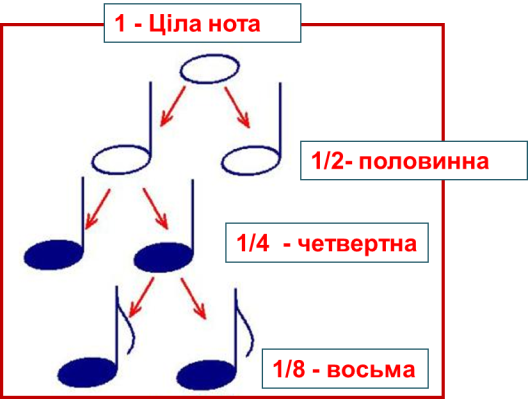
![]() Вчитель музики. То яка ж це тривалість 1 і 2 і 3 і 4 і …? Відповідь: ціла
Вчитель музики. То яка ж це тривалість 1 і 2 і 3 і 4 і …? Відповідь: ціла
![]() Вчитель математики. А ціла в математиці – це 1.
Вчитель математики. А ціла в математиці – це 1.
Вчитель музики. Коротша вдвічі від цілої тривалості: половинна
Вчитель математики. А половина в математиці – це ![]() .
.
![]() Вчитель музики. Коротша половинної: четвертна
Вчитель музики. Коротша половинної: четвертна
![]() Вчитель математики. А в математиці:
Вчитель математики. А в математиці: ![]()
Вчитель музики. Коротша вдвічі від четвертної - ![]()


Пропоную вам розв’язати музичні приклади. Перекладіть з музичної мови на математичну і виконайте дії, а потім отриману математичну відповідь перекладіть на музичну.
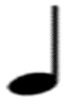


Отже, дії додавання і віднімання в музиці також існують.
Музична задача
Який урок математики без задачі? Сьогодні розв’яжемо музичну.
- Задача буде про композитора П.Чайковського – відомого композитора (демонстрація фото).
Розв’язання задачі під марш Чайковського.
• Композитор П. Чайковський написав симфонію за 800 годин. На написання І частини витратив 3/8 всього часу, ІІ частини -1/8 . Скільки годин він витратив на написання третьої частини?
![]() І частина – 3/8
І частина – 3/8
ІІ частина – 1/8 800 год
ІІІ частина – ?
- 800:8*3=300(год) – І частина.
- 800:8*1=100(год) – ІІ частина.
- 800 - (300+100) = 400(год) – ІІІ частина
Відповідь: 400 год він витратив на написання третьої частини.
Отже, розв’язавши цю задачу ми актуалізували знання і вміння виконувати арифметичні дії з дробами та знаходити частину від числа.
- Ми з вами поговорили про музичні розміри, пригадали, яким розмірам відповідають твори, це: 4/4(марш) – ми розв’язували задачу під нього, 2/3(полька) – співали та залишився останній розмір, про який ми з вами поговорили, це 3/4(вальс).
Розповідь про відомого композитора – Шопена.
Історія виникнення «Собачого вальсу».
Прослуховування «Весняного вальсу».
VI.Підсумок уроку
Наш урок підходить до завершення, тож давайте підведемо підсумки:
- Хто першим об’єднав ноти та дроби?
- Де в музиці ми зустрічаємо дроби?
- Який розмір має полька, а вальс, а марш?
- Що ще ви запам’ятали?
- Що сподобалося?
- Які з отриманих знань, умінь і навичок на уроці ви візьмете для життя?
Заключне слово
Людину можна оцінювати дробом, чисельник якого становить те хороше, що вона думає про себе сама, а знаменник те хороше, що про цю людину думають інші. То ж бажаю вам щоб дріб у кожного з вас був завжди правильним.
- Лунає пісня «Бо щастя – це…»
- Всім дякуємо за урок!
- Що означає риска дробу?
- Як називається число, яке записується під рискою дробу і що воно означає?
- Як називається число, яке записується над рискою дробу і що воно означає?
- Які дроби називаються правильними?
- Які дроби називаються неправильними?
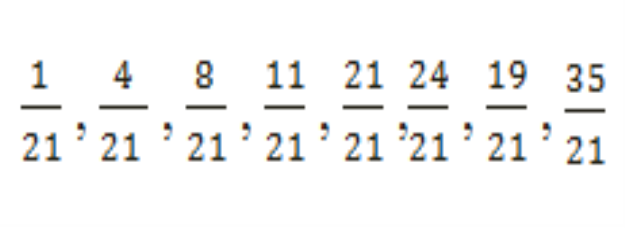
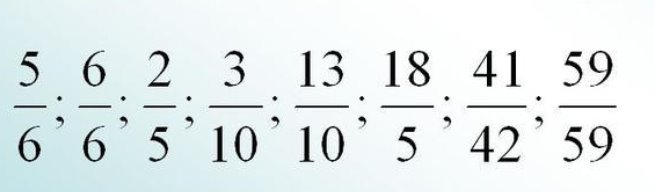


















про публікацію авторської розробки
Додати розробку
