Урок "Тема: Сума n перших членів геометричної прогресії"

Клас: 9

Тема: Сума n перших членів геометричної прогресії.

Мета:

Розвивати такі компетенції:

• спілкування державною мовами: вміння усно і письмово висловлювати поняття,  думки, факти та огляди;
• математична компетентність:уміння застосовувати математичні методи для вирішення прикладних завдань у різних сферах діяльності;
• основні компетентності у природничих науках: наукове розуміння природи і сучасних технологій; уміння застосовувати науковий метод, спостерігати, аналізувати; уміння вчитися впродовж життя;
• соціальна та громадянська компетентність: уміння працювати з іншими на результат, досягати компромісів.

Тип уроку: урок засвоєння нових знань, вмінь і навичок.

Обладнання та наочність: підручник, конспект, картки, роздатковий матеріал, шахова дошка, таблиця значень степенів чисел 2 і 3.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання. Актуалізація знань.

А) Усні запитання проведемо у формі гри «математичне доміно»

ІІІ. Мотивація навчання

1.) Вступне слово вчителя.

Учитель: Щоб зрозуміти ідею виведення формули для обчислення суми n перших членів геометричної прогресії, спочатку поговоримо про шахи.

Не дивуйтесь цьому. Шахи - одна з найдавніших ігор. Вона існує багато віків, і не дивно, що з нею пов'язані різні перекази, правдивість яких через давність часу неможливо перевірити.

3 однією з таких легенд ми сьогодні й ознайомимося. Щоб зрозуміти її, зовсім не треба вміти грати у шахи: досить знати, що гра відбувається на дошці, поділеній на 64 клітинки (чорні і білі). Шахову гру було придумано в Індії, і коли цар Шерам ознайомився з нею, він був у захопленні.

Довідавшись, що її винайшов один з його підданих, цар наказав покликати його, щоб особисто нагородити за вдалу видумку. Винахідник, його звали Сета, з'явився перед троном повелителя. Це був скромно одягнений учений, який заробляв на життя, навчаючи інших.

2.) Розігрування ситуації в ролях .

"Легенда про шахи"

Цар Шерам. Я бажаю гідно нагородити тебе, Сето, за чудову гру, яку ти придумав.(Мудрець вклонився.)

Цар. Я досить багатий, щоб виконати найсміливіше твоє бажання. Назви нагороду, яка тебе задовольнить, і ти одержиш її.

Сета. Повелителю! Накажи видати мені за першу клітинку шахівниці одну пшеничну зернину.

Цар (здивовано). Просте пшеничне зерно?

Сета. Так, повелителю. За другу клітинку накажи видати дві зернини, за третю - чотири, за четверту - вісім, за п'яту - шістнадцять...

Цар. (роздратовано перебиває Сету). Досить. Ти одержиш свої зерна, але твоє прохання недостойне моєї щедрості. Просячи таку мізерну нагороду, ти нехтуєш моєю милістю.

Учитель. Після обіду цар згадав про винахідника шахів і надіслав слугу дізнатися, чи виніс нерозсудливий Сета свою мізерну нагороду.

Цар. Чи отримав Сета свій мішок з зерном?

Слуга. Повелителю! Наказ твій виконується. Придворні математики підраховують кількість належних зерен.

Учитель. Уранці цареві доповіли, що старшина придворних математиків просить вислухати важливе донесення.

Старшина придворних математиків. Ти не можеш, повелителю, виконати таке бажання. У всіх коморах твоїх немає такої кількості зерен, яку зажадав Сета. Якщо увесь земний простір буде засіяно пшеницею. І все те, що виросте на цих полях, накажеш віддати Сеті, тоді він одержить свою нагороду.

Цар. (після паузи роздумливо). Назви ж мені це дивовижне число...

Старшина придворних математиків. 18 квінтильйонів 446 квадрильйонів 844 трильйони 73 більйони 709 мільйонів 551 тисяча 615, о повелителю!

(на дошці залишається умова до задачі і записується сума, яку повинні обчислити: ).

 Щоб розв’язати задачу, потрібно знати формулу для обчислення суми n перших членів геометричної прогресії!

ІV. Вивчення нового матеріалу.

Алгоритм виведення формули для обчислення суми n перших членів геометричної прогресії:

1) записати геометричну прогресію у вигляді, коли кожний член виражений

    через    і q;

2)скласти суму членів геометричної прогресії в загальному вигляді (отримаємо рівність *);

3) помножити обидві частини цієї суми на q (отримаємо рівність **);

4) відняти від рівності (**) рівність (*);

5) звести подібні доданки;

6) в лівій і правій частинах отриманої рівності винести спільні множники за

    дужки;

7) записати шукану формулу.

Виведення формули.

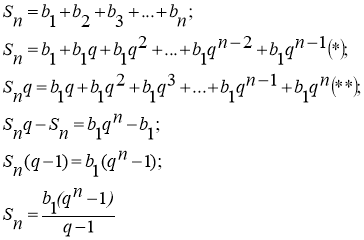
V. Засвоєння нових знань і вмінь.

1. Задача «Шахова легенда»

Розв’язання.

 :

Відповідь: Цар не зміг видати Сеті таку нагороду. Для того, щоб зрозуміти, наскільки величезним є це число, уявімо, що зерно зберігають у коморці площею 12 га. Її висота була б більшою за відстань від Землі до Сонця.

2. Задача «Купівля коня»

Дехто продав коня за 156 рублів, але покупець роздумав купувати і повернув коня продавцю. Тоді продавець запропонував йому інші умови: "Якщо по-твоєму ціна коня висока, то купи тільки цвяхи з його підков, а коня одержиш тоді на додачу безкоштовно. Цвяхів у кожній підкові 6. За перший цвях заплати мені копійки, за другий  копійки, за третій - 1 копійку і т.д."

Покупець, спокушений низькою ціною і бажаючи задарма одержати коня, прийняв умови продавця, розраховуючи за цвяхи заплатити не більше 10 руб. На скільки проторгувався покупець?

Розв’язання.

     :

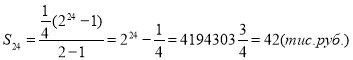
Відповідь: За таких умов можна дати і коня в додачу.

3. Робота в групах.

1 варіант №19,1(1,2); 2 варіант № 19.1(3,4)

Розв’язання.

№ 19.1 (1,2)

№ 19.1 (3,4)

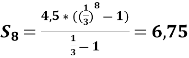
4. Самостійно. (робота з картками) Заповнити пропуски в табличці.

Нехай b, b - перший і останній члени геометричної прогресії, q-її знаменник, Sn-сума. Заповніть пусті клітинки таблиці:

1 варіант

2 варіант

Додаткове завдання

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

Розв’язання.

5 + 55 + 555 + 5555 + … = 5 ( 1 + 11 + 111 + … ) = 5 =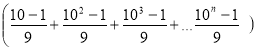

.

Відповідь: .

VI. Рефлексія

Сьогодні підсумок уроку проведемо методом «Кубування»

Вам потрібно відповісти на запитання, яке випаде на грані куба.

- опишіть, як знайти суму n перших членів геометричної прогресії?

- встановіть асоціацію з словом прогресія?

- порівняйте кількість правильних і неправильних відповідей на уроці?

- проаналізуйте відповідь ….

- застосуйте свої знання;

- поміркуйте: добре чи погано, що ви знаєте таку кількість інформації?

VII. Домашнє завдання

Опрацювати §19,

С: № 19,4

Д: № 19,6

В: № 19,10*

Творче завдання: Скласти прикладну задачу на обчислення суми n перших членів геометричної прогресії.

___________________________________

1 варіант      Заповніть пусті клітинки таблиці:

_______________________________________________________________________________________________

_________________________________

2 варіант Заповніть пусті клітинки таблиці:

___________________________________________________________________

________________________________

1 варіант      Заповніть пусті клітинки таблиці:

_______________________________________________________________________________________________

_________________________________

2 варіант Заповніть пусті клітинки таблиці:

___________________________________________________________________

________________________________

1 варіант      Заповніть пусті клітинки таблиці:

_______________________________________________________________________________________________

_________________________________

2 варіант      Заповніть пусті клітинки таблиці:

___________________________________________________________________

________________________________

1 варіант      Заповніть пусті клітинки таблиці:

_______________________________________________________________________________________________

_________________________________

2 варіант      Заповніть пусті клітинки таблиці:

__________________________________(прізвище, ім’я учня)

1. Послідовність членами якої є числа, називається __________________________

2. Прогресія, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число, називається_____________________

3. Числа 1, 3, 9, 27, 81 …… утворюють ________________________________________________

4. Запишіть формулу n-го члена геометричної прогресії__________________________________

5. Де зустрічаються числові послідовності у житті?

__________________________________________________________________________________

__________________________________(прізвище, ім’я учня)

1. Послідовність членами якої є числа, називається __________________________

2. Прогресія, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число, називається_____________________

3. Числа 1, 3, 9, 27, 81 …… утворюють ________________________________________________

4. Запишіть формулу n-го члена геометричної прогресії__________________________________

5. Де зустрічаються числові послідовності у житті?

__________________________________________________________________________________

__________________________________(прізвище, ім’я учня)

1. Послідовність членами якої є числа, називається __________________________

2. Прогресія, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число, називається_____________________

3. Числа 1, 3, 9, 27, 81 …… утворюють ________________________________________________

4. Запишіть формулу n-го члена геометричної прогресії__________________________________

5. Де зустрічаються числові послідовності у житті?

__________________________________________________________________________________

__________________________________(прізвище, ім’я учня)

1. Послідовність членами якої є числа, називається __________________________

2. Прогресія, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число, називається_____________________

3. Числа 1, 3, 9, 27, 81 …… утворюють ________________________________________________

4. Запишіть формулу n-го члена геометричної прогресії__________________________________

5. Де зустрічаються числові послідовності у житті?

__________________________________________________________________________________

__________________________________(прізвище, ім’я учня)

1. Послідовність членами якої є числа, називається __________________________

2. Прогресія, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число, називається_____________________

3. Числа 1, 3, 9, 27, 81 …… утворюють ________________________________________________

4. Запишіть формулу n-го члена геометричної прогресії__________________________________

5. Де зустрічаються числові послідовності у житті?

________________________________________________________________________________

__________________________________(прізвище, ім’я учня)

1. Послідовність членами якої є числа, називається __________________________

2. Прогресія, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число, називається_____________________

3. Числа 1, 3, 9, 27, 81 …… утворюють ________________________________________________

4. Запишіть формулу n-го члена геометричної прогресії__________________________________

5. Де зустрічаються числові послідовності у житті?

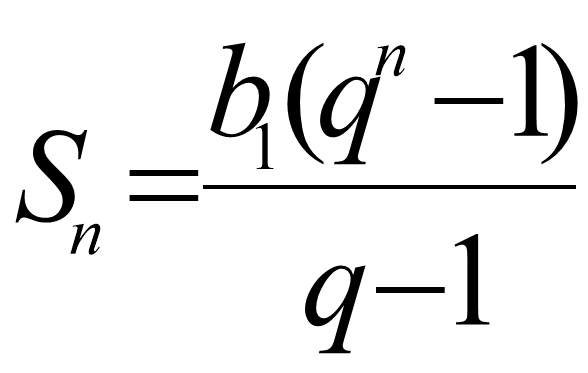
Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Знайдіть суму n чисел виду 5; 55; 555; 5555; … .

_____________________________________________________________

Повідомлення учнів «Прогресії у житті»

Будь-яка прогресія

Рухає прогрес.

До мети завітної

Вчений йде й поет.

А у математиці

Їх живе аж дві,

Додавання й множення

Здійснюють вони.

Вона і у фізиці                     

В поділі ядра

Ділить його навпіл,

Потім їх на два.

І у біології

Без її умінь

Не було б розмноження:

Вимер цілий світ!

Можна тільки крапельку

Нанести парфум,

А тоді прогресія

Зробить цілий бум!

Зранку і до вечора

Чуть приємний шлейф,

То закон прогресії

Поділ дав нам цей.

Мучився б із віршами

Кожен в нас поет,

Якби не прогресія

Ямб знайшла й хорей.

Тож вивчаймо й знаймо            

Цей закон усі,

Неодмінно будемо                

Мудрими тоді!

Закончился двадцатый век.

Куда стремиться человек?

Изучены космос и море,

Строенье звезд и вся земля.

Но математиков зовет

Известный лозунг:

«Прогресио – движение вперед!»