Урок "Теорема Піфагора"

Тема: Теорема Піфагора

Мета: познайомити учнів зі змістом та різними доведеннями теореми Піфагора, показати її застосування при розв’язуванні різних задач; виховувати інтерес до історії математики, продемонструвати зв’язок математики та інших наук.

Тип уроку: засвоєння нових знань.

Хід уроку.

І. Перевірка домашнього завдання. 

Перед початком уроку учні-консультанти перевіряють наявність домашніх робіт в учнів та допомагають тим учням, в яких виникли ускладнення під час виконання домашньої роботи. На початку уроку консультанти звітують про виконання домашньої роботи та про ті запитання, що виникали в учнів.

ІІ. Мотивація навчальної діяльності.

 У 1974 році до сузір’я Геркулес було відправлено потужний радіосигнал, який містив у собі 1679 різних повідомлень про людство, його наукові та культурні надбання, планету Земля, її хімічний склад та розміри. Серед них була зашифрована і теорема Піфагора. Дізнатись про те, чи змогли інші істоти у всесвіті розшифрувати і зрозуміти цю теорему ми зможемо дізнатися лише через 5 тис років (саме через цей проміжок часу повернеться сигнал назад на Землю). А чи зможете зрозуміти її ви, ми дізнаємося вже наприкінці уроку. Цю теорему називають вічною. Їй понад 2 тисячі років. В середньовіччя її називали «ослячим містком», тому що довести її було важко для тогочасних науковців. Тож спробуємо і ми перейти цей «ослячий місток». А епіграфом нашого уроку будуть слова Піфагора. Не роби ніколи того, що не знаєш. Але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя.

ІІІ. Історична довідка. 

1. Біографічна довідка про Піфагора Самоського. В VI столітті до н.е. у сім’ї золотих справ майстра Мнесарха народився син. За легендою, в Дельтах, куди приїхали Мнесарх з дружиною Парфенісою, - чи по справам, чи у весільну подорож, оракул пророчив їм народження сина, який буде славитися віками своєю мудрістю, справами та красою. Пророцтво збувається - в Сидоні Парфеніса народила хлопчика. І тоді за давньою традицією Парфеніса приймає ім’я Піфіада, на честь Аполлона Піфійського, а сина називає Піфагором, на честь пророцтва піфії. У легенді нічого не сказано про рік народження Піфагора; історичні дослідження датують його появу на світ приблизно 580 роком до нашої ери на острові Самос. Можливості дати сину гарну освіту та виховання у Мнесарха були. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримує знання основ музики та живопису. Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жреців. Потрапити до Єгипту у той час було дуже важко, тому що країну практично закрили для греків. За допомогою вчителя Піфагору вдається залишити острів Самос. Але поки що до Єгипту далеко. Він живе на острові Лесбос у свого родича Зоїла. Там відбувається знайомство Піфагора з філософом Ферекідом - другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим на той час наукам. Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи. Але Фалес радить йому поїхати до Єгипту, щоб продовжити навчання. І Піфагор відправляється у дорогу. Перед Єгиптом Піфагор на деякий час зупиняється у Фінікії, де, за легендою, навчається у відомих сідонських жреців. А потім йому вдається потрапити в єгипетські храми, куди чужоземців не пускали. Щоб прилучитися до таємниць єгипетських храмів, Піфагор приймає посвячення в сан жреця. Навчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу. До цього періоду відноситься подія, яка змінила все його майбутнє життя. Помер фараон Амазіс, а його наступник по трону не сплатив щорічну данину Камбізу, персидському царю, що служило достатнім приводом для війни. Перси не помилували навіть священні храми. Піддалися гонінням і жреці: їх вбивали або брали в полон. Так потрапив у персидський полон і Піфагор. Дванадцять років знаходився у вавилонському полоні Піфагор, доки його не звільнив персидський цар Дарій Гістасп, який прочув про відомого грека. Піфагору вже 60, він вирішує повернутися батьківщину. Тут і вирішує Піфагор створити власну філософську школу. Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Учні цієї школи зобов’язувались вести так званий піфагорійській спосіб життя. ...Пройшло 20 років після створення школи. Слава про неї рознеслася по всьому світу. Одного разу до Піфагора прийшов Кілон, людина багата, але зла, бажаючи в нетверезому стані вступити до школи. Піфагор відмовив і тоді Кілон розпочав боротьбу з Піфагором, скориставшись підпалом його будинку. Під час пожежі піфагорійці врятували життя своєму вчителю ціною своєї, після чого Піфагор засумував і невдовзі закінчив життя самогубством. 2. Геометричним досягнення Піфагора вважають доведення тереми про суму кутів трикутника, тракт Піфагора про многокутники та звичайно теорема, що носить його ім’я. 3. Поетична сторінка: вірш Альберт Шаміссо

Во мгле веков пред нашим взором Блеснула истина. Она, Как теорема Пифагора, До наших дней еще верна.

Найдя разгадку, мудрый старец Был благодарен небесам; Он сто быков велел зажарить И в жертву принести богам. 4. Інша назва теореми «Гекатомба», що в перекладі означає сто биків.

ІV. Вивчення нового матеріалу.

1. Формулювання теореми за Піфагором.

2. Сучасне формулювання теореми Піфагора. Його учні записують у зошитах.

3. Про цю теорему знали давно, ще 2 000 років тому. Її використовували у Стародавньому Єгипті для трикутника зі сторонами 3, 4 та 5 відрізків. (Перевірте чи справджується терема для таких сторін прямокутного трикутника).

4. На сьогодні існує близько 300 доведень цієї теореми, і мабуть Піфагор був не першим, хто довів її. Проте завдяки йому ця теорема перейшла з практичної галузі у наукову.

5. Доведемо і ми цю теорему. Спочатку геометричним способом усно. Таке доведення дійшло до нас з персидських рукописів, а замість доведення було написано лише “ДИВИСЬ!”

6. Таких геометричних доведень, заснованих на демонстрації рівності площ квадратів, побудованих на сторонах прямокутного трикутника є багато. Пропоную вам вдома спробувати один із них та отримати додаткові бали.

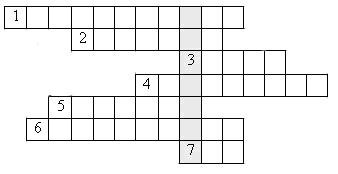
7. Актуалізація опорних знань. Для того щоб перейти до іншого способу доведення пропоную вам розв’язати такий кросворд:

1) Назва прямокутного трикутника зі сторонами 3, 4, 5. 2) Учений, ім’ям якого названа теорема про суму квадратів катетів прямокутного трикутника. 3) Острів, на якому народився цей математик. 4) Катет, який не лежить напроти даного кута. 5) Там Піфагор пробув 12 років у полоні. 6) Сторона прямокутного трикутника, яка лежить проти прямого кута. 7) Кількість биків, принесена Піфагором у жертву богам після доведення теореми.

8. Колективне доведення тереми Піфагора за підручником із записом у зошитах.

       9. Фронтальне опитування теореми Піфагора.

V. Закріплення нових знань.

1. А тепер перейшовши «ослячий місток», перейдемо до складніших задач.

Задача 1. Оскільки Піфагор був не лише філософом, а й гарним спортсменом. За легендою він приймав участь у олімпійських іграх в змаганнях з кулачного бою. І коли його не допускали до змагань з причини його невеликого зросту та похилого віку, він казав, що буде влучати в ціль з математичною точністю. Тому наступна задача спортивна.

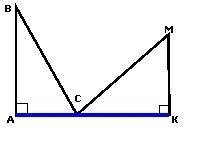
На протилежних берегах річки стоять двоє стрільців. Зріст одного 180 см, другого 120 см. Ширина річки 500 см. Обидва стрільці одночасно випускають стрілу з лука, влучаючи в один момент у мішень на поверхні води, що лежить на прямій, яка сполучає ступні стрільців. Знайти довжини шляхів стріл та місце знаходження мішені.

Розв’язання. Нехай АС = х см, тоді СК = (500 - х) см. Оскільки трикутники АВС та СКМ прямокутні, то для них справедлива теорема Піфагора. ВС2 = АВ2 + АС2, тоді ВС2 = 1802 + х2, СМ2 = СК2 + КМ2, тоді СМ2 = (500 - х) 2 + 1202. Оскільки стріли попали в ціль одночасно то СМ = ВС. Отже, маємо рівняння: 1802 + х2 = (500 - х) 2 + 1202.

Учні самостійно розв’язують рівняння (користування калькулятором дозволяється), та називають лише відповідь: х = 232. Таким чином, відстань до мішені 232 м, а довжина шляху стріли ВС2 = 1802 + 2322 = 86 224, ВС = 294 см. Відповідь: 294 см, 232 см.

Задача 2. Наступна задача суто математична, розв’язується одним з учнів біля дошки, інші конспектують її у зошит.

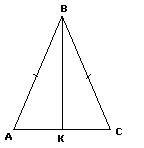
Дано: Рівнобедрений трикутник АВС, АВ = ВС = 50 м, АС = 28 см, ВК – медіана. Знайти довжину ВК.

Розв’язання. Оскільки трикутник рівнобедрений, то медіана ВК є і висотою, тому Δ АВК – прямокутний, < К = 900. АВ = 50 м, АК = 14 м (бо К – середина сторони АС). За теоремою Піфагора визначимо невідомий катет. ВК2 = АВ2 – АК2. т.т. ВК2 = 502 – 142 = (50 – 14) x (50 + 14) = 36 x 64, тоді ВК = 6 x 8 = 48 м. Відповідь: 48 м.

VІ. Підсумок уроку.

1. Фронтальне опитування теореми Піфагора.

2. Оцінювання роботи учні з аргументацією.

3. Рефлексія:

- Що сьогодні на уроці було найважливішим?

- Що на уроці було цікавим?

- Що викликало ускладнення?

- Над чим слід попрацювати вдома.

4. Попереду у вас ще багато різних теорем життєвих та геометричних, але сьогодні ви стали дорослими на цілу теорему – теорему Піфагора – цікаву, могутню, вічну.

VІІ. Домашнє завдання.

- Опрацювати п. 63

- Розв'язати

І рівень: №2 (1,3) №3 (1,3), №5

ІІ рівень: №4, №6 (1), №7

- Спробувати довести теорему Піфагора іншим способом.