Урок. "Теорема Піфагора. ( урок - подорож )"

Тема: Теорема Піфагора (Урок - подорож)

Мета: узагальнити вивчене на попередніх уроках. Перевірити набуті знання і навички учнів по даній темі; прищеплювати інтерес до геометрії; розвивати творчі й інтелектуальні здібності; виховувати вміння працювати в групах; почуття відповідальності.

Обладнання:  сигнальні картки, індивідуальні картки, картки геометричного доміно.

Тип уроку: узагальнення та систематизація знань учнів

 

Девіз уроку – слова Піфагора: «Добре засвоєна  мудрість не   забувається ніколи»

Хід уроку

Учитель. Прямокутний трикутник – одна з перших геометричних фігур, про властивості якої людство дізналося ще в давнину. Задачі про трикутник знаходять у давньоєгипетських папірусах, стародавніх індійських книгах. Сьогодні ми з вами проводимо узагальнюючий урок по темі «Теорема Піфагора», дізнаємось цікаве з історії  математики. Хочу, щоб він запам’ятався кожному з вас, щоб геометрія була вашим улюбленим предметом. Наш урок буде відбуватися в вигляді подорожі. Отже, починаємо подорож. Наша подорож буде не лише в далекі країни, але й у далеке минуле.

І етап

Острів С А М О С

Вирушаємо на острів Самос, де в 580 р. до н.е. народився давньогрецький математик Піфагор. Щоб до нього потрапити нам треба відповісти на деякі запитання. Метод «Мікрофон»

1. трикутник, у якого є прямий кут, наз….(прямокутним)
2. сторона прямокутного трикутника ,  що лежить проти прямого кута, наз….(гіпотенуза)
3. перпендикуляр, проведений з вершини трикутника на протилежну сторону , наз…(висотою)
4. відношення прилеглого катета до гіпотенузи в прямокутному трикутнику наз. …(косинусом кута)
5. відношення протилежного катета до гіпотенузи в прямокутному трикутнику наз. …(синусом кута)

Учень  Ось ми на острові Самос, де народився, найславетніший давньогрецький математик, філософ – ідеаліст Піфагор народився в 580 р. до н.е. на острові Самосі. З цієї причини його називають Піфагором Самоським. Легендарною особою Піфагора вважали у стародавні часи – у 306 р. до н.е. Вперше слава прийшла до Піфагора, коли він був юнаком. У 18 років він подорожує і їде до Мілету, щоб зустрітися з Фалесом. Фалес поділився своїми знаннями та порадив їхати до Єгипту, щоб ще повчитися у єгипетських жерців. Піфагор вирушає до Єгипту, а ми разом з ним.

ІІ етап

Є Г И П Е Т

Учитель. Ми потрапили до Єгипту. Командам по черзі задаються   питання на які вони дають відповіді.

Питання:

1. Автор теореми «Квадрат гіпотенузи = сумі квадратів катетів»

А. Евклід

В. Лагранж

C. Піфагор

D. Агата Крісті

 2. Яка національність Піфагора?

              A. Вірменин

              B. Індус

              C. Українець

              D. Грек

 3.  Єгипетський трикутник має сторони

               A.  2,  3,  4

               B.  3,  4,  5

               C.  5,  6,  7

               D.  4,  5,  6

 4.  Чому дорівнює сума кутів трикутника?

               A.  90

               B.  270

               C.  360

               D.  180

 5.  Що таке фут?

               A.  столиця Нігерії

               B.  одиниця маси

               C.  фрукт

               D.  одиниця довжини

Шкала оцінювання

Правильна відповідь на питання – 1 бал.

Учень. Єгипет – гаряча країна, тому в розподілі населення величезну роль відіграє клімат. Пустелі, екваторіальні терени заселені мало. Зате у вологих тропічних зонах та в долині Нілу люду мешкає значно більше. Ця одна з найбільших річок світу і манила до себе, і завдавала багато клопоту. Бо коли Ніл розливався і виходив з берегів, то руйнував житла єгиптян. Тому народ добре знався на будівництві і в математиці. Ще з часів подорожі Піфагора по Єгипту йому був відомий єгипетський трикутник зі сторонами 3 , 4 , 5. Піфагор провів у Єгипті 22 роки, займаючись спостереженням зоряного неба і геометрією. В той час , коли Єгипет завоював перський цар Камбіз, Піфагор був серед тих, кого захопили у полон біля стін Великих пірамід. Але його слава як мудреця і мага була вже на той час настільки велика, що коли Камбіз дізнався хто знаходиться серед його полонених, він наказав негайно звільнити Піфагора і вибачився перед вченим.

ІІІ етап

В А В И Л О Н

Після полону Піфагор переїздить . Назва цього міста зашифрована. Розв’язавши трикутники, знайдемо ключ до розв’язки.

1. Якщо катети прямокутного трикутника 3 і 4 см, то гіпотенуза…( 5)

2. Якщо катети прямокутного трикутника 12 і 13 см, то гіпотенуза…(15)

3. Знайти діагональ прямокутника, якщо його сторони 12 і 5 см. ( 13)

4. Якщо дві більші сторони прямокутного трикутника 17 і 15 см, то третя…(8)

5. Якщо катети прямокутного трикутника 6 і 8 см, то гіпотенуза …(10 )

6. Якщо катети прямокутного трикутника 15 і 20 см, то гіпотенуза …(25)

7. Якщо катет прямокутного трикутника 8 см, а гіпотенуза  10см, то другий катет …(6)

10	6	5	13	15	25	8
Л	Н	В	В	А	О	И

 

 

Учень. Після полону Піфагор перебуває у Вавилоні. Там він охоче спілкується з мудрецями і магами, які відповідали йому увагою, і , навчившись найголовнішому в його вченні глибоко опанувавши науку про числа, музику й інші предмети, провівши в такий спосіб ще 12 років.

ІV етап

І Т А Л І Я

Учитель. Ми вирушаємо на південь Італії до м. Кротоне - грецької колонії. Поки ми не прибули до місця призначення погуляємо в гру «Вірю – не вірю». всі його таємниці.  Це ми зробимо за допомогою сигнальних карток «+» або «-».

Для відповіді вам треба підняти відповідну картку. «+» - якщо твердження вірне, «-» - якщо ні. Команди по черзі аргументують свій вибір.

Твердження:

1. У будь-якому трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.(-)

2. Будь-який прямокутний трикутник  називається єгипетським?.(-)

3. Сума гострих кутів прямокутного трикутника дорівнює 180⁰.(-)

4. Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до прилеглого. (-)

5. 2 в квадраті – 4, 3 в квадраті – 9, кут у квадраті – 90? (+)

6. Трикутник з розмірами 4, 5, 6 називається єгипетським. (-)

Учень. В місті Кротоні Піфагор розпочав свою діяльність. Його вважали пророком і тому діяльність школи, яку він заснував, носила таємничий характер. Велику увагу піфагорійці приділяли дослідженням властивостей прямокутних трикутників, сторони яких визначаються цілими числами. Теорема Піфагора була відома вавилонянам ще за 1200 років до Піфагора. Знали її й у стародавній Індії. Можливо, що Піфагор або його учні дали перше повноцінне доведення цієї теореми. Теорема Піфагора є одним з найважливіших геометричних тверджень.   Відомо понад 150 способів доведення цієї теореми.

V етап

Р И Ф И

Учитель. Наші кораблі потрапили до рифів і щоб ваш корабель не сів на мілину кожному члену команди треба впоратися із завданням записаним на геометричному рифі. На виконання завдання командам дається 5 хвилин.( на дошці висять в хаотичному порядку задачі. Учні по черзі розв’язують задачі на  дошці, а останні записують їх в зошити, кожен пише задачі своєї команди, і вішають вряд картки із задачами та відповідями )

Завдання (геометричне доміно)

Командам пропонують тексти задач та варіанти відповідей до них, записані на окремих картках. Для кожної картки з умовою задачі слід відшукати картку з відповіддю. Кількість карток з відповідями більша, ніж кількість карток із задачами, тобто серед відповідей є неправильні.

Завдання 1 команди

1. Катети прямокутного трикутника дорівнюють 3см і 4см. Знайти гіпотенузу. (Відповідь. 5см.)
2. Гіпотенуза прямокутного трикутника дорівнює 13см, а один із катетів – 12см. Знайти другий катет. (Відповідь. 5см.)
3. Знайти основу рівнобедреного трикутника, якщо бічна сторона дорівнює 10см, а висота, проведена до основи, дорівнює 6см. (Відповідь. 16см.)
4. Знайти діагональ прямокутника, якщо його сторони дорівнюють 5см і 12см. (Відповідь. 13см.)
5. Сторона ромба дорівнює 13см, а одна з діагоналей – 10см. Обчислити другу діагональ.  (Відповідь. 24см.)

Завдання 2 команди

1. Знайти гіпотенуза прямокутного трикутника, якщо його катети дорівнюють 12см і 5см. (Відповідь. 13см.)
2. У прямокутному трикутнику гіпотенуза дорівнює 5см, а один із катетів – 4см. Знайти другий катет.(Відповідь. 3см.)
3. Діагоналі ромба дорівнюють 4см і 6см. Обчислити його сторону. (Відповідь. 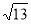см.)
4. Сторона прямокутника дорівнює 7см, а діагональ – 25см. Знайти іншу сторону прямокутника. (Відповідь. 24см.)
5. Основа рівнобедреного трикутника дорівнює 2см, а висота, що проведена до неї, - 5см. Знайти бічну сторону трикутника. (Відповідь. 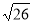см.)

Учитель. Молодці, бачу наш  екіпаж подолав і рифи і готовий подорожувати далі. Заглянемо до Німеччини.

VІ етап

Н І М Е Ч Ч И Н А

Учитель. Жителі цієї країни дуже люблять різні головоломки і загадки. От і зараз вони приготували свої сюрпризи-завдання, які ви повинні виконати за 5 хвилин.

(задачі практичного змісту)

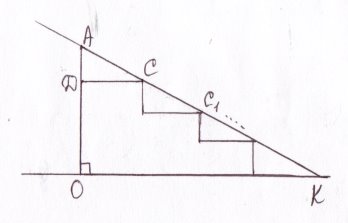
Задача 1. Ескалатор метрополітену має 160 сходинок від підлоги наземного вестибулю до підлоги підземної станції (мал.) Ширина сходинки 20см, висота – 15см. Знайдіть довжину ескалатора АВ. ( один учень розв’язує коло дошки задачу з поясненням, а інші за ним записують в зошити )

Учитель. Я вважаю, що жителі Німеччини залишилися задоволеними розв’язанням.. А ми рушаємо далі.

VІІ етап

Місто П О К Р О В

Учитель. І ось нарешті ми повернулися додому і потрапили на аукціон. Ви вибираєте одну із запропонованих задач і отримаєте бали : 6, 9, 11.

Задача 1. Катети прямокутного трикутника дорівнюють 12 м і 9 м. Знайти гіпотенузу. (відповідь:       )

Задача 2.  Основи прямокутної трапеції дорівнюють 6 см і 10 см, а більша бічна сторона дорівнює 5см. Знайти площу трапеції. ( відповідь:       )

Задача 3. Обчислити висоту рівнобічної трапеції, у якої основи = 24см і 44см, а бічна сторона – 70см.( відповідь:      )

 

Домашнє завдання : скласти задачу практичного змісту, для розв’язання якої треба використати теорему Піфагора.

Учитель. Що ж подорож закінчилася. Але подорож країнами Геометричних знань не має меж, тому що вивчати її можна без кінця. Бажаю вам  успіхів на цьому довгому і цікавому шляху!

Рефлексія

1. Які риси характеру допомагали вам досягти успіху на уроці?
2. Які заважали?

активність                                         пасивність                    упертість

дисциплінованість                            лінь                              ввічливість

неуважність                                      допитливість                недбалість    

організованість                                незібраність                 уважність

ініціативність                                   наполегливість             недбалість

відповідальність                              працелюбство