Презентація до уроку геометрії "У пошуках скарбів"
Про матеріал
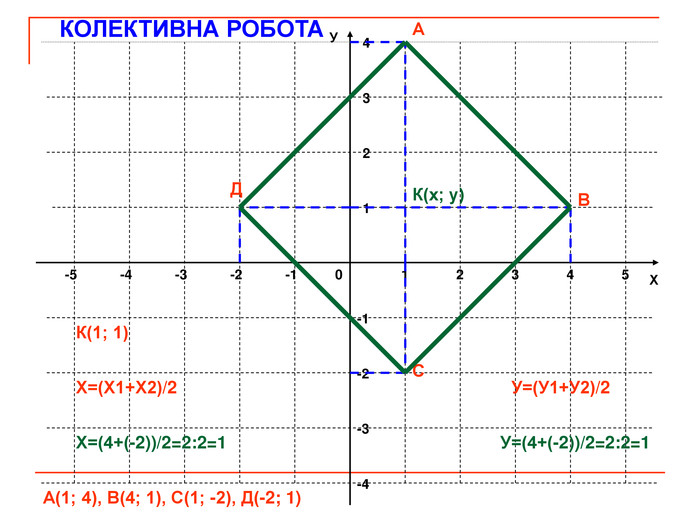
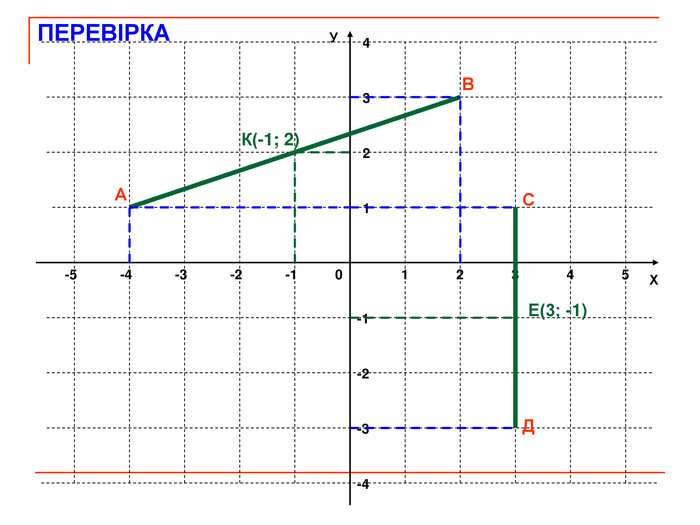
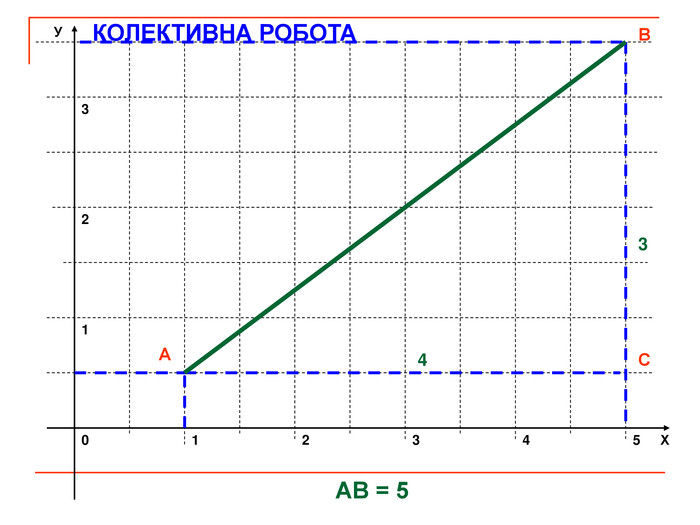
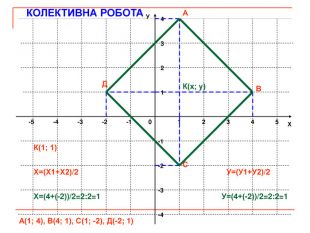
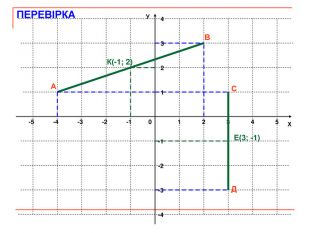
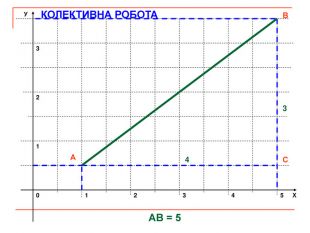
Презентація до уроку геометрії "Декартові координати на площині. Координати середини відрізка. Відстань між двома точками".
Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія 9 клас (Істер О. С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку