Урок з алгебри і початків аналізу, 11 клас (рівень стандарту)

Про матеріал

Конспект першого уроку з теми "Показникові рівняння". Тип уроку "Засвоєння нових знань, умінь і навичок". На уроці вводяться поняття нового виду рівнянь, у яких змінна міститься тільки в показнику степеня і формуються вміння і навички розв'язування найпростіших показникових рівнянь різними способами. Використано підручник А.Мерзляка "Математика" (рівень стандарту)

Перегляд файлу

Тема. Показникові рівняння

Мета. Формування в учнів навичок і вмінь розв`язувати найпростіші показникові рівняння різними способами, використовувати набуті знання на практиці; розвивати логічне мислення, творчу активність та самостійність, прищеплювати інтерес до математики; виховувати навички культури праці, вміння правильно сприймати і активно запам`ятовувати нову інформацію.

Тип уроку: засвоєння нових знань.

Обладнання: роздатковий матеріал (картки), ноутбук, опорні конспекти.

Хід уроку

І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

Два учні відтворюють розвязання вправ 1.11 і 1.13(1) на дошці з послідуючим обговоренням.

ІІІ. Актуалізація опорних знань учнів.

Учні класу відповідають на запитання:

Дайте визначення показникової функції.
Сформулюйте основні її властивості.
Схематично зобразіть графіки показникових функцій з основою а  1, 0  а  1.
Які властивості має степінь з дійсним показником?
Запишіть у вигляді степеня добутки а^хּ в^х; 3^2х ּ 3^х.
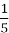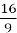
Подайте числа 5 і 0.2, 25 і , 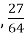у вигляді степенів з однаковими основами.

ІV. Мотивація навчальної діяльності.

Повідомлення теми і мети уроку.

Розвязування багатьох практичних задач зводиться до складання і розвязування рівнянь, у яких змінна міститься в показнику степеня. Розвязуванню деяких таких рівнянь присвятимо цей урок.

V. Вивчення нового матеріалу.

Набуття навичок і вмінь розвязувати найпростіші показникові рівняння.

Пояснення вчителя.

Показниковими рівняннями називаються рівняння, у яких змінна міститься в показнику степеня.

Вкажіть серед записаних рівнянь показникові. Поясніть свій вибір

2^х-4 = 64 2) 5^х – 4 х 5^х+2 = 99 3) 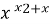= x^2х-1

4) 5^х= 6^х 5) х² = х+5

Показникові рівняння, які ми будемо розвязувати, зводяться до найпростіших рівнянь, що мають вигляд а^х = а^m, де а  0, а ≠ 1 (якщо а = 1, то рівняння має безліч розвязків).

Із змісту степеня з дійсним показником та рівності степенів з однаковими основами випливає рівність їх показників: х = m.

Під час розвязування показникових рівнянь використовують властивості степеня. Продовжити рівності:

2^2+х = 4^1-х =

(3^х)²= =

Опорний конспект 1

f(x) = g(x)

Прирівнюємо показники при рівних основах

Розвязування показникових рівнянь зведенням до однієї основи

Розвязати рівняння

5^х-1 = 25

5^х-1 = 1

5^х-1 = -5

5^х-1 = 0

5^х = 24

Розвязання

5^х-1 = 5²;

х – 1 = 2;

х = 3

5^х-1 = 5⁰;

х – 1= 0;

х = 1

Функція у – 5^хнабуває лише додатних значень, тому рівняння не має розвязків

х = log₅ 24

(будемо вчить пізніше)

2а) Робота з підручником (Математика, 11 кл. Рівень стандарту. Харків «Гімназія». 2019) № 2.1. стор.14.

Зведення показникових рівнянь до найпростіших шляхом винесення спільного множника за дужки.

Опорний конспект 2

Розвязати рівняння	3^х+2+ 3^х = 30
Винесемо за дужки спільний множник	Розвязання 3^х (3² + 1) = 30;
Виконаємо дії в дужках	3^х (9 + 1) = 30;
Розділимо ліву й праву частину на вираз в дужках	3^х ּ 10 = 30; 3^х = ;
Зведемо до однієї основи	3^х = 3¹;
Прирівняємо показники степенів	х = 1

Користуючись опорним конспектом 2 розвяжемо № 2.3 (3; 4).

Зведення показникових рівнянь до найпростіших шляхом ділення лівої і правої частин на один із степенів.

Опорний конспект 3

Розвязати ріняння	2^х-2= 3^х-2
Поділимо обидві частини рівняння на 3^х-2≠ 0	= 1
Приведемо обидві частини до однієї основи, використовуючи властивості () = ()^x; a⁰ = 1	()^x-2 = ()⁰
Зрівняємо показники і розвяжемо одержане рівняння	х – 2 = 0; х = 2