Урок з алгебри в 10 класі на тему "Найпростіші рівняння з параметром"

Тема уроку: найпростіші рівняння з параметром

Мета уроку: 1) повторити що являє собою рівняння з параметром, дати йому

                       означення, ввести поняття “контрольних” значень параметрів,

                       при яких у рівнянні відбуваються якісні зміни; розглянути

                       методи розв’язування лінійних та квадратних рівнянь з парамет-

                       рами; повторити про кількість можливих коренів лінійного і

                       квадратного рівняння;

                       формувати вміння й навички проводити дослідження щодо

                        кількості коренів лінійного (квадратного) рівняння з парамет-

                        ром,  самостійного розв’язування рівнянь з параметром;

                     2) формувати знання,  уміння й навички розв’язування рівнянь з

                     параметрами; чітко, зрозуміло виражати свої міркування аналізу-

                      ючи кількість коренів рівнянь; вчити чітко і аргументовано

                      доводити  правильність своїх дій; вчити застосувати знання при

                      розв’язуванні рівнянь з параметром

Тип уроку: засвоєння нових знань і вмінь.

Обладнання та наочність: підручник, заготовлені малюнки, заготовлені завдання, комп’ютер з інтернетом, плазма.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашніх завдань

  Розв’язати нерівності:  № 251(2)     (3х + 2) (х - 5) (4х - 1) > 0,

                                                        Відповідь: х

№ 255(1)            (4 - х) (3х + 1) (х⁴ + х² + 1) < 0,

(х⁴ + х² + 1) > 0,         Відповідь: х

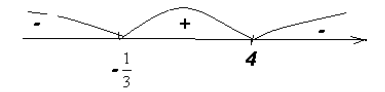
№ 265 (2)

            Нулі: 3;  7;  -1;  

        > 0,

Відповідь:   х

У.    Актуалізація опорних знань.

1. Яке рівняння називається лінійним.

2. Скільки коренів може мати лінійне рівняння  ах + в = 0:

(0х = 0;  ах = 0;   ах =  в)

3.  Яке рівняння називається квадратним.

4.  Скільки коренів може мати квадратне рівняння   ах² + вх  + с = 0:

    ( D = b² – 4ac;    D = 0;   D > 0;   D < 0. )

УІ.  Повідомлення теми і мети уроку.

УІІ. Сприйняття й осмислення нового матеріалу.

         Робота з підручником   [ 1. cтор. 94-98]

       Рівняння  з параметром – це вид алгебраїчного рівняння, в якому деякі коефіцієнти задані не числовими значеннями, а позначені літерами (параметрами) які можуть набувати будь-яких значень.

       Розв’язати рівняння з параметром означає:

1. Знайти “контрольні” значення змінних параметрів, при яких у рівнянні відбуваються якісні зміни: змінюється кількість або значення коренів.
2. Знайти всі вирази   коренів рівняння при різних значеннях параметрів.

         При знаходженні  “контрольних” значень параметрів також треба враховувати ОДЗ параметра, бо якщо його значення виходять за межі ОДЗ, то рівняння взагалі не має змісту.

         Розглянемо приклади рівнянь:

Приклад 1. ах + 31 = 0,     ах = -31,  якщо а = 0, 

то рівняння  ах = -31  (0х = -31), не має коренів,   а0,      х = .

Відповідь: 1)  а = 0,  хØ;  2) а0,  один корінь    х = .

Приклад 2.     ,         ;

;             ;

Якщо   а = 1,  то    0х = 0,    х -  будь-яке число,

якщо   а1,  то   .

Відповідь: 1)  а = 1,  х – будь-яке число; 

                  2) а1,     х = -1.

Приклад 3.   При яких значеннях параметра в має один корінь рівняння.

    2х² - вх  + 18 = 0 – це квадратне рівняння, 

D = b² – 4ac,     D = ,

 1) D = 0,    b² – 144 = 0,   b₁=-12, b₂= 12.

Відповідь: b₁=-12, b₂= 12.

Приклад 4. Розв’язати рівняння   х² - вх  - 2b² = 0.

D = b² – 4ac,   D = b² – 4(- 2b²)1= b²+8 b²= 9b²     х = .   

x = 2b;  -b.

УІІІ.  Первинне закріплення нового матеріалу.

     Робота в групах.

Розв’язати рівняння:

І група  1) ( а - 2 ) х = а + 4;

                                      Відповідь: 1)  а = 2,  хØ;                 

                                                         2) а2,     х = .

ІІ група  1) (5 - а  ) х = а + 3;

                                      Відповідь: 1)  а = 5,  хØ;                 

                                                         2) а5,     х = .

ІІІ група  1)  3 х – 4 = ах +  а;

                                     Відповідь: 1)  а = 3,  хØ;                 

                                                         2) а3,     х =

ІУ група  1)  ах - 2х = а² - 4;

                                     Відповідь: 1)  а = 2,    х – будь-яке число; 

                                                         2) а2,     х = а + 2.

ІХ. Підсумки уроку.

Х.  Домашні завдання : вчити п.13, виконати № 271, 273

                                    Використані джерела

1. Мерзляк А.Г., Алгебра і початки аналізу : підруч. для 10 кл. загальноосвіт. навч. закладів: профільний рівень / А.Г. Мерзляк, Д.А. Номіровський,

В.Б. Полонський, М.С. Якір. – Х. : Гімназія, 2010.- 416 с.

2.  О.М. Титаренко, 5770 задач з математики. 2-ге вид.,випр. – Харків:

     Торсінг, 2004. – 336с.

                            Інтернет ресурси