Урок з математики на тему: "Відношення і пропорція"

     Хмелівська ЗОШ І-ІІ ст

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Пропорція і відношення. Розв'язування вправ і задач.
                                                                                                                                            Мета:  Повторити означення пропорції та відношення, основну властивість пропорції. Формувати навички розв'язування вправ на пропорції, уміння знаходити невідомий член пропорції. Ознайомити з поняттям «золотий переріз», показати зв'язок теми з довкіллям. Розширити кругозір учнів, розвивати у них пізнавальну активність, логічне мислення. Виховувати зацікав­леність предметом, почуття колективізму, відпо­відальність за одержання колективного результату роботи, впевненість у собі.                                     

Обладнання: Картки із завданням для самостійної роботи, математичне лотто, таблиця «Пропорція і відношення», твори Баха і Бетховена, магнітофон, проектор для показу презентації, медалі-пентаграми .

Тип уроку: Повторення , систематизація знань; застосування умінь та навичок.

 

                                                                Хід уроку
І. Мотивація навчальної діяльності.

Доброго дня! Вітаю усіх присутніх! Діти! Сьогодні ми проведемо незвичайний урок. Перш ніж розпочати роботу сповістіть нам про настрій з яким ви прийшли на урок.

                  

                 Середній настрій     Поганий настрій      Гарний настрій

 

  А зараз прочитайте вислів, який буде девізом нашого уроку,

Слайд 2

      Математика - цариця наук. Її коханий - істина, її вбрання - простота та ясність. Палац цієї володарки оточений тернистими заростями і, щоб досягти його, кожному треба продертися крізь хащі. Випадковий подорожній не знайде в її палаці нічого привабливого. Краса його відкривається лише розуму, який любить істину і загартовується в боротьбі з труднощами.

     Математика створювалася людським розумом упродовж багатьох століть і продовжує розвиватися, а її застосування охоплюють все ширші кола буття. Математика - велика книга людського досвіду.

   На сьогоднішньому уроці ви дізнаєтеся тільки про одну сторінку цієї великої книги. Найкращий спосіб вивчити і запам'ятати - зробити відкриття самому. Будемо робити відкриття. А впевненості вам нададуть слова видатних людей: Слайд 3

 Хто нічого не знає, тому в нічому помилятися.

                            Менандра (342-291 до н.е.), давньогрецький поет

Щоб дійти до мети, треба перш за все йти.                    

                           Оноре де Бальзак( 1799-1850), французький письменник.

 Якщо ви боїтеся зробити помилку, не можете знайти відповіді, то згадайте ці слова ще раз і вони додадуть вам впевненості, і ви будете працювати далі.    

     Урок ми проведемо у формі гри. Ділимо клас на дві групи. Працюємо на довірі, взаємодопомога обов'язкова. За кожну правильну відповідь ви отримаєте медаль-пентаграму.

І тур «Відгадай ребус» відгадка якого є темою нашого уроку.                                             Діти відгадують ребус, лунає мелодія з твору Й.С.Баха

Слайд 4

Записуємо тему уроку у зошити: «Відношення і пропорції».                                           ІІ. Актуалізація опорних знань.

 Діти! Із поняттям «пропорція» і «відношення» ви вже ознайомлені. А чи добре ви засвоїли ці терміни ми дізнаємось, коли проведемо перехресне опитування, застосувавши метод «Мікрофон».
1група

1 учень (звертається до другого учня). Що називають відношенням двох чисел?

2 учень. Називають частку цих чисел. (До 3 учня). На що вказує відношення двох чисел?

3 учень. Вказує у скільки разів одне число більше від іншого, або яку частину становить одне число від іншого. (До 4 учня). Назвати основну властивість
відношення.

4 учень. Відношення не зміниться, якщо кожне з чисел відношення помножити або поділити на одне й теж, відмінне від 0, число. (До 5 учня) Навести приклади на основну властивість відношення.

5 учень. 6:3 = 12:6 = 18:9 = 24:12

2 група

1 учень. (До 2 учня). Продовжити речення: «Рівність двох відношень називають...»  

2 учень. Пропорцією. (До З учня). У правильній пропорції добуток крайніх членів...

3 учень. Дорівнює добутку середніх членів. (До 4 учня) Цю властивість називають.

4 учень. Основною властивістю пропорції. (До 5 учня) Щоб знайти крайній член пропорції, потрібно...

5 учень. Добуток її середніх членів поділити на інший крайній член.(До 6 учня).              А щоб знайти середній член пропорції, потрібно...

6 учень. Добуток її крайніх членів поділити на інший середній член.

 

  Отже, теорію ви засвоїли добре. Надалі ми переконаємось як вмієте ви застосовувати свої знання на практиці.

ІІІ. Розв'язування вправ.

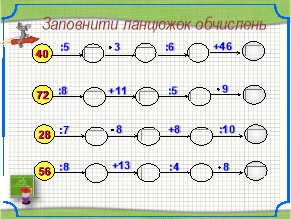
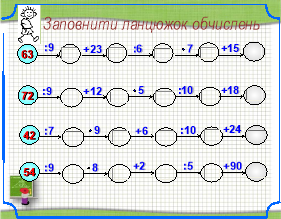
2 тур «Математичні ланцюги.»

Кожна група отримує завдання, в якому  потрібно заповнити ланцюжок обчислень, підставивши відповідні числа, Враховується швидкість і правильність виконання. До дошки йдуть по одному представнику від команди.

Слайд 5             1 група                                  Слайд 6            2 група

             

3 тур «Як ми знаємо пропорцію?» . Самостійна  робота на картках.

Слайд 7                                                    

1 група

1. Скласти пропорцію із рівних добутків 3*24 = 8*9

 

2. Чи дане відношення є пропорцією?

                16:4 = 12:3        5:6 = 25:36

                 7:2 = 3:1        10:2 = 15:3

                 3:4 = 6:8        2:10 = 4:20

3. Які рівності випливають із цих пропорцій?

                1:2 = 5:10       21:3 = 14 : 2

 

Слайд 8

2 група

      1. Скласти пропорцію із рівних добутків   6*10=4*15

      2. Чи дане відношення є пропорцією?

               9:3 = 24:8          5:2=10:4

               1:3 = 25:5          8:2=24:6

               4:6 = 6:9           1:3=4:12

     З.  Які рівності випливають із цих пропорцій?

               4:3 = 12:9         15:3 = 25: 5

Лунає мелодія з твору  Й.С. Баха.

4 тур. Задачі від старого Хоттабича.

Сьогодні в клас до нас завітав Хоттабич. Давайте привітаємо і послухаємо його!

Слайд 9

«Наймудріші юні математики! Дуже давно у вашому затишному класі я заховав цінний напій - напій мудрості. Учні, які його знайдуть і вип'ють хоч один ковток, зможуть переконатися, що вони стали кмітливішими і що їм під силу найважча задача чи приклад. Я знаю, що ви любите Старого Хоттабича .  Я вас теж дуже люблю і тому хочу, щоб ви знайшли напій мудрості. Шлях до нього - задачі з листа, які лежать у цьому конверті. Не бійтеся труднощів! Хай щастить!»

   Якщо правильно розв'яжете завдання, то вам дістанеться напій мудрості.

ЗАДАЧІ З ЛИСТА.

Слайд 10  

1-а  група

 Задача 1
Відношення   кількості   хлопчиків   до   кількості дівчаток у класі дорівнює 3          Скільки у класі учнів, якщо дівчаток 20?                                                              4                                

 Задача 2.

Том Сойєр пофарбував 1,5 м паркану, а його друг Бен - на 0,75 м більше. У скільки разів більша частина паркану, яку пофарбував Бен, від частині паркану, яку пофарбував Том?

Слайд 11

2-а  група

Задача 1

 Роки батька відносяться до років сина як 8:3. Скільки років синові, якщо батькові 48 років? 

 Задача 2.

Бригада заасфальтувала 4,2 км. дороги між двома селами, і їй залишилося заасфальтувати ще 1,8 км. У скільки разів заасфальтована ділянка довша від незаасфальтованої?

Відповідь до цих завдань вказує на шафу, де захований «напій мудрості».
Хоттабич

Молодці, що не злякалися труднощів, а дружно шукали «напій мудрості», який надає людині впевненості, сміливості і мудрості.

Вчитель.

Щоб трішки перепочити і набратись нових сил проведемо фізкультурну паузу.

 Фізкультурна пауза.
 Стоячи за партою,

  Руки на парті, пальці в кулаках,
  Зробимо вправу дітоньки так:

  Пальці стискаємо і розтискаємо,

  Мов пластилін ми усі розминаємо.
  Руки вверх ми піднімаємо,
  А на рахунок 1, 2, 3-опускаємо.
  Будемо вправу з вами кінчати,
  Легше буде тепер працювати.

5 тур.  Гра «Математичне лото» .

Слайд 12                                                                                                                                         6 тур «Логічна розминка»                                                                            «Здогадайтеся»
Як число 666 збільшити у півтора разу, не виконуючи над ним жодних арифметичних дій.

7 тур. Творчість учнів.                                                                                                                                                                                                                                        Слайд 13                                                                                                                                                     1 група.   ПРЕЗЕНТАЦІЯ ЗАДАЧІ.                                                                                                  Два рибалки разом ловили рибу. Один з них спіймав 4 рибини, а другий - 5. Коли рибалки почали смажити рибу, до них підійшов перехожий і попросив дозволу поснідати разом з ними, пообіцявши заплатити за страву. Усі троє сіли їсти, розділивши рибу на три рівні частини. Поїхавши, перехожий заплатив 90коп., подякував і пішов. Рибалки почали сперечатися, як поділити одержані гроші. Перший каже: «Мені належить 40коп., а тобі - 50», а другий каже: «Тобі належить  30 коп., а решта - мені». Хто був правий? Помиріть рибалків.

Слайд 14                                                                                                                                               2 група.     ПРЕЗЕНТАЦІЯ ПРОПОРЦЇЇ                                                                                                                 «Я не просто пропорція. На думку Луки Пачолі,навіть божественна пропорція. Грекам я замінила теорію дійсного числа і таким чином допомогла створити найкращий шедевр - геометрію. Я – душа гармонії, у мене слава архітектора, міцність споруд,чудеса мистецтва. А німецький поет і філософ Адольф Цейзинг запевняє, що я просто паную в природі».                                                                                                               Йдучи до вас, я попала під метеоритний дощ.

Х-8 = N  

  5      N

 

(х-8)25 = N* 15      Відновіть мої записи і знайдіть розв'язок                                                                                                                                                                                                

 

7 тур. Історичний.       

Що ж спільного має пропорція з музикою, архітектурою, природою…? Допоможе нам у цьому кросворд.                                                                      Слайд 15                                                                                                                      «Відгадай кросворд.»                                                                                                             1. Як називаються члени пропорції а і д? (крайні)
2. Як називають у пропорції члени в і с  (середні)
З. Як називається пропорція, значення лівої і правої частини якої є одне й те саме число? (істинна)
4. У правильній пропорції добуток крайніх членів дорівнює добутку середніх.  Як називається ця властивість? (основна)                                                                                  5. Яким математичним терміном можна замінити слово «відношення»? (частка.)

 

						1
				2
3
					4
					5

Ми знайшли одну із відповідей – це краса.

  Чому ми захоплені, коли слухаємо музику, читаємо вірші, розглядаємо витвори архітектури, живопису, дивимося на павутинку, на розташування насіння соняшника? Бо все це створено за законами краси. Виявляється, що кришталик людського ока  найкраще сприймає предмети, розміри яких перебувають у відношенні 618:1000. Таке відношення називають золотим перерізом.     Золотий переріз – гармонічна пропорція. Видатні майстри живопису Леонардо да Вінчі, Фідій, Рафаель та інші в основу своїх творінь поклали  золоту пропорцію або «золотий переріз».                                                                                                                  Й.Кеплер говорив, що геометрія володіє двома скарбами – теоремою Піфагора та золотим перерізом, і якщо перший з цих скарбів можна порівняти з мірою золота, то другий з дорогоцінним каменем – діамантом.                                                                                Слайд 18                                                                                                             Повідомлення 1. У книжці «Нулик-мореходець» розповідається про це. Існує безліч способів поділу відрізка на дві частини. Якщо даний відрізок поділити на дві частини так, що довжина більшого відрізка буде відноситись до довжини меншого як довжина всього відрізка до довжини більшого, то даний відрізок поділено у «золотому відношенні». Воно дорівнює 1,618.                                                                             

 менша частина                  більша частина                                                                              А                         В                                       С

АВ : ВС = АС : АВ = 1,618.

Історія золотого перерізу цікава і захоплююча. Вважають, що поняття золотого перерізу ввів Піфагор та його учні (у І-ст. до н. є.). Припускають, що Піфагор свої знання запозичив  у єгиптян  та  вавилонян.

Учитель.                                                                                                                            Пізніше вчені дослідили, що вся жива та нежива природа створена за законами золотої пропорції.                                                                                                               Слайд 19                                                                                                                          Розглянемо гілку горіха й оцінимо, як розміщені на ній листки. Виміряємо відстані між листками:
АВ=24.72 мм,  ВС=15.28 мм., АС=40 мм.

ТОДІ ,   АС *ВС = АВ * АВ,

              40*15.28=24.72*24.72

                611.2 = 611.1                                                                                                 

Природа - справжній знавець геометрії.

Учитель.                                                                                                                          Уявіть, що ми сіли в машину часу і опинилися в місті в епоху Відродження. Дізнаємося де ж застосовується «золота пропорція». 

Слайд 20                                                                                                                     Повідомлення 2. Майстри Стародавньої Греції вміло користувалися золотою пропорцією, використовували її гармонічні величини в усіх видах мистецтва і досягли такої досконалості побудови форм, яка рідко зустрічається в практиці
світового мистецтва.                                                                                                        Вершиною світового мистецтва вважається афінський Парфенон. Ширина Парфенона дорівнює 100 грецьким футам, висота споруди 62,8; висота колони – 38,2; висота перекриття й фронтону – 23,6. Вказані розміри утворюють ряд «золотої пропорції»

                      100 : 61,8 = 61,8 : 38,2 = 38,2 : 23,6 =1,618.

    І справді, пропорції піраміди Хеопса, храмів, барильєфів, предметів побуту і прикрас із гробниці Тутанхамона, свідчать, що єгипетські майстри
користувалися співвідношенням золотого перерізу під час їх створення.                                 

 Слайд 21                                                                                                                Повідомлення 3.   Учення про відношення і пропорції стародавні греки називали музикою, яку вважали галуззю математики. Вони знали,що чим слабше натягнуто струну, тим нижчий звук, який вона дає, а чим тугіше натягнуто струну, тим вищий дає вона звук. Але в кожному музичному інструменті є кілька струн.
   Щоб усі струни під час гри звучали приємно для вуха, довжини струн повинні перебувати в певному відношенні. Великий майстер Антоніо Страдіварі використовував співвідношення «золотого перерізу» у своїх знаменитих скрипках .

Учитель.  Ці картини, скульптури, храми для нас є зразками гармонії. Це пояснюється тим, що творці прекрасного знали досконалі, ідеальні відношення між частинами цілого, тобто відношення «золотого перерізу»                                        Людина - найдосконаліше творіння природи - створена в пропорції «золотого перерізу», які ми спостерігаємо в будові тіла, рук, кисті, ока. У середні віки вважали ідеальним тіло такої людини, для якої було характерне співвідношення «золотого перерізу».                                                                                                                             

ІV. Підсумок уроку.                                                                                                                          Ви добре працювали. Зафіксуйте у зошитах свій настрій, будь ласка, полічіть кількість набраних медалей. Виставляються оцінки. За плідну працю ви отримали медалі - це пентаграма, вона теж побудована за принципом «золотої пропорції», яка в піфагорійців вважалась символом здоров'я і щастя.(Слайд 22,23)

VІ. Домашнє завдання.                                                                                                  1.Провести конкурс краси у своїй сім'ї.                                                                                            Для цього виміряйте весь ріст, висоту тулуба з головою та довжину тіла від пояса до землі. Складіть із знайдених чисел  (у сантиметрах) відповідні відношення. Порівняйте  їх з відношеннями золотого перерізу.                                2.Повторити вивчений матеріал,  виконати домашню самостійну роботу