Урок з теми "Підготовка до ЗНО. Застосування похідної"
Тема уроку: Аналіз самостійної роботи. Похідна та її застосування.
Мета уроку:
навчальна мета:
перевірити, узагальнити, систематизувати, поглибити знання, вміння, навички учнів з теми; повторити та удосконалити знання правил і формул диференціювання елементарних функцій; систематизувати вміння учнів застосовувати набуті знання до розв’язування задач формату ЗНО;
розвивальна мета:
розвивати знання учнів про похідну і функцію, формувати навички контролю і аналізу; розвивати логічне, системне та алгоритмічне мислення, комунікабельність, увагу, пам’ять;
виховна мета:
виховувати працьовитість, наполегливість; прагнення до поглиблення та удосконалення знань; впевненість у своїх силах.
Тип уроку: урок узагальнення і систематизації знань.
Обладнання: мультимедійний проектор, екран, комп’ютери.
Перебіг уроку
І. Організаційний етап.
Перевірка готовності учнів до уроку, налаштування на роботу. Аналіз самостійної роботи: оголошення результатів, типових помилок.
ІІ. Мотивація навчальної діяльності. Формулювання цілей та завдань уроку.
Похідна і функція – фундаментальні поняття математичного аналізу, за допомогою яких досліджують процеси і явища в природних , соціальних і економічних науках. Тому повторенню цієї теми ми приділили особливу увагу.
При актуалізації знань додаються завдання ЗНО.
ІІІ. Перевірка домашнього завдання.
-фізичний, геометричний зміст похідної;
- застосування похідної в економіці;
- застосування похідної в фізиці;
Тест – самопрпевірка
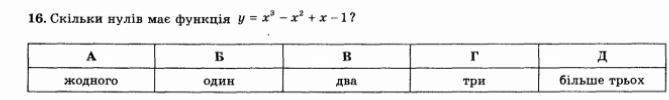

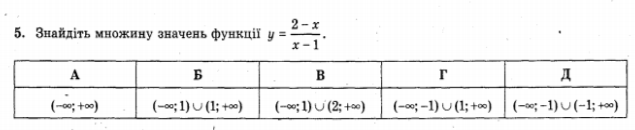

ІV. Узагальнення й систематизація знань та вмінь.
Показ слайдів на екрані, повторення основних понять, формул по ходу розв’язування вправ та задач (додатки):
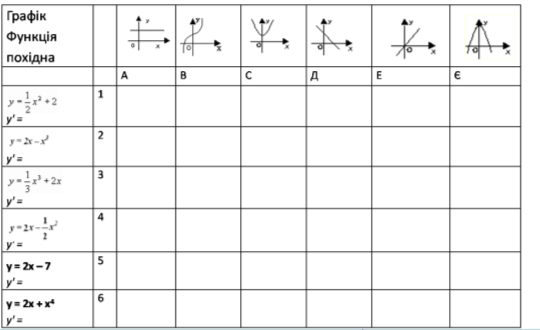
- Знайти похідні функцій (усно):
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
1 |
|
|
|
у = (3х+2)50; |
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
 2. Завдання у форматі ЗНО:
2. Завдання у форматі ЗНО:

3. Колективне розв’язування.
|
|
-
На графіку функції f(x)=
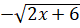 знайдіть точку, дотична в якій перпендикулярна до прямої у
знайдіть точку, дотична в якій перпендикулярна до прямої у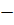 4х+5=0.
4х+5=0.
-
Матеріальна точка рухається за законом
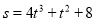 (s виміряється у метрах, t — в секундах). Знайти швидкість та прискорення в момент
(s виміряється у метрах, t — в секундах). Знайти швидкість та прискорення в момент 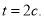
-
Матеріальна точка рухається за законом
|
Розв’язання
|
|
Відповідь: 52(м/с); 50(м/с2). |
-
При гальмуванні маховик за t секунд повертається на кут
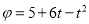 (
(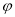 — у радіанах). Знайти: кутову швидкість
— у радіанах). Знайти: кутову швидкість 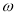 обертання маховика в момент
обертання маховика в момент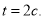 ; момент часу
; момент часу 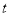 , коли обертання скінчиться.
, коли обертання скінчиться.
|
Розв'язання
Наприкінці третьої секунди кутова швидкість дорівнюватиме нулю, і обертання скінчиться. |
|
Відповідь: |
4. Розв’язування дослідницьких і практичних задач:
- Висота каменя, який підкинули вертикально вгору з швидкістю v0 і початкової висоти від землі h0 змінюється за законом х= h0+ v0 t - gt2/2, де g=10м/с2 – швидкість сили тяжіння. Знайти залежність швидкості каменя від часу.
При h0=20м, v0=8м/с. Знайти швидкість каменя через 2 с. Навіщо вказано значення h0?
Через який час камінь упаде на землю? На якій висоті швидкість обернеться в 0?
Обговорення способів розв’язання задачі:
Скласти рівняння руху - х=20+8t-5 t².
Залежність v(t) =x'(t) =8-10t.
Знайдемо v (2)=8-20=-12м/с. Знак «-» показує напрям швидкості – камінь падає вниз,в протилежному напрямку даної швидкості.
Камінь упаде на землю х=0. Час знайдемо при розв’язуванні рівняння 20+8t-5 t²=0.
Швидкість буде дорівнювати 0, коли камінь досягне максимальної висоти.
- «Яку з чашок вигідніше купляти?». Звісно дешевшою є та, на яку іде менше матеріалу. Для цього дослідимо чашки циліндричної форми.
Математично задача звучить так: який із циліндрів з периметром осьового перерізу Р має найбільшу бічну поверхню?


Отже, найбільшу бічну поверхню має циліндр, у якого осьовий переріз –квадрат.
5. Індивідуальна робота учнів за картками:

V. Підсумки уроку.
1. Рефлексія.
На початку уроку була поставлена
мета. Чи досягли її?
Продовжити речення:
- сьогодні на уроці я навчився…
- сьогодні на уроці я повторив…
- уроком я (не) задоволений…
- Хвилинка корисних порад
-
Використовуйте принцип "Бритва Оккама". Принцип стверджує, що не треба робити більше припущень, ніж мінімально потрібно. Не ускладнюйте життя там, де воно просте!
2. Будьте уважні! Доведено, що більшість помилок допускається, коли неуважно читаєш умови завдання. Тому вдумайся у суть завдання, кілька разів перечитай його умову перед тим, як відповідати.
3 . Користуйтеся принципом штангіста. Потрібно спокійно ставитися до того, що в тестах ЗНО можуть бути ті задачі, які складно розв'язати. Це нормально. Якщо є така "штанга", яку складно підняти, боятися і комплексувати з цього приводу не потрібно!
4. Кажуть, щастить завжди сильнішим, а на ЗНО - підготовленим. Вірте в свої сили та вміння! Недарма на підготовку до іспиту пішло багато часу.
Фортуна посміхається тим, хто добре працював!
VІ. Домашнє завдання:
Повторити формули знаходження похідних;
розв’язати завдання (учні індивідуально обирають відповідно рівням навчальних досягнень, записують умови завдань):
 Додатки
Додатки



Література
1.Нелін Є.П. Алгебра і початки аналізу: підручник для 11 кл. загальноосвітніх нівчальних закладів, -Х.:Світ дитинства, 2006.
2. Старова О.О., Маркова І.С., Готуємося до підсумкової атестації, ЗНО:посібник для вчителя. –Х.: «Основа», 2008.
3. Роганін О.М. Тест-контроль, алгебра, геометрія. Поточне, тематичне, річне оцінювання.-Х.: Весна, 2009.
4. Бабенко С.П. Уроки алгебри, 11 кл.,-Х.:Основа, 2011.
5. Малюкова А. А. Методична розробка уроку математики для 11 кл.
6. Узагальнюючо-підсумковий урок по темі “Похідна функції».
Uroki/090_pokhidna_urok.doc
7. Плани-конспекти. Освіта і Наука. http://firstedu.org.ua/index.php.
8. https://shag.com.ua/urok-seminar-meta.html


про публікацію авторської розробки
Додати розробку
