Урок "Закони геометричної оптики"

Тема уроку: ЗАКОНИ ГЕОМЕТРИЧНОЇ ОПТИКИ

Мета уроку: повторити з учнями зміст законів геометричної оптики, до­повнивши й поглибивши їх.

Тип уроку: урок вивчення нового матеріалу.

 Демонстрації: 1. Прямолінійне поширення світла.

2. Відбивання світла.
3. Заломлення світла.

План викладення нового матеріалу:

1. Основні поняття геометричної оптики

2. Закон прямолінійного поширення світла.

3. Закон відбивання світла.
4. Закон заломлення світла.

Хід уроку

І. Привітання.

ІІ. Перевірка присутності учнів.

ІІІ. Перевірка готовності учнів до уроку.

IV. Викладення нового матеріалу.

1.        Основні поняття геометричної оптики.

На з'ясування природи світла знадобилося не одне тисячоліття. За цей час багато різних гіпотез змінили одна одну. Оптика (від грец. орtiке — наука про зорові сприйняття) спо­чатку розглядалася як наука про зір. У наш час оптика являє собою розділ фізики, в якому вивчаються явища та закономірності, пов'язані з виник­ненням, поширенням і взаємодією з речовиною електромагнітних хвиль видимого діапазону.

Оскільки світло — електромагнітне випромінювання і йому притаман­ні усі властивості електромагнітних хвиль, то всі завдання оптики можна розв'язати на основі хвильових уявлень. Однак це вимагає застосування надто громіздкого математичного апарату. Тому під час розв'язування за­дач на побудову зображень у дзеркалах і лінзах, а також проведення роз­рахунку оптичних приладів учені користуються методами геометричної оптики, яку ще називають променевою оптикою.

Геометричною оптикою називається розділ оптики, в якому ви­вчаються закони поширення світлової енергії в прозорих середовищах на основі уявлення про світловий промінь.

Геометрична оптика базується на трьох законах:

• закон прямолінійного поширення світла;
• закон відбивання світла;
• закон заломлення світла.

Основними поняттями геометричної оптики є пучок і промінь. У першому наближенні пучок променів — це сукупність світлових про­менів.

Якщо пучок променів виходить із однієї точки або сходиться в одній точці, то він називається гомоцентричним. Розбіжний, збіжний і пара­лельний пучки світла є гомоцентричними.

У сучасній фізиці під світловим променем розуміють достатньо вузь­кий пучок світла, який у межах зони, в якій вивчається його поширення, можна вважати не розбіжним.

Оскільки світло, як і будь-яке випромінювання, переносить енергію, то можна говорити, що світловий промінь указує напрям перенесення енер­гії світловим пучком.

Не існує нескінченно вузьких світлових пучків; пучок світла завжди має скінченну ширину. Промінь — це вісь пучка.

Закони геометричної оптики вивчалися на дослідах у 8 класі. Нагадає­мо учням вивчене раніше, трохи доповнивши та поглибивши їх знання.

2.        Закон прямолінійного поширення світла.

Деякі із законів оптики були відкриті задовго до того, як була встановлена природа світла. Одним із таких законів є закон прямолінійного поширення світла:

світло в оптично однорідному середовищі поширюється прямолі­нійно.

Оптично однорідним вважається таке середовище, в якому світло поши­рюється зі сталою швидкістю. Якщо є два середовища, в яких світло поши­рюється з різними швидкостями, то середовище, де світло поширюється з меншою швидкістю, називають оптично більш густим, а середовище, де світло поширюється з більшою швидкістю,— оптично менш густим.

Прямолінійність поширення світла підтверджується утворенням тіні. Якщо взяти невелике джерело світла, екран і між ними помістити непрозорий предмет, то на екрані з'явиться темне зображення його об­рисів — тінь.

Тінь — область простору, до якої не потрапляє енергія від джерела світла (або інакше: область простору, з якої не можна побачити джере­ло світла ).

Якщо джерело світла протяжне, то на екрані навколо тіні утвориться півтінь.

Півтінь — область простору, до якої енергія від джерела світла по­трапляє частково (або інакше: область простору, з якої джерело світла можна побачити лише частково).

Утворенням тіні й півтіні пояснюються сонячні й місячні затемнення. Під час сонячного затемнення повна тінь від Місяця падає на Землю. З цьо­го місця земної поверхні Сонця не видно. Коли Місяць, обертаючись нав­коло Землі, потрапляє в її тінь, то спостерігається місячне затемнення.

У тих місцях планети, куди впала тінь, буде спостерігатися повне со­нячне затемнення. У місцях півтіні тільки частина Сонця буде закрита Місяцем, тобто відбудеться його часткове затемнення.

3.        Закон відбивання світла.

З відбиванням світла ми стикаємося що­дня: день у день кожний із нас дивиться на себе в дзеркало; ми бачимо на спокійній поверхні води зображення Сонця й Місяця, дерев і хмар. Це приклади дзеркального відбиття світла.

Якщо спрямувати вузький світловий пучок на поверхню води у великій посудині, то частина світла відіб'ється від поверхні води, інша частина пройде з повітря у воду. Під час поділу світлового пучка виконується за­кон збереження енергії.

Зобразимо розглянутий дослід графічно (рис. 1). Лінія МN — пер­пендикуляр до межі поділу двох середовищ. Промінь S — падаючий; про­мінь S1 — відбитий; промінь S2 — заломлений. Кутом падіння (α) на­зивається кут між падаючим променем і перпендикуляром, опущеним у точку падіння. Кутом відбивання (β) називається кут між відбитим променем і тим самим перпендикуляром. Кутом заломлення (γ) нази­вається кут між заломленим променем і перпендикуляром МN.

Закон відбивання світла, як і закон прямолінійного поширення світла, був відкритий давньогрецьким ученим Евклідом.

На основі експерименту (використовуючи рис. 1) сформулюємо закони відбивання світла:

• промінь падаючий і промінь відбитий лежать в одній площині з пер­пендикуляром, опущеним до відбиваючої поверхні у точці падіння;
• кут падіння дорівнює кутові відбивання.

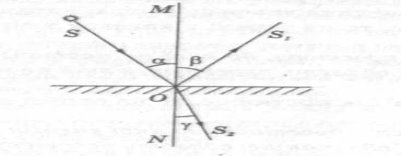
Рис. 1.

4.        Закон заломлення світла.

Вивчення заломлення світла почнемо з по­вторення дослідів з одночасного відбивання та заломлення світла на межі розділу двох прозорих середовищ. При зміні кута падіння пучка спосте­рігається зміна яскравості відбитого та заломленого пучків — яскравість одного збільшується, а іншого зменшується. Якщо кут падіння пучка світла на плоску межу дорівнює нулю, то заломлення немає. Зі збільшен­ням кута падіння зростає й кут заломлення.

Заломлення світла пояснюється зміною швидкості поширення світла, під час його переходу з одного середовища в інше.

Історики науки приписують експериментальне відкриття закону залом­лення світла в його сучасному вигляді голландському вченому В. Снелліусу (1621 p.), однак теоретичне обґрунтування цього закону було здійснене французьким фізиком і математиком Р. Декартом (1630 p.).

Використовуючи демонстраційний експеримент і креслення, форму­люємо закони заломлення світла:

• промінь падаючий і промінь заломлений лежать в одній площи­ні з перпендикуляром, опущеним до межі розділу двох середовищ у точці падіння;
•          відношення синуса кута падіння до синуса кута заломлення для да­них двох середовищ є величина стала, залежна тільки від оптичних властивостей цих середовищ:

,

де - відносний показник заломлення другого середовища відносно першого.

V. Запитання до учнів у ході викладення нового матеріалу

1. Які приклади ви можете навести на підтвердження прямолінійного поширення світла?

2. Чому утворення тіні є доказом прямолінійності поширення світла?
3. Що таке тінь і півтінь?

4. Які явища відбуваються під час переходу світла з одного середовища в інше?

5. Чим зумовлене заломлення світла на межі розділу двох прозорих сере­довищ?

6. У якому випадку відносний показник заломлення є більшим за одини­цю? В якому — меншим за одиницю?

VI. Задачі для розв'язування на уроці.

1. Ви стоїте на березі річки. На протилежному березі росте дерево, висота якого вам відома. Опишіть спосіб, за допомогою якого можна виміряти ширину річки, якщо у вашому розпорядженні є лінійка з поділками.

Розв'язання. За допомогою лінійки треба виміряти довжину витягну­тої руки (позначимо цю довжину l). Потім, тримаючи лінійку у витягну­тій руці (рис. 2), треба «виміряти» видиму «висоту» дерева (позначимо її h). Тоді ширина річки L обчислюється з пропорції
, де Н — висота дерева. Під час розрахунків можна знехтувати довжиною руки в порівнянні з шириною річки.

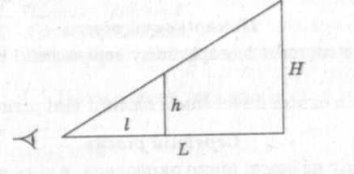
Рис. 2.

2. Сонячного ранку постать людини зростом 180 см відкидає тінь зав­довжки 4,5 см, а дерево — тінь завдовжки ЗО см. Чому дорівнює висота дерева? (Відповідь: 12 м.)
3. Сонце заходить за пагорб, на вершині якого стоїть поодинока сосна заввишки ЗО м. На якій відстані від сосни перебуває людина, якщо їй здається, ніби висота сосни дорівнює діаметрові сонячного диска? (Від­повідь: 3,2 км.)

VII. Домашнє завдання.

Підготуватися до самостійної роботи.