Дніпровська гімназія №143

Дніпровської міської ради

 

 

 

 

 

 

 

 

 

 

 

Урок алгебри в 11 класі

 

 

 

Застосування похідної до розв’язування 

прикладних задач

 

(урок – конференція)

 

 

 

 

 

 

 

 

Вчитель: Терещенко Тетяна Всеволодівна

 

 

2023 рік

 

Урок з алгебри (11 клас)

Тема уроку. Застосування похідної до розв’язування прикладних задач

 «Серед усіх наук, які відкривають шлях до пізнання

природи, найвеличнішою є математика» С. Ковалевська

Мета навчальна: узагальнити, розширити знання з теми «Застосування похідної» на прикладах розв’язування задач практичного змісту, формувати уміння і навички розв’язувати задачі на знаходження найбільшого і найменшого значення функції, орієнтувати учнів на виявлення та вивчення багатогранності зв’язків між математикою та іншими предметами; розвиваюча: стимулювати розвиток логічного і творчого мислення, уміння аналізувати, робити висновки, узагальнювати данні, використовувати отриману інформацію в особистому житті; виховна: виховувати допитливість, активність, дисциплінованість, охайність ведення записів, прагнення до самоосвіти, інтерес до математики як засобу пізнання навколишнього світу і дбайливе ставлення до природи.

Завдання: розширити компетентності учнів щодо застосування апарату диференціального обчислення до моделювання реальних життєвих процесів; впроваджувати інформаційно-комунікативні технології та презентаційні матеріали.

          Тип уроку: урок удосконалення знань, формування практичних умінь.

          Вид уроку: урок-конференція 

Обладнання: комп’ютер, мультимедійна дошка, портрети математиків.

Структура уроку з хронометражем:

1.      Організаційний етап 1хв.

2.      Мотивація навчальної діяльності 4хв.

3.      Наукова конференція 80хв.

Виступи кафедр: історії (7хв), біології (7хв), хімії (7хв), математики (8хв), фізики (14хв), медицини (7хв), архітектури та будівництва(15хв), іноземної філології (5хв). Питання від слухачів (самостійна робота) 10хв.

4.      Підсумок уроку. Рефлексія. Домашнє завдання 5хв.

 Підготовка:  учні готуються до уроку заздалегідь: добирають задачі, готують презентації з даної теми, шукають історичний матеріал, прислів’я.

ХІД УРОКУ

1.   Організаційний етап. Учні займають свої місця в групах за столами, на яких знаходяться таблички з назвами кафедр: історії, біології, хімії, математики, фізики, медицини, архітектури та будівництва, іноземної філології.

2.   Мотивація навчальної діяльності. Вступне слово вчителя.

Добрий день, вітаю всіх присутніх! І перед початком нашої роботи я хочу повідати вам сучасну притчу.

Звернувся бізнесмен до мудреця: «О, найвеличніший і наймудріший! Прийшов я до тебе за порадою. Зростають ціни на пальне. Порадь мені, будь-ласка, як організувати доставку товарів, щоб витрати палива були найменшими?».

Мудрець за велику винагороду сказав йому два чарівних слова.

 Прийшов до мудреця конструктор: «Порадь, найвеличніший і наймудріший, як добитися найменшої маси конструкції, не зашкодивши її міцності?». Мудрець і йому сказав два чарівних слова.

 Завітав до мудреця еколог: «О, найвеличніший і наймудріший! Благаю, допоможи спасти людство. Атмосфера так швидко забруднюється продуктами життєдіяльності. Як зменшити цей вплив?». Мудрець і йому сказав незмінні два чарівних слова. 

Хто б не звертався до мудреця за порадою: фермер чи лікар, електрик чи генетик, мандрівник чи домогосподарка, нікому не відмовив старець. Всі дізнались, що треба робити. 

Час підняти таємничу завісу. Ці чарівні слова знаємо і ми. «Вивчайте похідну!» – сказав їм мудрець. Дійсно, знання похідної допомагає розв’язати багато практичних задач на знаходження оптимального результату.

І тому дозвольте мені відкрити засідання наукової ради, тема якого «Застосування похідної до розв’язування прикладних задач». Ми розглянемо, як можна застосовувати апарат диференціального обчислення до моделювання і оптимізації реальних життєвих процесів в різних галузях науки і техніки. 

На цьому засіданні присутні представники кафедр: історії, біології, хімії, математики, фізики, медицини, будівництва та архітектури, іноземної філології; представники преси, спостерігачі та фахові консультанти.

3. Наукова конференція 

Секретар: Пропоную розпочати роботу наукової ради. Слово надається представникам кафедри історії, які повідають нам легенду про одну з найдревніших задач, пов’язаних з пошуком форми лінії, яка обмежує найбільшу площу. (слайд «Кафедра історії»)

Перший представник кафедри розповідає легенду «Задача цариці Дідони». Цікавою є легенда про відшукання найбільшого значення функції, за якою засновниця м. Карфагена Дідона, дочка царя тирів, посварившись з братом Пігмаліоном, втекла від свого батька і після багатьох пригод з’явилася на південному узбережжі Середземного моря. Тут, у царя Нарбаса, за невеликі гроші вона купила шматок землі «не

більше, ніж можна обміряти шкурою бика» – як зазначалося в угоді. Місцеві жителі вважали умову буквальною і розраховували, що Дідоні для нового поселення дістанеться дуже маленький клаптик узбережжя. Проте спритна Дідона розрізала шкуру бика на найтонші смужки, зв’язала їх мотузкою і, закріпивши один її кінець на березі моря, пішла з іншим вздовж берега. Перед нею постало питання: яку форму потрібно надати мотузці, щоб «обміряти шкурою бика» найбільшу площу? Зокрема, це є задача на пошук замкненої кривої даної довжини, що обмежує найбільшу площу. Виявляється, що такою кривою є коло. Дідоні, щоб розв’язати задачу, потрібно було обійти півколо з центром у точці О, довжина якого дорівнювала довжині мотузки. Дякую за увагу.

Питання преси: Наші читачі цікавляться, завдяки кому і коли стало реальним застосування певних математичних дій для вирішення таких проблем?

Представник кафедри історії доповнює. (слайд «Творці математичного

аналізу»)

До відкриття похідної незалежно один від одного прийшли два відомих вчених англійський фізик та математик Ісаак Ньютона та німецький математик і філософ Го́тфрид Ви́льгельм  Лейбніц.

Виникнення математичного аналізу не випадково припадає саме на XVII століття. У цю епоху розвиток науки та техніки дійшов тієї межі, коли для подальшого просування вперед необхідно було глибше проникнути у суть речей, вивчити закони природи та процеси, що відбуваються в навколишньому середовищі.

Всі процеси протікають з певною швидкістю, всі величини, що беруть участь у цих процесах, змінюються, причому вони взаємозв'язані. Тому постала необхідність у такому апараті, за допомогою якого можна було б вивчати змінні процеси. Саме такий апарат і був розроблений у математичному аналізі. Таким чином, виникнення диференціального числення було історично неминучим: цього вимагали потреби механіки, фізики та астрономії. За допомогою диференціального числення було розв’язано цілий ряд задач. Зокрема, вчені передбачили повернення комети  Галлея, що стало тріумфом  науки XVIIІ століття.

Секретар: Дякуємо представникам кафедри історії за екскурс в минуле та надаємо слово представникам кафедри біології. (слайд «Кафедра біології»)

Задача 1. У живильне середовище вносять популяцію з 1000 бактерій. Чисельність популяції зростає за законом:

р(t) 10001001000^t^t₂ ,

2

де t - виражається в годинах. Знайти максимальний розмір цієї популяції.

 

Представник кафедри розв’язує на дошці задачу, всі записують розв’язок в зошитах, в процесі розв’язування учні мають право задавати питання. Розв’язання

                Розглянемо дану залежність, як функцію, у якої змінною величиною є час t.

Областю допустимих значень змінної є множина додатних чисел (t>0).

          Знаходимо похідну даної функції:

                                                                    1000(100t²) 2000t²     1000001000 t²

                                                  р(t)           (100     2)2                         (100t2)2          ;

t

         Після спрощення прирівнюємо похідну до нуля і знаходимо критичні точки функції.

      р(t)  0, 100000(1001000t2)2 t²  0, _100100000_t2_10000,   t²  0, __tt²2 _100_100, , t1 10,        t2  10 ;

Від’ємне значення змінної не задовольняє ОДЗ.

Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

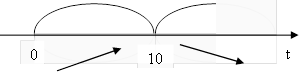
                                                                                                              (max)                                

 Отже через 10 годин чисельність популяції бактерій буде мати максимальний розмір, який становитиме: р(10) 1000  1050 (бактерій).

Питання біологам: Чому вас зацікавили саме бактерії?

Відповідь: Бактерії – це найпоширеніша група організмів (половина біомаси Землі). Серед них є як шкідливі, так і велика кількість корисних видів. Через їх здатність швидко рости і відносну легкість, з якою ними можна маніпулювати, бактерії широко використовуються у молекулярній біології, генетиці та біохімії. Вчені досліджують ДНК бактерій, а потім застосовують ці знання до більш складних організмів.

Секретар: Дякуємо представникам кафедри біології і дізнаємось, над чим працювала кафедра хімії? (слайд «Кафедра хімії»)

Задача 2. Газова суміш складається з окису азоту і кисню. Потрібно знайти концентрацію кисню, при якій окис азоту в

суміші    окислюється        з        найбільшою швидкістю? 

Представник кафедри розв’язує на дошці задачу.

Розв’язання

         В    практичних    умовах    швидкість    реакції    2NO+O₂=2NO₂    виражається

формулою: V  kx²y , де х – об’ємна  концентрація  NO, у – об’ємна концентрація O₂ в будь-який час, k – константа швидкості реакції, яка залежить тільки від температури. Якщо прийняти об’єм суміші за 1, то х+у=1. Змінними величинами є концентрації складових суміші. Області допустимих значень змінних є:  0<x<1, 0<y<1. Виразимо одну змінну через іншу: х=1–у, тоді швидкість реакції буде:

V(у)  k(1 у)² y  k(у  2у²  у³) .

Знаходимо похідну даної функції: V(у)  k(1 4у  3^у2). 

Прирівнюємо похідну до нуля і знаходимо критичні точки функції.

                                                      V(у)  0,    k(1 4у 3у²)  0,     3у²  4у 1 0,

отже, маємо квадратне рівняння,   корені якого:

D  4² 4311612  4  2²,           y₁  ^42  ¹, y₂ 1 – не задовольняє ОДЗ.

                                                                                                       6        3

          Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

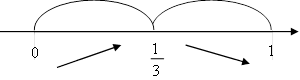у

                                                                                                             (max)                                   

 Отже, окис азоту в суміші окислюється з найбільшою швидкістю, якщо об’ємна  концентрація кисню становить  об’єму.

Питання хімікам: Чому ви обрали для дослідження саме таку реакцію?

Відповідь: Окис азоту представляє собою сильний і небезпечний ядовитий газ, який викидається в атмосферу і впливає на екологічне становище. На очисних спорудах для повного поглинання окислів азоту з газових сумішей необхідне попереднє окислення NO до NO₂, що ми і пропонуємо зробити найбільш ефективно.

Секретар: Дякуємо представникам кафедри хімії за надію, що дихати нам буде легше і передаємо слово математикам, які познайомлять нас з азами економії.

(слайд «Кафедра математики»)

Представник кафедри математики: «На нашу кафедру надійшло замовлення від підприємця. Виходячи з цього завдання, ми склали задачу і розв’язали її». Задача 3. Зробити розрахунки розмірів консервної банки циліндричної форми об'ємом 1000см³, щоб   витрати     жерсті       на      її виготовлення були мінімальними. Розв’язання

Консервна банка має циліндричну форму, отже її об'єм задається формулою:

V R²H . Змінними величинами є висота

банки Н і її радіус R. Області допустимих значень змінних є множини додатних чисел (Н>0, R>0). Щоб перейти до однієї змінної, виразимо висоту через радіус і

                                  V      1000

об'єм: Н  R₂  R2 . Витрати жерсті будуть мінімальними, коли площа поверхні циліндра буде найменшою. Отже маємо вираз, що визначає цю площу: Sпп  2RH  2R2  2^RR¹⁰⁰⁰2  2R2  ²⁰⁰⁰_R  2R2 .

_

Знаходимо похідну даної функції:

                                                                                                    2000              4R³  2000

                                                                Sпп (R)   R2  4R  R2          .

                    Прирівнюємо похідну до нуля і знаходимо критичні точки функції.       

                                                                               4R³  2000         4R³  2000  0,

                                          S_пп (R)  0; R₂  0; _R  0;                   

      R3  500 , R  3 3500,14, R  5,42(см). Н  VR2        R2  3,145,422 10,8(см).

 

         Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

R

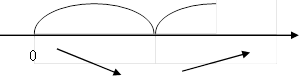5,42 (min)

 

 Отже, при R≈5,42см і Н≈10,8см витрати жерсті на виготовлення банки будуть мінімальними.

Питання математикам: Як форма банки впливає на результат ваших досліджень?

Відповідь: При зміні форми банки потрібно обрати відповідні формули для знаходження її об’єму і площі поверхні, а далі аналогічні кроки.

Секретар: Дякуємо представникам кафедри математики. Цікаво, якими відкриттями поділяться з нами фізики? (слайд «Кафедра фізики»)

Задача 4. Дощова крапля падає під

дією сили   тяжіння,    рівномірно випаровуючись так, що її маса змінюється

2t

                                                                                                         за законом:           т 1   

30

(m - в грамах, t - в секундах). 

Через який час після початку падіння кінетична енергія краплі буде найбільшою? Розв’язання

 Швидкість вільного падіння зростає з часом за законом v  gt , тоді кінетична енергія буде змінюватись з часом відповідно:

Ек(t)  mv2 1 2t  g2t2  g2t2  g2t3 .



                                                                                          2          30   2          2        30

Розглянемо дану залежність, як функцію, у якої змінною величиною є час t.

Областю допустимих значень змінної є множина додатних чисел (t > 0).

          Знаходимо похідну даної функції:

                                                                                                 2g2t      3g2t2

                                                                          Ек(t)                 g2t1 t .

                                                                                                    2         30               10

Прирівнюємо похідну до нуля і знаходимо критичні точки функції. Е_к(t)  0, g^2t1^ t _ 0, t₁ 10(c), t₂  0 – не задовольняє ОДЗ.

                                                            10

Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

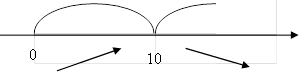t

                                                                                                              (max)                                   

Отже, кінетична енергія краплі буде найбільшою через 10с після початку падіння.

Питання фізикам: Навіщо треба обчислювати кінетичну енергію дощу?

Відповідь: Кінетична енергія падаючих крапель, яка за рахунок тертя передається в атмосферу у вигляді тепла, є сильно недооціненим джерелом кліматичних змін на Землі. Глобальне потепління вимагає саме таких досліджень. Задача 5. Корисна потужність, що виділяється на      реостаті,   задається формулою Р(R) UI  I²R  (R^²Rr)₂ .

2

При якому зовнішньому опорі R корисна потужність джерела струму буде максимальною? 

Розв’язання

Розглянемо дану залежність, як функцію, у якої змінною величиною є зовнішній опір R. Областю допустимих значень змінної є множина додатних чисел (R >0).

          Знаходимо похідну даної функції:

²(Rr)² ²R2(Rr) ²(Rr)(Rr 2R) ²(r  R)

                     Р(R)                (Rr)4                                       (Rr)4                          (Rr)3 .

Прирівнюємо похідну до нуля і знаходимо критичні точки функції.

                                                                                           ²(r  R)          r  R  0,

                                                          Р(R)  0, (R  r)₃  0, _R _ r _ 0,        R  r.

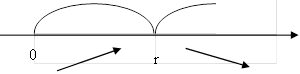
Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

R

(max)

 

Отже, корисна потужність джерела струму, що виділяється на реостаті, буде максимальною, коли зовнішній опір дорівнює внутрішньому опору джерела струму.

Питання фізикам: Яке практичне значення має представлена вами задача?

Відповідь: Від корисної потужності напряму залежить коефіцієнт корисної дії джерела струму, а це має важливе практичне значення для економного споживання електричної енергії.

Секретар: Дякуємо представникам кафедри фізики за важливі кроки до енергетичної незалежності. Хто б міг подумати, що ефективність лікування також можна прорахувати. Переконатись в цьому нам допоможуть наші майбутні медичні робітники. (слайд «Кафедра медицини»)

Задача 6. Концентрація ліків у крові хворого через деякий час після ін’єкції задається формулою: 

16t

                                                                                          ₂                            С(t) ^ (10t 20)₂ ,

( t – в секундах )

Знайти       максимальну        концентрацію ліків у крові і час, коли вона досягається.

Розв’язання

Розглянемо дану залежність, як функцію, у якої змінною величиною є час t.

Областю допустимих значень змінної є множина додатних чисел (t > 0).

          Знаходимо похідну даної функції:

                                                          16(10t 20)² 16t2(10t 20)10    16(2010t)

                                        _С(t) _                 (10t     )4                                  _ (10t _20)3 .

20

Прирівнюємо похідну до нуля і знаходимо критичні точки функції.

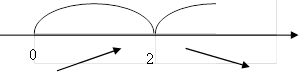
С(t)  0, 16(10(20t ^20¹⁰)^t₃⁾  0, _^1020t_¹⁰20t _ 00,, t  2(c). Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

t

                                                                                                        (max)                                   

Отже, через 2с після ін’єкції концентрація ліків в крові хворого буде

максимальною і дорівнюватиме:     С(2)    0,⁰².

Питання медикам: Як саме використовуються отримані вами результати?

Відповідь: Отримані нами результати використовуються при розрахунках дози препаратів для ефективного лікування і визначення часу, коли цей ефект буде максимальним.

Секретар: Дякуємо представникам кафедри медицини, а тепер просимо представників кафедри будівництва та архітектури переконати нас в можливості заощадити кошти на будівництві і не сумніватись в безпечності конструкцій. (слайд «Кафедра будівництва та архітектури»)

Задача 7. До нас звернувся мешканець нашого міста, у якого вистачає грошей тільки на закладку цоколю довжиною 60м з однією перегородкою. При цьому він бажає, щоб площа будинку була найбільшою. За цими вимогами ми склали задачу і розв’язали її.

 

Розв’язання

     Схема цоколю представляє собою прямокутник з перегородкою, периметр якого дорівнює: Р=3х+2у=60. 

Змінними величинами є ширина х (в тому числі і перегородка) і довжина у, які змінюються в межах: 0<х<20, 0<у<30.

                                                                                                                                   Щоб перейти до однієї змінної,

                                                                                                                                     Р  3х    60  3х

виразимо довжину через ширину і периметр: у                           .

                                                                                                                                            2             2

         Площа будинку задається формулою:

S  x y, S(x)  x(603х)  30x  3x2 .

                                                                                                                              2                     2

Знаходимо похідну даної функції:

S(x)  303х  3(10 х) .

Після спрощення прирівнюємо похідну до нуля і знаходимо критичні точки функції.

                                         S(x)  0,  3(10 x)  0,   x 10(м),    у   15(м).

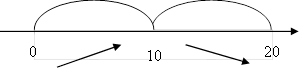
Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

x

                                                                                             (max)                                    

 Отже, площа будинку буде максимальною, коли ширина (в тому числі і перегородка) будинку становитиме 10м, а довжина 15м.

Питання архітекторам: Яку користь отримає ваш замовник?

 Відповідь: Наш замовник залишився задоволеним результатами наших розрахунків, оскільки саме такий проект дасть йому можливість при максимальній корисній площі зекономити на будівельних матеріалах при зведенні стін.

Задача 8. З колоди радіусу R треба виготовити балку прямокутного перерізу. Яке відношення розмірів цього перерізу забезпечить найбільшу міцність балки?  Розв’язання

     В перерізі колоди балка представляє собою прямокутник, вписаний в коло.

Його розміри, ширина х, довжина у і

діаметр колоди 2R (діагональ прямокутника), зв’язані між собою теоремою

Піфагора. Ширина і довжина балки є змінними величинами. Області допустимих значень змінних є: 0<x<2R,  0<y<2R. 

Щоб перейти до однієї змінної, виразимо довжину через ширину і радіус колоди за наслідком з теореми Піфагора: ^у2  4R²  x² .

         Міцність даної балки задається формулою: 

Р(х)  kх(4R²  x²)  4kR²хkx³, де k – коефіцієнт, який залежить від матеріалу колоди.

Знаходимо похідну даної функції: Р(х)  4kR² 3kx²  k(4R² 3x²) .

Прирівнюємо похідну до нуля і знаходимо критичні точки функції.

                                                                                  ²                3x²  0, х²  4R² , х₁  2R, х₂   2R.

Р(х)  0,                                   4R  3        3        3

Від’ємне значення змінної не задовольняє ОДЗ.

Далі позначаємо критичну точку на ОДЗ і визначаємо знаки похідної:

 

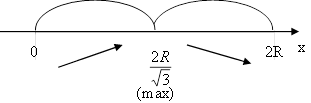
         Знаходимо відповідне значення довжини прямокутника: 

 ,

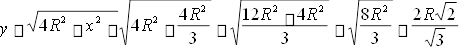тоді відношення довжини до ширини становитиме:

у 2R 2 2R 2R 2 3 7      2 1,4   . х 3 3 3 2R 5

Питання архітекторам: Чи застосовуються результати ваших досліджень на практиці?

Відповідь: Так, саме таке відношення розмірів перерізу балки застосовується, як відомо, будівельниками в реальних умовах. 

Секретар: Дякуємо представникам кафедри будівництва та архітектури. І, нарешті, слово надається гуманітаріям для відкриття літературної сторінки «Прислів’я про навчання різними мовами». (слайд «Кафедра іноземної філології») Після складних досліджень настав слушний момент перевести подих перед наступним етапом нашої роботи.

Як стверджувала перша наша жінка математик С.В.Ковалевська: «Математик повинен бути поетом в душі».

 

Приклади:

•      Live and learn (Живи и учись ); 

Man lernt, solange man lebt (Человек учится, пока живёт); 

Lernen ist nie zu spät (Учиться никогда не поздно);

Вік живи — вік учись.

•      Не who makes no mistakes, makes nothing (Кто не ошибается, тот ничего не делает);

Der Untätige macht keine Fehler (Не ошибается тот, кто ничего не делает);

Durch Schaden wird man klug (На ошибках учатся);

 Не помиляється той, хто нічого не робить.

•      Не that would eat the fruit must climb the tree (Тот, кто любит фрукты, должен влезть на дерево, чтобы их сорвать); 

Ohne Fleiss kein Preis (Без усердия не будет и награды);

Без труда не вытащишь и рыбки из пруда;  Любишь кататься, люби и саночки возить;  Без труда нема плода.

•      Better untaught than ill-taught (Лучше быть необученным, чем плохо обученным); 

Недоученный хуже неученого;  Напівзнання гірше  незнання.

•      Учение да труд к славе ведут.

•      Гарно того навчати, хто хоче все знати.

•      Знання людині — що крила пташині.

 Секретар: Дякуємо представникам кафедри іноземної філології. А зараз слова просять представники преси, у них є для нас важливе повідомлення.

 Представники преси: Під час нашої конференції, яка транслюється у прямому ефірі, до нас надійшло дуже багато питань від слухачів. Ми вибрали два найактуальніших з них і пропонуємо вам, молодим науковцям, допомогти у вирішенні цих нагальних проблем. Найкращі пропозиції ми відправимо нашим респондентам. (слайди «Питання від слухачів»)

Питання від слухачів:

1.     В якому віці корови  будуть приносити найбільшу кількість молока на добу, якщо її приблизно можна описати функцією:

У(х) = –9,3 + 6,86х – 0,49х² , де х – вік корови в роках (2<х<20),  

У – кількість молока в літрах. Якою буде ця кількість?

2.     При якій швидкості легкового автомобіля витрати пального будуть найменшими, якщо їх приблизно можна описати функцією:

У(х) = 0,0017х² – 0,18х + 10,2, де х – швидкість автомобіля в км/год. (30<х<200), У – кількість літрів пального на 100км. Якими будуть ці витрати?

Учні самостійно розв’язують запропоновані задачі. Результати передають секретарю.

4. Підсумок уроку. Рефлексія.

Представники преси: Ми б хотіли запитати науковців, які висновки вони зробили в ході сьогоднішнього засідання?

Представники кафедр відповідають, що в ході конференції вони остаточно переконались в актуальності представлених досліджень, а отже і необхідності вивчення даної теми в навчальних закладах.

Питання вчителю: А як ви оцінили роботу кафедр?

Вчитель: ( вчитель оцінює роботу кожної кафедри, враховуючи критерії оцінювання, в залежності від того: як вони розв’язували задачі, які помилки були допущені, як відповідали представники кафедр на запитання учнів) Заключне слово вчителя

Вчитель: А, загалом, я вважаю, що з поставленою задачею ви впорались: 

-    ви обрали цікаві об’єкти для дослідження;

-    переклали задачі мовою функцій;

-    витримали структуру поетапного розв’язування задач; 

-    продемонстрували вміння застосовувати апарат диференціального обчислення до моделювання реальних життєвих процесів;

-    довели, що вмієте аналізувати, робити висновки, відстоювати свою позицію, використовувати отриману інформацію в особистому житті.

І, наостанок, я хочу подякувати нашим філологам за ту народну мудрість, про яку вони нам нагадали. Мови різні, а мудрість одна: «З усіх скарбів знання найцінніше, тому що воно не може бути ні вкраденим, ні загубленим, ані знищеним».

 Ось така вона – народна мудрість. І я маю надію, що в ході підготовки і проведення нашої конференції ви змогли поповнити свою власну скарбничку.

Секретар: Засідання нашої наукової ради завершено. Пропоную проект рішення:

В ході засідання наукової ради учні переконливо продемонстрували, що вони можуть за умови повної самостійності:

-    обрати об’єкт для дослідження;

-    перевести задачу на мову математики;

-    сформувати математичну модель і розв’язати задачу;

-    знайти і виправити помилки;

-    критично осмислити отриманий результат. 

Отже, можна вважати цілком успішними дії з розширення компетентностей учнів щодо застосування апарату диференціального обчислення до моделювання реальних життєвих процесів і уміння їх оптимізувати.

Домашнє завдання. Скласти і розв’язати свою задачу прикладного змісту.

Урок закінчено. Бажаю всім успіху. Дякую за урок!