Відкрите заняття з математики на тему "Логарифми та їх властивості"
Ознайомити студентів із поняттям логарифма та його властивостями. Узагальнити та систематизувати знання по темі «Логарифми та їх властивості».
План відкритого заняття з математики «Логарифми та їх властивості»
Вид заняття: Лекційно - практичне
Дисципліна: Математика
Група: О,Е11
Спеціальності: 073 «Менеджмент»; 076 «Підприємництво, торгівля та біржова діяльність». Спеціалізація «Організація виробництва», «Економіка та підприємництво».
Тема заняття: Логарифми та їх властивості.
|
Мета заняття: |
Ознайомити студентів із поняттям логарифма та його властивостями. Узагальнити та систематизувати знання по темі «Логарифми та їх властивості». |
|
Розвиваюча: |
Розвивати у студентів впевненість у собі, допомагати у становленні особистості. Розвивати абстрактне мислення, математичну культуру мовлення, вміння аналізувати, систематизувати та узагальнювати факти, робити висновки. |
|
Виховна: |
Виховувати у студентів працелюбність, зібраність, організованість, вимогливість до себе. Сприяти вихованню самостійності студентів, наполегливості у пізнанні нового, уміння чітко формулювати і відстоювати свою думку. |
Мета відкритого заняття:
Показати методику проведення лекційно – практичного заняття з використанням інформаційно-комунікаційних технологій.
Тип заняття: Повідомлення і засвоєння нових знань, формування вмінь та навичок.
Методи: Інформаційно - розвивальні, проблемно – пошукові, творчо - продуктивні.
Матеріально-технічне забезпечення заняття: комп’ютер, мультимедійний проектор, інтерактивна дошка.
Навчальне місце (аудиторія чи лабораторія): аудиторія №216
Література (основна):
1. Бевз Г., Бевз В. «Математика. Алгебра і початки аналізу 11 клас» – Київ: Генеза, 2019 р, розділ 1, §4.
2. Мерзляк А.Г., Номіровський Д.А. «Алгебра 11 клас» – Харків: Гімназія, 2012р., §3, п.21.
3. Істер О., Єргіна О. «Алгебра і початки аналізу 11 клас» – Київ: Генеза, 2019 р., розділ 1, §4.
Література (додаткова):
1. Нелін Є. П. «Алгебра і початки аналізу 10 клас» – Харків: Світ дитинства,
2006 р., розділ 4, §31.
Структура і хід заняття
1. Організаційна частина
Привітання, перевірка наявності і підготовки студентів до заняття.
2. Актуалізація опорних знань студентів і мотивація навчальної діяльності
Запитання до студентів
- Узагальнене поняття степеня та його властивості.
- Поняття кореня п-го степеня та його властивості.
- Показникова функція, її властивості і графік.
- Ірраціональні рівняння.
3. Повідомлення теми, мети, змісту і послідовності вивчення нового матеріалу
Тема заняття: Логарифми та їх властивості.
- Поняття логарифма. Властивості логарифмів.
- Приклади обчислення логарифмів.
4. Узагальнення і систематизація знань і вмінь
Узагальнення і закріплення матеріалу, шляхом перегляду мультимедійних
презентацій на тему «Застосування логарифмів», підготовлених студентами.
5. Підсумки заняття студентів
Підведення підсумків заняття. Аналіз загальної активності студентів, шляхом
рефлексії.
6. Домашнє завдання
1. Мерзляк А.Г., Номіровський Д.А. «Алгебра 11 кл» - Харків: Гімназія, 2012р., частина 2; §3, п.21, №21.22, №21.23
Пояснення нового матеріалу
Поняття логарифма та його властивості
Означення. Логарифмом числа ![]() за основою
за основою ![]() називають показник степеня, до якого треба піднести основу
називають показник степеня, до якого треба піднести основу ![]() , щоб отримати число
, щоб отримати число ![]() , і позначають
, і позначають ![]() .
.
Означення. Логарифмом числа ![]() за основою
за основою ![]() називають натуральним логарифмом і позначають
називають натуральним логарифмом і позначають ![]() .
.
Той факт, що число х є логарифмом числа ![]() за основою
за основою ![]() записують так:
записують так: ![]()
Якщо ![]() і
і ![]() ,
, ![]() , то степінь
, то степінь ![]() існує при довільному дійсному значенню
існує при довільному дійсному значенню ![]() .
.
Наприклад з рівності ![]() випливає, що
випливає, що ![]()
Завдання 1. Записати у вигляді логарифма
1) ![]() ;
; ![]() ;
;
2) 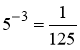 ;
; 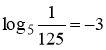 ;
;
3) ![]() ;
;  .
.
Завдання 2. Знайти таке число х, логарифм якого:
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() .
.
Завдання 3. Обчислити 1) ; 2)
; 2) ![]()
1) 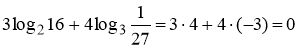 ;
;
2) ![]()
Основна логарифмічна тотожність ![]()
Наприклад ![]() ,
, ![]() ;
; ![]() .
.
Основні властивості логарифмів
Теорема 1. Логарифм добутку двох додатних множників дорівнює сумі їх логарифмів
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Теорема 2. Логарифм частки двох додатних чисел дорівнює різниці логарифмів діленого і дільника
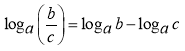 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Теорема 3. Логарифм степеня додатного числа дорівнює показнику степеня, помноженому на логарифм основи цього степеня
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Теорема 4. Логарифм кореня додатного числа дорівнює логарифму підкореневого виразу , поділеному на показник кореня
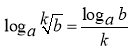 ,
, ![]() ,
, ![]() ,
, ![]() .
.
Теорема 5. Якщо логарифми двох додатних чисел за тією самою основою рівні, то й самі числа рівні. І навпаки, якщо два додатні числа рівні, то і їх логарифми за тією самою основою рівні.
До основних властивостей логарифмів належать ще й такі:
1. ![]() ;
;
2. ![]() ;
;
3. 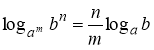 ,
, ![]() ;
;
4. ![]() ;
;
5. 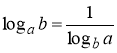 ;
;
6. 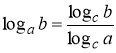 ,
, ![]() ; формула переходу до іншої основи, множник
; формула переходу до іншої основи, множник 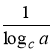 називають модулем переходу.
називають модулем переходу.
7. Якщо ![]() , то
, то ![]() ;
;
8. ![]() .
.
Прологарифмувати одночлен означає виразити його логарифми через логарифм додатних чисел, що входять до його складу.
Означення. Перетворення, за допомогою якого за даним логарифмом числа (виразу) визначають саме число ( вираз) називають потенціюванням.
Означення. Функцію, обернену до показникової ![]()
![]() ,
, ![]() ,
, ![]() називають логарифмічною функцією з основою
називають логарифмічною функцією з основою ![]() і позначають
і позначають ![]() .
.
Графік логарифмічної функції ![]() симетричний графіку показникової функції
симетричний графіку показникової функції ![]() ,
, ![]() ,
, ![]() відносно прямої
відносно прямої ![]() .
.
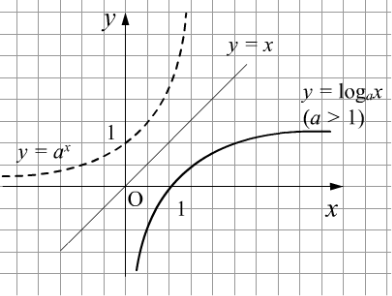
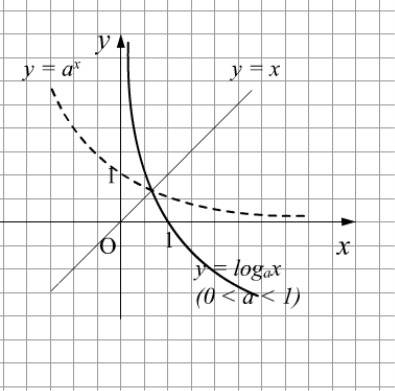
Властивості логарифмічної функції.
-
Область визначення:
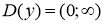 ;
;
-
Область значень
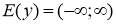
-
Монотонність:
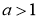 , зростає;
, зростає; 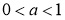 спадає.
спадає.
Властивості логарифмів чисел за основою ![]()
-
Якщо
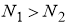 то і
то і 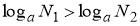 ;
;
- Логарифми чисел, більших за одиницю додатні; логарифми чисел, менших за одиницю , від’ємні.
- Якщо число зростає необмежено, то і логарифм його зростає необмежено; якщо число, залишаючись додатним, прямує до нуля, то логарифм його стає від’ємним і як завгодно великим за модулем.
Властивості логарифмів чисел за основою ![]()
Якщо ![]() то
то ![]() ;
;
- Логарифми чисел, більших за одиницю від’ємні; логарифми чисел, менших за одиницю , додатні.
- Якщо число зростає необмежено, то і логарифм його спадає необмежено; якщо число, залишаючись додатним, прямує до нуля, то його логарифм необмежено зростає
Завдання для самоперевірки
1. Використовуючи знак логарифма, записати показник степеня з рівностей:
1)![]() , (
, ( ![]() )
)
2)![]() (
(![]() )
)
- Обчислити
1)![]() ; 2)
; 2) ![]() , 3)
, 3)![]() ; 4)
; 4)![]()
5)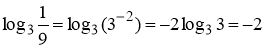 ;
;
6)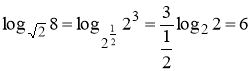
3. Пропотенціювати вираз
1)![]() ;
; ![]() ; 2)
; 2)![]() ;
; 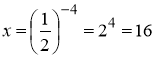 ;
;
3)![]() ;
; ![]() ; 4)
; 4)![]() ;
; ![]() .
.

про публікацію авторської розробки
Додати розробку
