Використання комп’ютерних технологій при вивченні математики

 

 

 

 

 

 

 

 

 

 

 

Використання комп’ютерних технологій при вивченні

математики

 

 

 

 

 

 

 

ЗМІСТ.

Вступ……………………………………………………………………….3

Розділ І. Передумови застосування інформаційних технологій при               вивченні матема­тики………………………………………………………4

Розділ ІІ. Загальна характеристика комп'ютерних програм по лінії            застосування при вивченні курсу математики.

1. Передумови застосування інформаційних техноло­гій при вивченні математики……………………………………………..6
2.  Загальна характеристика комп'ютер­них програм  по лінії  застосування при вивченні  курсу математики…………………….6

Розділ ІІІ. Дослідження тем алгебри і початків аналізу, геометрії на          необхідність за­стосування інформаційних технологій.

1. Алгебра та початки аналізу………………………………….… 11

               3.2 Геометрія………………………………………………….……. 11

Розділ IV. Викорис­танням  програмних засобів на уроках математики                 ( із досвіду роботи)………………………………………………………….. 14

       4.1 Робота з програмами GRAN1, GRAN-2D, GRAN-3D……….    14

                 4.2 Робота з програмою ADVANCED GRAPHER 2 ……………   19

 

Розділ V. Використання презентацій  на уроках математики….……....37

Висновки……………………………………………………….……..……. 42

Література………………………………………………………………..….44

 

 

 

 

 

 

 

 

 

ВСТУП

 

У сучасному світі мабуть немає галузі, де б не використовувався комп’ютер і освітня галузь не є виключенням. Інтерес до вивчення предмету багато в чому залежить від того, як проходять уроки. Застосування комп'ютерної техніки на уроках дозволяє зробити урок нетрадиційним, яскравим, насиченим, наповнюючи його зміст знаннями з інших наочних областей, що перетворюють математику з об'єкту вивчення в засіб отримання нових знань.

Ефективність застосування нових інформаційних технологій на уроках математики обумовлена наступними факторами:

1)    різноманітність форм представлення інформації;

2)    висока степінь наочності;

3)  можливість моделювання за допомогою комп’ютера різноманітних об’єктів і процесів;

4)  звільнення від рутинної роботи, що відвертає увагу від  засвоєння основного змісту;

5)  можливість організації колективної та індивідуальної  дослідницької роботи;

6)  можливість диференціювати роботу учнів у залежності від рівня підготовки, пізнавальних інтересів та ін.; використовуючисучасні інформаційні технології;

7)  можливість організувати комп’ютерний оперативний контроль і допомогу з боку вчителя;

8)  можливості комп’ютера дозволяють учню активно приймати  участь у процесі пізнання.

 

 

 

 

РОЗДІЛ I.

ВИКОРИСТАННЯ ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ ПРИ ВИКЛАДАННІ МАТЕМАТИКИ – ФАКТОР ПІДВИЩЕННЯ ФУНДАМЕНТАЛЬНОСТІ МАТЕМАТИЧНОЇ ОСВІТИ І РОЗВИТКУ  ТВОРЧОГО ПОТЕНЦІАЛУ УЧНІВ

 

Актуальність теми обумовлена необхідністю удосконалення системи викорис­тання у навчальному процесі комп'ютерних технологій за умов розбудови націона­льної системи освіти, зростання ролі, яку відіграють в інформаційному суспільстві інформаційні технології. Сьогодні у всьому світі відбуваються процеси переходу до інформаційного су­спільства. Україна не стала винятком. Створення телекомунікаційної інфраструктури., забезпечення закладів освіти комп'ютерною технікою, впровадження комп'ютерних програм навчання є невід'ємною частиною реалізації загальнонаціональної програми інформатизації навчального процесу. І якщо наша держава зорієнтована на побудову відкритого суспільства, на інтеграцію у світове співтовариство, то стимулом у розви­тку інформаційних технологій може бути їх впровадження саме у галузь освіти.

Успішна реалізація основних принципів і завдань реформування освіти немож­лива без широкої інформатизації процесу навчання. При цьому пріоритетними на­прямами стають: розробка нових моделей освіти, поступове інтегрування в міжнаро­дну систему освіти; оновлення змісту освіти, створення нової системи методичного забезпечення закладів освіти, їх входження в міжнародну систему комп'ютерної ін­формації; організація навчання як не дискретного, а перманентного процесу науково-методичної та практичної діяльності з використанням нових інформаційних техноло­гій навчання.

Розвиток інформаційних технологій надає великі можливості для підвищення кваліфікаційного рівня вчителів та їхньої культури. І особливого значення при цьому набуває широке поширення мережі Інтернет. Використання всесвітніх інформацій­них ресурсів, що стають доступними завдяки Інтернету, визначає істотний вплив на процеси освіти та пізнання.

Доступ до глобальної мережі в освіті - це нові можливості, як для вчителів, так і для учнів. Інтернет у навчальних закладах може бути використаний не лише для отримання інформації з авторитетних світових джерел, а для організації навчання, проведення Інтернет-олімпіад, конференцій, семінарів. Інформатизація сфери освіти є складовою частиною запровадження нових технологій у суспільстві. Перш за все важливо запроваджувати їх саме в цю галузь, реформування якої зумовлює навчання на прогресивній та оперативній основі. Саме сьогодні учні шкіл будуть розвивати інформаційні мережі XXI століття та „завойовувати" Інтернет-простір.

Оновлення філософії та зміна парадигми освіти в Україні, що фіксуються Зако­ном України “Про освіту” та Законом України "Про загальну середню освіту", Кон­цептуальними ідеями Національної доктрини освіти в Україні, концепцією загальної середньої освіти,  Концепція Державної цільової соціальної програми підвищення якості шкільної природничо-математичної освіти на період до 2015 року; та наявними потребами суспільства щодо готовності реалізувати но­ві підходи до навчання. Сьогодення від учителя вимагає не стільки вміння передава­ти суму знань, скільки підготувати учня до активної самоосвітньої діяльності, активі­зувати саморегулюючі механізми розвитку особистості, сприяти само актуалізації учня, розвивати інтелектуально-творчі здібності, навчити використовувати комп'ютерні технології при вивченні математики.

 

 

 

 

 

 

РОЗДІЛ II.

ОСНОВНА ЧАСТИНА

2.1 Передумови застосування інформаційних техноло­гій при вивченні математики

Сьогодні, коли навколо йде безперервна комп'ютеризація, ми захоплюємося красою і багатством створеного Людиною-Творцем Комп'ютерного Всесвіту. Чотирнадцять – п'ятнадцять років тому ніхто навіть не припускав, що нинішнє покоління буде черпати знання не тільки з паперових підручників, але й зі сріблястих компакт-дисків. Комп'ютер до­зволяє не тільки вирішити складну математичну задачу, зіграти в шахи, але і ство­рювати власну дивну музику, створювати самого себе.

Зміни, що несе із собою інформаційне століття, вимагають від усіх здатності зазирнути в майбутнє і поставити питання, які можна внести зміни у свою діяль­ність, у діяльність школи, щоб гідно вижити в умовах української дійсності^. Україні як ніколи необхідні грамотні, освічені люди, що постійно підвищують свій творчий потенціал, що вміють працювати з інформаційними технологіями. Мета даної роботи  - створення комп'ютерного практикуму з математики для учнів 10-11 класів. Практикум створений для розвитку творчих здібностей учнів, підвищення комп'ютерної грамотності і фундаментальності математичної освіти.

2.2 Загальна характеристика комп'ютер­них програм  по лінії  застосування при вивченні  курсу математики.

 Комп'ютерні математичні системи дозволяють швидко й ефективно проводити обчислення, розв'язувати задачі з алгебри, геометрії, математичного аналізу, статис­тики (знаходити межі, диференціювати, інтегрувати, будувати графіки, діаграми, зо­бражувати стереометричні фігури). Грамотне застосування комп'ютерних техноло­гій у навчальному процесі:

•       підвищує фундаментальність математичної освіти;
•       викликає інтерес до вивчення математики;
•       підвищує комп'ютерну грамотність;
•       стимулює розвиток дитячої творчості;

• сприяє інтеграції освітньої системи з освітніми системами найбільш роз­винених країн світу, де подібні методи навчання вже застосовуються;

•       дає можливість брати участь у міжнародних, дистанційних проектах.

Банк комп'ютерних програм у школі може складатися з наступних програм.Microsoft Word 2007, Microsoft Excel 2003, Microsoft PowerPoint, Gran2D, Gran3D, Paint, Advanced Grapher, Functor-2.5, 3D-Grapher, 3DS max 5.0, «Курсматематики-2000», KoMnac-3D LT 5.10, Mathematics Encyclopedia, Coreldraw,  Adobe Photoshop, Mathematics Encyclopedia.

А) Комп'ютерна програма Advanced Grapher (Автор Michael Serpik)

Унікальна програма для застосування при вивченні шкільного курсу математики. Дозволяє на одній координатній площині зображувати:

•                                              графіки функцій f(x), f(x+a), f(x-a) a>0
•                                              графіки функцій f(x), f(x)+b, f(x)-bb>0
•                                              графіки функцій f(kx+b)+c, |f(kx+b)+c|, f(|kx+b|)+c
•                                              графік y=f(x),, одночасно визначити похідну і побудувати графік похідної;
•                                              рішення систем рівнянь і нерівностей основного і поглибленого рівнів.

Комп'ютерна програма дозволить учням вирішувати дослідницькі завдання: на ви­значення увігнутості, опуклості кривих, у побудові дотичної і нормалі в будь-якій точки області визначення функції, дослідження точок максимуму і мінімуму, найбі­льшого і найменшого значень на проміжку, визначення площі фігури, обмеженої лініям

Б) Комп'ютерна програма 3DSmax 5.0

Популярна програма тривимірної комп'ютерної графіки та анімації. Дана про­грама займається побудовою всіляких моделей (вид яких: стандартні примітиви, складені об'єкти, розширені примітиви, що коректують сітки, системи часток, не­стандартні поверхні, динамічні об'єкти), дає можливість побачити дане геометричне тіло з різних позицій: у перспективі, зверху, спереду, ліворуч. Однією з можливос­тей 3DSmax 5.0 є побудова опуклих багатогранників, до яких належать: тетраедр, ок­таедр, додекаедр. Дуже цікавою особливістю програми є зміна параметрів сімейства гедри: тетра, куб, октаедр, зірка1, зірка2.

В) Комп'ютерна програма Gran

Українська програма Gran призначена для графічного аналізу функцій. Основні фу­нкціональні можливості програми: побудова графіків функцій, обчислення значень виражень функції в заданих точках, графічне розв'язання рішення рівнянь, систем рівнянь, нерівностей і систем нерівностей. Також програма дозволяє обчислювати об'єми і площі тіл обертання. Використання програми дає можливість значно інтен­сифікувати процес навчання.

Програма Gran 3D призначена для побудови базових просторових об'єктів у триви­мірному просторі і їхньому детальному аналізі. Відмінною рисою є можливість обе­ртання просторового геометричного тіла за рахунок пересування повзунків (горизо­нтального і вертикального). Програма дає повну характеристику об'єкта: точки мак­симуму, точки мінімуму, об'єм, площа поверхні, кількість вершин. У резерв програ­ми входить можливість побудови усічених моделей (при натисканні на кнопку «Створення базових об'єктів» з'являється діалогове вікно, у якому необхідно поста­вити значок біля слова «усічений», а також указати параметри верхньої підстави).

Отже, можливості української програмиGran3Dдосить великі: проектування на одну з 3 осей координат, збільшення або зменшення фігури, можливість виконувати над об'єктом різноманітні операції.

Г) Комп'ютерна програма Functor-2.5

Програма для побудови графіків тривимірних функцій і їхнього детального аналізу, зміни настроювання виду графіків і систем координат. Відмінною рисою є можливість обертання просторової моделі одним рухом миші. Робота з програмою представляє необмежені можливості для розвитку просторового мислення учнів.

Д) Комп'ютерна програма «Курс  математики-2000 »» (Автор Л.Я.Боревский)

Теми: Тригонометричні, показові, логарифмічні тотожності, рівняння, нерівності. Кожна програма "Курсу математики" забезпечена гіпертекстовим підручником, у якому будь-яка формула або теорема обов'язково проводиться з доказом, а також ілюструється малюнком або прикладами, що дозволяє застосовувати при формуван­ні нових знань і способів дій, а також при актуалізації попередніх знань. Учню пропонується новий спосіб розв’язання задач: на екрані комп'ютера, разом з комп'ютером, використовуючи комп'ютер як терплячого наставника, що проконтро­лює дії учня, підкаже при необхідності вірний шлях розв'язування і дасть теоретич­ну довідку. Для кожного учня програма веде окремий щоденник з повною статисти­кою по всіх задачах, що розв'язувалися, що дозволяє легко визначити теми, що ви­магають додаткового опрацювання. Диск містить 450 задач для самостійного рішен­ня.

Е) Комп'ютерна програма 3DGrapher

Комп'ютерна програма дозволяє зробити побудову поверхні однієї і тієї ж функції  в декартових, циліндричних і сферичних координатах. Виділити кольором. Порівня­ти зображення. Функції задаються в параметричному виді. Наприклад: x(u,v,t)=uy(u,v,t)=v; z(u,v,t)=. Також є можливість одночасної ілюстрації всіх трьохвидів поверхонь.

Є) Комп'ютерна програма Компас-3DLT 5.10

Програма застосовується при вивченні курсу креслення, але може бути застосовані при вивченні стереометрії (зображення фігур у тривимірному просторі, побудова їх ніх перетинів). Також програма дозволяє обчислювати об'єми і площі тіл обертання Використання програми дає можливість значно інтенсифікувати процес навчання.

Ж) Комп'ютерні програми Word2003, Word2007, Excel, Power Point, Paint, Corel Draw, Adobe Photoshop

Програми можна застосовувати при:

•       складанні учнями коротких і повних конспектів тем (Word);
• побудові найрізноманітніших діаграм і гістограм, обчислень довжин, площ, об'ємів геометричних об'єктів (Microsoft Excel);
• виконанні творчих презентацій з окремих тем, а також навчальних презентацій для вивчення теми математики або для навчання у визначеній програмі (Місгоsoft Power Point);
• створення, зберігання і змінювання  на комп’ютері різних зображень (малюнків,  креслень, мультиплікацій) (Corel Draw,  Adobe Photoshop).

З) Комп'ютерна програма Corel Draw

 Corel Draw - векторний  графічний  редактор. За допомогою векторної  графіки  можна легко й швидко малювати  об’єкти  простої геометричної форми. У векторному способі кодування геометричні фігури, криві й прямі лінії, що складають малюнок, зберігається в пам’яті комп’ютера у вигляді  математичних формул і геометричних абстракцій – круг, квадрат, еліпс тощо. За допомогою математичних формул  можна описати  найрізноманітніші фігури.

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ ІІІ.

ДОСЛІДЖЕННЯ ТЕМ АЛГЕБРИ І ПОЧАТКІВ АНАЛІЗУ, ГЕОМЕТРІЇ НА НЕОБХІДНІСТЬ ЗАСТОСУВАННЯ ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ

3.1 Алгебра і початки аналізу

     Тема Похідна. Застосування похідної (використання програм Advanced Grapher, Gran).

• побудова графіка функції і графіка її похідної на одній координатній пло­щині на екрані комп'ютера. Дослідження залежності проміжків зростання, спадання функції від знака похідної ;
• зображення графіка функції, дотичної і нормалі в даній точці. Обгрунту­вання геометричного змісту похідної;
• побудова графіка функції і графіка другої похідної. Дослідження функції на увігнутість і опуклість у залежності від знака другої похідної;
• проведення повного аналітичного дослідження функції за допомогою похідної, побудова графіка функції в зошиті з наступним порівнянням його на екрані комп'ютера;
• дослідження точок максимуму, мінімуму, перегину на зміну знака в межах цих точок.

Тема Первісна й інтеграл (використання програм:Advanced Grapher, Gran )

• зображення й обчислення площі фігури, обмеженої лініями аналітично і за допомогою комп'ютера ;
•       обчислення визначеного інтеграла;
•       дослідження завдань, що приводять до поняття інтеграла;
• геометричний зміст загального вигляду первісної для показникової, лога­рифмічної та степеневої функцій;
•       формула Ньютона-Лейбніца. Геометричний зміст.

 

Тема Тригонометричні, логарифмічні і показові функції (використання програм Advanced Grapher, Gran, Functor-2.5, 3D-Grapher)

-   побудова графіків функцій y=f(x), y=f(x+a), y=f(x-a) a>0;

 -     графіків функцій y=f(x), y=f(x)+b, y=f(x)-bb>0;

• графіків функцій y=f(kx+b)+c, y=|f(kx+b)+c|, y=f(|kx+b|)+c. Провести до­
  слідження виду графіків у залежності від коефіцієнтів а, Ь, с і положення
  модуля. Обґрунтувати висновки.

Тема Тригонометричні, логарифмічні і показникові

рівняння, нерівності і системи

(використання програм «Курс математики-2000», Advanced Grapher,

Gran)

• графічне розв'язання нерівностей і систем нерівностей. Обґрунтування
  виду зображення на екрані комп'ютера;
• розв'язання дослідницьких завдань з комп'ютерної програми  «Курс
  математики-2000»;
•      дослідження параметричних рівнянь.

 

3.2 Геометрія

Тема Багатогранники і круглі тіла

(використання програм Microsoft Word 2007, Microsoft Excel 2003, Microsoft PowerPoint, Gran3D, Paint, 3DS max 5.0, KoMtiac-3D LT 5.10)

   З огляду на властивості проектування виконати:

•       зображення стереометричних фігур;
•       зображення перетинів багатогранників;
•       зображення комбінацій багатогранників;
•       зображення опуклих, зірчастих багатогранників.

Обчислити: довжини, площі, обсяги геометричних об'єктів.

Тема Декартові координати в просторі

                   (використання програмFunctor-2.5, 3D-Grapher)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ IV.  

Викорис­танням  програмних засобів на уроках математики

( із досвіду роботи)

4.1  Робота з програмами GRAN1, GRAN-2D, GRAN-3D.

Працюючи на протязі багатьох років в профільних класах та враховуючи, що сьогодні темп розвитку  суспільства надзвичайно високий, звичайно, переконуєшся,  що треба встигати за змінами.  Варто переробляти величезні масиви інформації, яка надходить з усіх точок земної кулі, відкривати широкі перспективи щодо гуманітаризації освіти  і гуманізації навчального процесу.  Це неможливо без поглиблення та розширення теоретичної бази знань і надання результатам практичного значення. Особливу роль слід відводити активізації пізнавальної діяльності, створенню умов для повного розкриття творчого потенціалу з урахуванням їхніх вікових  особливостей і життєвого досвіду, індивідуальних нахилів дітей, їх запитів і здібностей. Не можна  не прийти  до висновку, що на уроках математики потрібно  більш широко застосовувати програмні засоби, що дозволяють розв’язувати за допомогою комп’ютера досить  широке коло математичних задач різних рівнів  складності.

         Тому на уроках в класах, фізико – математичного та природничого профілів, я дуже часто використовую  такі програмні засоби навчання:  GRAN1, GRAN-2D, GRAN-3D.

         Ці програмні засоби  стали моїми помічниками при розгляді багатьох тем, як з алгебри, так із геометрії.

    Завдяки можливостям графічного супроводу комп’ютерного розв’язування задачі, учень чітко і легко розв’язує досить складні задачі, впевнено володіє відповідною системою понять і правил. Використання подібних програм дає можливість  у багатьох випадках зробити розв’язування задач настільки ж доступним, як і просте розглядання малюнків чи графічних зображень.

          Такий підхід до вивчення математики дає наочні уявлення про поняття, що вивчаються, розвиває образне мислення, просторову уяву,  дозволяє досить глибоко проникнути в сутність досліджуваного явища, неформально розв’язувати  задачу.

          Відповідні програми перетворюють окремі розділи і методи математики в «математику для всіх», що робить  їх доступними, зрозумілими, легкими і зручними для використання.

           Наведу приклад із свого досвіду, про використання мною   програмних засобів навчання  при вивченні теми:

ОБЧИСЛЕННЯ ВИЗНАЧЕНИХ ІНТЕГРАЛІВ

Програмне забезпечення GRAN-2D

1. Послуга Обчислення /Інтеграл

Для обчислення значень визначених інтегралів виду f(x)dx від неперервних на проміжку функцій виду y=f(x) призначено послугу Обчислення /Інтеграл.  На вкладниці Інтеграл  вікна  Обчислення, що з’явиться, у полі біля напису f(x)=  необхідно ввести вираз підінтегральної функції, а у полях  біля написів а= та в=  вказати значення нижньої та верхньої меж інтегрування. Після введення даних для виконання обчислення  необхідно натиснути кнопку  Обчислити, після чого результат буде виведено у поле Результат обчислення.

   Інтеграл обчислюється наближено за методом трапецій, що полягає в заміні графіка залежностіy=f(x) ламаною лінією  над відрізком. При цьому відрізокділиться на n частин, після чого наближено покладається

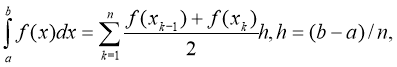   х_o=а,    х_n=b,  x_k= х_o+kh.

  Кількість точок поділу інтегрування (n) можна задати  при налагодженні програми.

 

Приклад №1

Обчислити площу фігури, обмеженої лініями х=0, х=10,у=0 у=хsin(x), тобто обчислити інтеграл.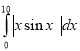

 

РОЗВ’ЯЗУВАННЯ

На вкладинціІнтеграл вікна Обчислення введемо у поле біля запису (х)=  вираз  abs (xsin(x)), а у поля біля написів   a=  та  b= введемо відповідно 0 та 10. Після  натискання кнопки Обчислити  отримаємо результат 29.85230.

Відповідь:  30

Приклад №2

 Обчислити площу поверхні тіла обертання, що утворюється обертанням навколо осі Ох кривої на проміжку від  -  до  .

РОЗВ’ЯЗУВАННЯ

Оскільки площа поверхні, що утворюється обертанням навколо осі  Ох  кривої у= (х) в межах від точки(а(а)) до  (b(b)),обчислюється  за формулою 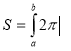(х), то необхідно обчислити інтеграл

2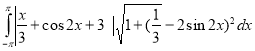. На вкладинці Інтеграл вікна Обчислення введемо  у поле біля напису (х)= вираз

  2abs(x3+cos(2x+3)sqrt(1+(13-2sin(2x))^2) , а у  поля біля написів a= та b=  введемо відповідно - та. Після  натиснення кнопки Обчислити  отримуємо результат 203.3=2Е2.

Відповідь: 203.3

Приклад №3

Обчислити площу фігури, обмеженої лініями х=3, х=3.5, у=0, у=х^1..5, тобто обчислити інтеграл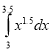

РОЗВ’ЯЗУВАННЯ

На вкладниці Інтеграл вікна Обчислення введемо  у поле біля напису (х)= вираз х^1.5 , а у  поля біля написів a= та b=  введемо відповідно 3 та 3.5. Після  натиснення кнопки Обчислити  отримуємо результат 2.9322.9

Відповідь: 2.9

 

Програмне забезпечення GRAN

Обчислення об’ємів  та площ поверхонь тіл обертання

        Об’єм тіла, обмеженого поверхнею, що утворюється  обертанням лінії, описуваної рівнянням виду у=f(х), навколо осі Ох, і площинами х=а, х=b, можна обчислити також, скориставшись послугою «Інтеграл» для обчислення визначеного інтегралу виду 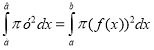, значення якого і буде значенням шуканого об’єму.

        Об’єм тіла, обмеженого поверхнею, що утворюється  обертанням лінії, описуваної рівнянням виду у=f(х), навколо осі Оу, і площинами у=с, у=d, можна обчислити також, скориставшись послугою «Інтеграл» для обчислення визначеного інтегралу виду

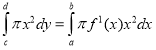, де a і b такі, що f(a)=c, f(b)=d , або 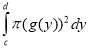, де

g(y)-функція, обернена до f(x).

       Об’єм тіла, що утворюється обертанням навколо осі Оу фігури, обмеженої лініями у=f(х), х=а, х=b, у=0 (приf(х)≥0) можна обчислювати за формулою.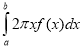

Площа поверхні, що утворюється обертанням навколо осі Ох кривої у=f(х) в межах від точки (а,f(a)) до (b,f(b)), обчислюється за формулою

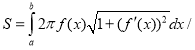
Крива описується рівнянням виду x=, у=, тоді за формулою

.

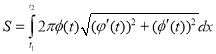Приклад 4.

   Обчислити об’єм тіла, що обмежений поверхнею, утвореною обертанням кривої навколо осі Ох в межах від  х₁ = - 3.14 до  х₂ = 3.14

Алгоритм розв’язування  

1.Побудуємо графік заданої функції:

   Об’єкт /Нова функція/ Вікно «Графік/»  «Введіть вираз»

/Вікно «Графік »/ відрізок визначення А=-3.14; В=3.14/

   Графік/ Побудувати/

    В вікні графік з’явиться графік функції на відрізку.

2.Інтеграли/ Об’єм , вісь Ох/ , вказавши межі інтегрування а=-3.14, b=3.14

         В результаті  одержимо об’єм тіла .

Відповідь:V=195.269559348 куб. од.

Приклад 5

Знайти об’єм зрізаного конуса, утворюваного навколо осі Оу  трапеції, обмеженої лініями  х=0, у=0,у=3, у=4-2х.

Приклад 6

        Знайти об’єм тіла, утвореного обертанням навколо осі  ОУ фігури, обмеженої лініями у=, у=3, у=5, у=4.                                                                           

                            Програмне забезпечення GRAN-3D

В програміGRAN-3D   передбачено обчислення об’ємів та площ поверхонь тіл обертання , твірні яких обертаються навколо осі Ох або Оу у прямокутній Декартовій системі координат та задаються одним із трьох способів:

1.У вигляді явної залежності між змінними х і у:  у=f(х);

2.У вигляді параметрично заданої залежності між змінними х і у:

,,де t- змінна-параметр;

3.У вигляді плоскої ламаної, що задається послідовністю своїх вершин у площині хОу     

Площа поверхні, що утворюється обертанням навколо осі Ох кривої у=f(х) в межах від точки (а,f(a)) до (b,f(b)), обчислюється за формулою

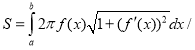, а об’єм, що нею обмежений, за формулою

.

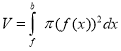Якщо обертання відбувається навколо осі Оу, то формули набувають вигляду

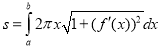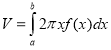,(приf(х)≥0).

Крива описується рівнянням виду x=, у=, тоді за формулою

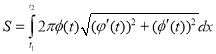,а об’єм 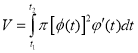, де t_{1 ,}t₂- значення параметра t,що відповідають кінцевим точкам Ата В кривої.

При  обертанні кривої навколо осі Оу площа поверхні тіла обертання та його об’єм обчислюються за формулами

, .

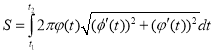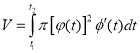4.2 Робота з програмою ADVANCED GRAPHER 2

 

Зручною у використанні і з цілою низкою корисних властивостей є програма Advanced Grapher. За допомогою цієї програми можна будувати графіки функцій, обчислювати значення функцій, проводити дослідження функцій. Вдалим є те, що можна будувати графіки кількох функцій в одній системі координат, змінюючи при цьому колір лінії графіка та її товщину.

Використовуючи готові графіки не важко навчити учнів «зчитувати» властивості відповідних функцій: проміжки монотонності, знакосталості, точки екстремуму, розв’язувати нерівності f(x) <0  (f(x) >0) тощо.

Варто зазначити, що таку роботу доцільно проводити не у мультимедійному, а у комп’ютерному класі, бажано разом із вчителем інформатики, який міг би закріпити та оцінити вміння учнів користуватися можливостями програми Advanced Grapher.

Вирази в ADVANCED GRAPHER складаються із змінних, констант, чисел і функцій від них, з`єднаних операторами.

Оператори

арифметичні оператори: +, -, *, /, ^ (піднесення до степеня).

Приклад: 2+2^3=10

оператори відношення: >,<,>=,<=,=,<>.

Функції

При використанні функцій необхідно використовувати синтаксис <Ім`я функції>(<Аргумент>).

Приклади: sin(x+2); ln(ln(1/x)); sin(x)^3.

Advanced Grapher підтримує слідуючі функції:

Sin - синус cos - косинус tan - тангенс cot - котангенс asin - арксинус acos - арккосинус atan - арктангенс

abs - модуль числа sqrt - квадратний корінь ln - натуральний логарифм lg - десятковий логарифм exp - експонента (exp(x) - e в степені x)

 

 

 

 

 

Константи

У виразах можна  використовувати константу Pi. Якщо ви хочете використати константу e , введіть: exp.

Змінні

Ви також можете використовувати одну або дві змінні, наприклад, X, Y, A або T (в залежності від ситуації).

Додаткова  інформація

Можна пропускати знак множення. Приклади: xy, (x+1)(5y+x), xx, xsin(x).

 

 

Побудова графіків

Advanced Grapher має потужні засоби для управління графіками. Ви можете легко створювати, видаляти, дублювати графіки, змінювати їх властивості та порядок у списку графіків.

Приклад 1

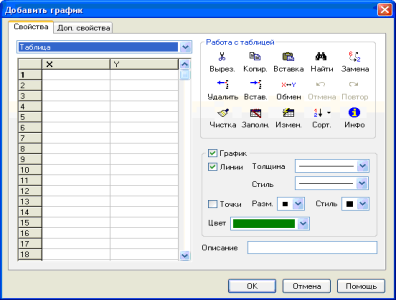
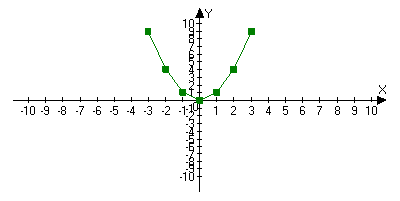
Побудувати графік функції у=х²  по точкам, за допомогою таблиці.

На панелі інструментів натискаємо кнопку «Добавить график», «таблицы». З`являється таблиця, в якій записуємо значення абсцис і ординат графіка. Справа робимо помітку у віконці «точки». Натискаємо ОК.

 

 

 

Приклад 2

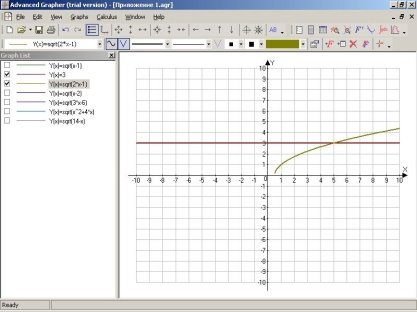
В одній системі координат побудувати графіки функцій у=2х-1 і у=3 і знайти точки їх перетину.

1. Клацніть кнопку на панелі інструментів «График»; або +F. У віконці «Формула» запишіть у=sqrt(2*х-1). Виберіть потрібний колір, товщину і стиль. Натисніть ОК. На екрані з`явиться графік даної функції.

2. Аналогічн побудуйте графік другої функції у=3

3. Клацніть на панелі інструментів «Пересечение» і у віконці У1(х)= введіть першу функцію, а у віконці У2(х)= - другу.

4. Підпишіть назву функції «Правка» - «Добавить метку»

Проставте параметри (межі, в які входять точки перетину).ОК.

На екрані з`явится таблиця, з указаними точками перетину.

Щоб видалити графік – на панелі інструментів натискаємо на віконечко «Удалить графік»

 

 

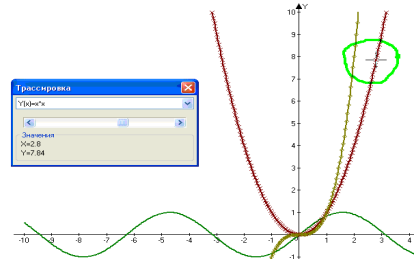
Окремо хочеться виділити можливість відображати ділянку графіка, а також функцію трасировки – можливості візуально переглянути процес побудови графіка переміщуючи повзунок у відповідному діалоговому вікні, там і відображається і значення функції у цій точці. Також хочу відзначити можливість обчислення визначеного інтеграла з функцією визначення як числового значення, так і отримання області, що інтегрується (по якій визначається площа). Також в цій програмі, на відміну від всіх мною переглянутих, є можливість перемикання осі х у тригонометричний вид, тобто кратний pі. Також програма більш коректно обробляє екстремум – не з’єднує протилежні кінці функцій.

 

 

 

Розв`язування рівнянь

За допомогою програми Advanced Grapher зручно роз`язувати рівняння і системи рівнянь.

Відомо, що рівняння іноді простіше розв`язати графічно ніж алгебраїчно. Для цього необхідно побудувати графік функції розміщений в лівій частині рівняння, а потім в правій. Абсциси точок перетину будуть розв`язком даного рівняння.

Приклад 3

Розв`язати рівняння: x³=

Побудуємо графіки функцій: y=x³ і y= і знайдемо точки їх перетину. (Алгоритм побудови графіків функцій і знаходження точок їх перетину дивись у  Прикладі 2.)

 

 

 

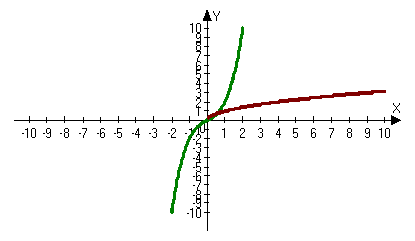
Для розв`язування систем рівнянь треба з кожного рівняння виразити  у  і потім уже будувати графіки. Наприклад, щоб побудувати коло  x<sup>2</sup>+y<sup>2</sup>=25, виражаємо у:  у= - і у=та будуємо два півкола. Приклад уроку з розв`язанням систем рівнянь наведено нижче.

 

Розв`язування нерівностей

При розв`язуванні лінійних нерівностей за допомогою програми Advanced Grapher учні бачать графічну інтерпритацію розв`язку. Вираз набуває від`ємних значень, якщо графік функції записаний зліва знаходиться нижче осі ОХ.

Приклад 4

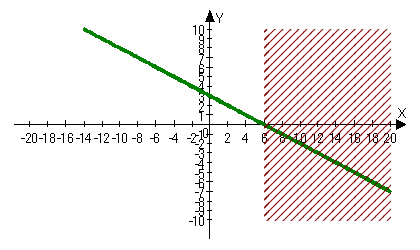
Розв`язати нерівність: 7-0,5х<0.

1. на панелі інструментів натискаємо +F і вводимо функцію у=7-0,5х.
2. клацаємо у першому віконці, шукаємо запис «уравнение или неравенство» і натискаємо ліву кнопку миші. У другому віконці вводимо нерівність і ОК.
3. на екрані з`явиться малюнок

 

 

Приклад 5

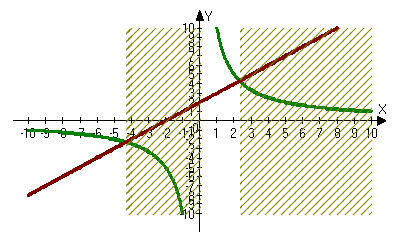
Розв`язати нерівність 10/х<х+2.

Для розв`язання за допомогою програми будують графік функції зліва, потім - функції справа. Оскільки програма може розв`язувати тільки нерівності виду <,>0, то на третьому кроці треба всі доданки перенести вліво і записати у віконці таку нерівність:10/х-х-2<0, (дивись приклад 4).

Розглядаючи малюнок, учням слід пояснити, чому заштриховані саме ці області. Комп`ютер робить штрихи на тих проміжках, де графік функції у=х+2 знаходиться вище графіка функції у=10/х.

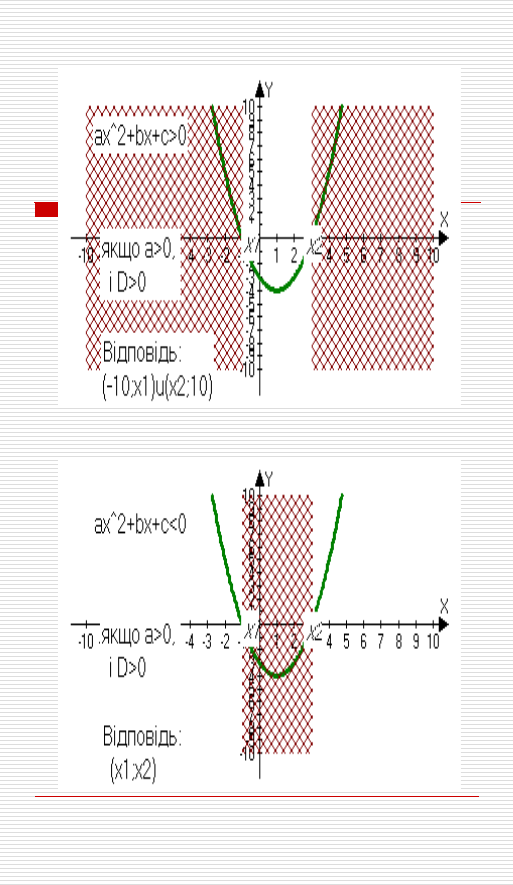
Ця програма – гарний інструмент в руках вчителя при вивченні теми «квадратичні нерівності» графічним способом. Ми знаємо, що кількість розв`язків нерівності залежить від розміщення параболи в системі координат і знаку нерівності. А таких можливостей є велика кількість. Тому на першому уроці можна використати інтерактивну дошку чи комп`ютерний клас для показу презентації, яку швидко і легко зробити за допомогою програми Advanced Grapher.

Щоб активізувати пізнавальну діяльність учнів, їх можна залучити до цієї роботи (попередньо проконсультувавши їх щодо вимог).

 

Прилад можливої презентації:

 

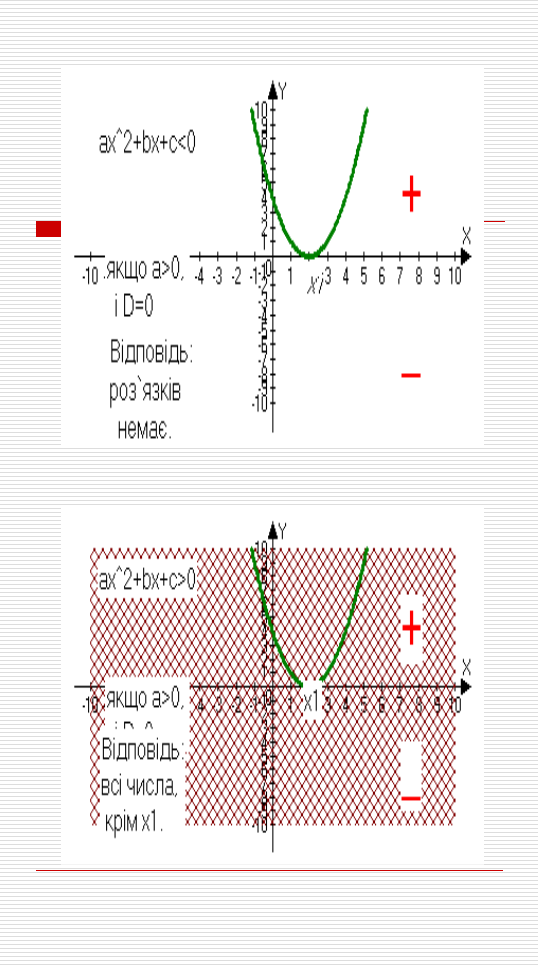
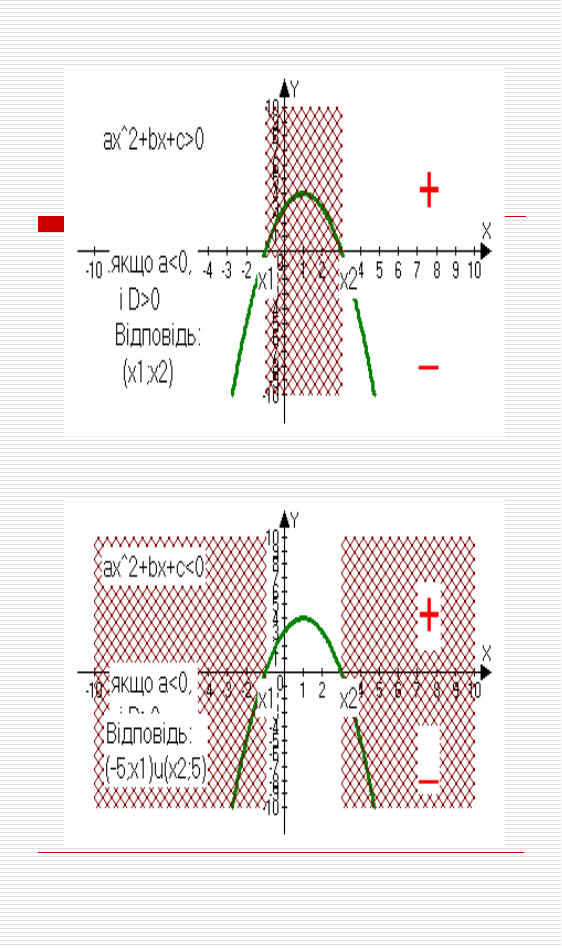
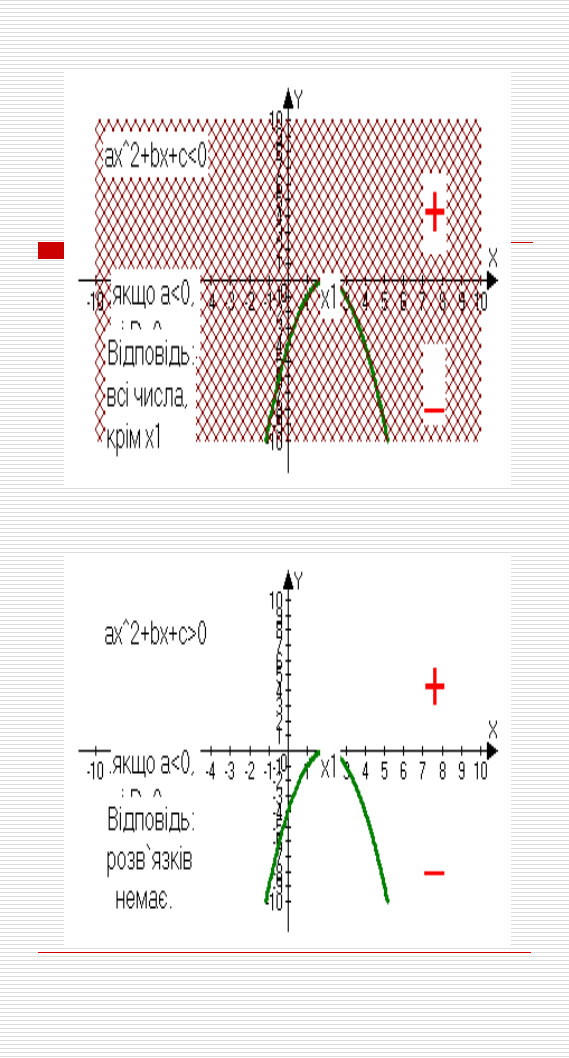
Перетворення графіків функцій

Ця тема зустрічається у шкільному курсі декілька разів. А саме після вивчення квадратичних функцій, а потім тригонометричних. При перетворенні квадратичних функцій, учні для економії часу користуються лекалами. Для перетворення ж тригонометричних функцій у пригоді стає програма Advanced Grapher. При побудові великої кількості графіків учні легко розуміють характер перетворень в залежності від аргументу і числового коефіцієнта. Але перш ніж перейти до роботи з тригонометричними функціями, слід змінити інтервали по осі абсцис (треба, щоб позначки були в радіанах). Для цього вибираємо на панелі інструментів віконечко «Графики», клацаємо лівою кнопкою миші і вибираємо «набор свойств», а потім «тригонометрический набор».

Приклад 6

Побудувати графіки функцій:

 

Y=sin(2x)

 

 

 

 

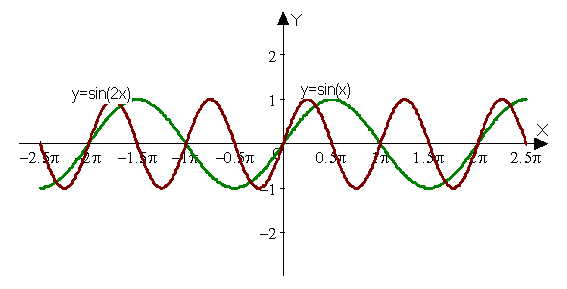
Y=sin(x+pi/3)

 

 

 

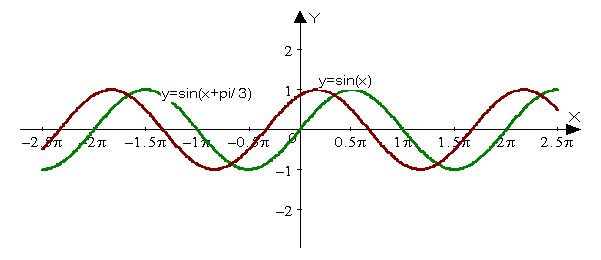
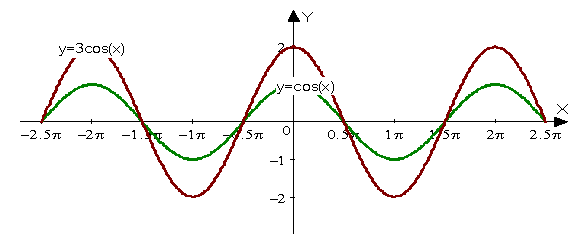
Y=3cos(x)

 

 

 

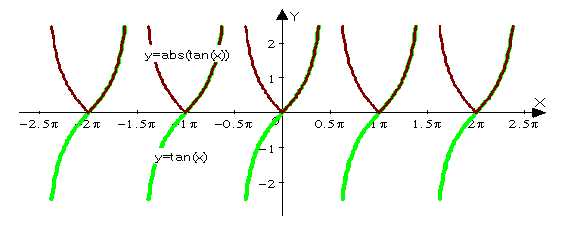
Y=abs(tan(x))

 

 

 

Застосування похідної

  При вивченні теми «Похідна» за допомогою цієї програми можна не тільки будувати графіки функцій, але й досліжувати їх (знаходити екстремуми та нулі функції). Для цього на панелі інструментів вибираємо вікно «исследование функции» і вводимо функцію, яку треба дослідити.

 

Побудова дотичної до графіка фунції

    При вивченні теми «Застосування похідної», учні вчаться знаходити рівняння дотичної до графіка функції в точці за допомогою формули y=f(x₀)+f^/(x₀)(x-x₀). Для наочної інтерпритації цієї теми на уроці закріплення знань доцільно використати цю програму для роботи учнів в парах.

Приклад 7

Записати рівняння дотичної до графіка функції f(x)=x³+2, в точці х₀=1.

Щоб побудувати дотичну і записати її рівняння на комп`ютері 2 учень робить такі дії:

1. Клацає у вікні +F і вводить дану функцію.
2. Клацає у вікні «Касательная или нормаль» і вводить точку дотику і натискає «добавить график».

1 учень виконує вправу в зошиті	2 учень виконує вправу на комп`ютері
у=x3+2 Запишемо рівняння дотичної: y=f(x0)+f/(x0)(x-x0) f(x0)=f(1)=3 f/(x)=3x2 f/(x0)=f/(1)=3 підставимо у рівняння: у=3+3(х-1)=3+3х-3=3х Відповідь: у=3х

 

 

Знаходження площ плоских фігур

Програма дозволяє знаходити площі криволінійних трапецій та фігур, обмежених декількома графіками функцій, за допомогою визначеного інтеграла.

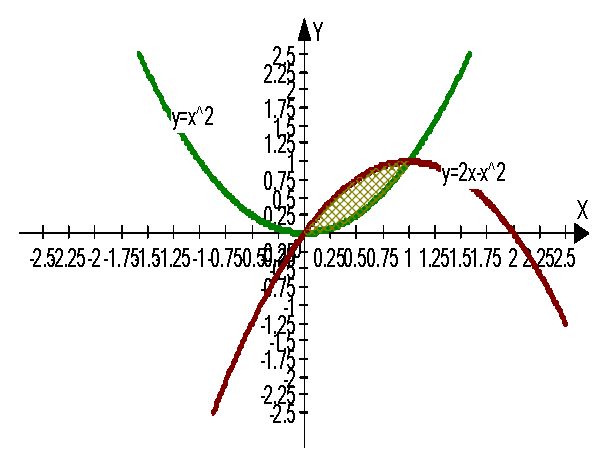
Приклад 8

Знайти площу фігури, обмеженої графіками функцій: Y=x², у=2х-х².

Алгоритм

1 Побудова графіків:

 а) «Графики» - «Добавить график». У вікні «Формула» введіть формулу функції - виберіть товщину лінії - ОК.

 б) Для позначення степеня використовуйте знак ^ (наприклад, х⁴ запишеться х^4)

в). Підписати назву функції: «Правка» - «Добавить метку»

2 Знаходження точок перетину.

 а)«Пересечение». У полі «Формула» введіть формули даних функцій. ОК. З`явиться таблиця з координатами точок перетину, які і будуть межами інтегрування.

3.Обчислення визначеного інтеграла ( знаходження площі).

 а)  «Интегрирование»  вводимо параметри, у верхньому вікні – функцію, що обмежує графік зверху,

у нижньому вікні – функцію, що обмежує графік знизу.

 б) у віконечках «минимум», «максимум» вводимо межі інтегрування. Натискаємо «Считать»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ V.

Використання  презентацій  на уроках математики

    Найдоступнішими і самими поширеними технологіями є застосування табличного процесора MS Excel, програми для створення презентацій Microsoft PowerPoint, пакета динамічної геометрії DG, контрольно-діагностичної системи Test-W. Кожен елемент із зазначеного переліку  програмних засобів є достатньо досконалим у своєму роді. Вважаємо, що використовуючи їх на уроці по черзі або разом, можна значною мірою підвищити ефективність навчально-виховного процесу. Програма для створення презентацій Microsoft PowerPoint є універсальним видом наочності і може бути застосованою у будь-якому класі на уроці будь-якого типу. Та найефективнішим є підготовка та використання презентацій на таких етапах вивчення математики:

• уроки-лекції для пояснення нової теми, де учні не тільки слухають,

   продивляються інформацію на екранах, конспектують, а й відповідають на

    запитання, розв’язують задачі за наведеним зразком;

• для контролю набутих теоретичних знань: на екрані містяться запитання з наступною появою правильної відповіді для самоконтролю;

• для виконання тестових завдань з наступною появою правильної відповіді    після його виконання;

• для проведення усного рахунку;
• інтегровані уроки математики з іншими предметами;
• уроки-подорожі та інше.

 

Прикладом демонстраційного супроводу під час пояснень на уроці  є

презентація теми «Тригонометричні функції».

Пояснення учителя супроводжується інформацією на слайдах, що є не тільки яскравою динамічною ілюстрацією, а й способом фіксації найсуттєвішого у новому матеріалі. Властивості першої тригонометричної функції вчитель пояснює сам, для другої – залучає учнів до пояснень  за готовим малюнком. Для прикладу надані слайди з властивостями двох тригонометричних функцій.

 

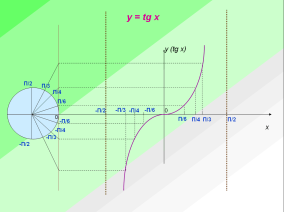
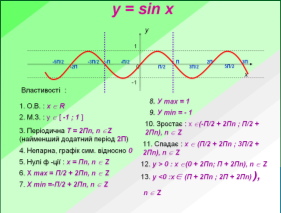
Саме використання мультимедійної дошки дає можливість пропонувати учням неординарні, частково-пошукові завдання на визначення закономірностей, на знаходження  принципу розташування чисел,  математичні кросворди, різноманітну наочність,  супроводжувати звуковими ефектами, економить час на виконання геометричних побудов. А все це надає можливість показати учням математику з найпривабливішого боку, викликати в дитини радість і задоволення від занять розумовою працею, зацікавити предметом.

 

Робота з учнями 5-6 класів має свою специфіку, оскільки поряд з навчальною ігрова діяльність займає в ній важливе місце. Навчальні ігри мають на меті, крім засвоєння навчального матеріалу, вмінь і навичок, ще й надання учневі можливості самовизначення, розвитку творчих здібностей, сприяють емоційному сприймання змісту навчання.

 

Досить ефективно використовувати слайди для проведення тестування з наступною появою правильних варіантів відповідей після їх виконання. На екран проектується тест, після виконання якого учні обмінюються зошитами і здійснюють взаємоперевірку.

Систематичне використання комп’ютерних презентацій на уроках знімає актуальне питання наочності з математики. Більше того, постає інше питання – чи варто витрачати невеликі шкільні ресурси для придбання наочності, зокрема традиційних таблиць, плакатів тощо, якщо можна подати їх у вигляді презентації.

 

За допомогою ПК зручно проводити поточне оцінювання у вигляді тестів. Для цього можна використовувати програму створення тестів TESTW. Вихідний тест може мати  будь-яку  кількість питань (рекомендується від 30 до 50 і більше). З вихідного тесту методом випадкового вибору послідовно виводиться задана  кількість питань (наприклад, 25). Таким чином, кожен учень одержує свій відмінний від сусідів набір питань, що забезпечує індивідуалізацію  і  об'єктивність оцінки. На кожне питання тесту пропонується 5 варіантів відповідей, серед яких від одного до трьох вірних. Учню треба  вказати правильні, на його думку відповіді і перейти до наступного питання.  Час відповіді на тест обмежений. Рекомендується проводити тестування на протязі 10-15 хвилин для кількості питань 20-25.

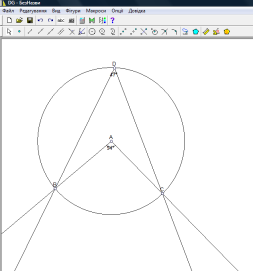
На замовлення Міністерства освіти й науки України було розроблено програмні засоби навчального призначення з різних предметів шкільного курсу, в тому числі з математики. Коли постає питання створення рисунків геометричних фігур, розв’язування задач на побудову, про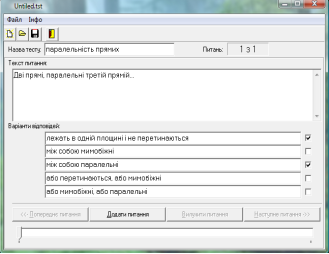ведення досліджень властивостей геометричного місця точок площини, пропонуємо використовувати пакет динамічної геометрії. Наприклад, при вивченні теми «Кути, вписані в коло» в 9класі можна провести урок навчального дослідження, на якому запропонувати різним групам учнів за допомогою програмного середовища дослідити залежність величини вписаного й центрального кутів, якщо вони спираються на спільну дугу ; дослідити величини вписаних кутів, які спираються на одну і ту саму хорду ; перевірити, що кут між хордою АВ і дотичною до кола, що проходить через точку А, дорівнює половині дуги АВ. Після виконання роботи доповідач від кожної групи звітує про її роботу. Перед проведенням такого дослідження учні на уроці інформатики ознайомлюються з роботою  даного програмного середовища.

Вважаємо, що тісна співпраця вчителів математики та інформатики якісно змінює результати учнів з обох дисциплін. Викладання математики при цьому набуває більш динамічної форми, а інформатика стає для учня прикладною.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновок

Робота вчителя – постійний пошук. Сьогодні, в умовах лавини інформації, яка звалюється на кожного учня, від учителя вимагається велика майстерність, щоб підтримати стійкий інтерес своїх вихованців  до навчання.  Завдання вчителя – розвивати розумову активність учня, пропонуючи йому завдання, які відповідають його індивідуальним нахилам, спонукають його до активної співпраці, сприяють формуванню основних груп компетентностей.

 В сучасному світі потреба у комп’ютерних технологіях постійно зростає – вони необхідні і вдома, і на робочому місці. Школа не може собі дозволити залишатися осторонь, тому є потреба і вчителям, і учням добре володіти комп’ютером.  Не секрет, що учні дуже багато часу проводять за комп’ютером, віддаючи його іграм або „мандрівкам” мережею Інтернету. Тому вчителям потрібно спрямувати цей інтерес до комп’ютера в напрямку навчання. Це дасть можливість:

• розширити межі творчої діяльності учнів;
• усвідомити можливість ефективного застосування комп’ютерних технологій у навчанні;
• привчити учнів до самостійної дослідницької діяльності під час розв’язування завдань практичного спрямування;
• розширити можливості навчального процесу, використовуючи комп’ютер для спілкування, проведення досліджень, створення публікацій, презентацій та Web-сайтів, пошуку додаткової інформації тощо.

 Зрозуміло, що кожна технологія і методика мають межі свого застосування, свої переваги та недоліки. Оприлюднення й апробацію інноваційних педагогічних технологій і методик, їх впровадження у процес навчання учнів у школі та надання молодому вчителеві допомоги в цьому мають забезпечити відповідні методичні служби та мережа центрів післядипломної педагогічної освіти.

Отже, використання інформаційно-комунікаційних технологій на навчальних заняттях з математики сприяють активізації навчально-пізнавальної діяльності учнів, швидкому та ефективному засвоєнню ними навчального матеріалу, формуванню ключових компетенцій.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література

1.     Конституція України; 
2.     Закон України «Про освіту»;
3.     Закон України «Про Концепцію Національної програми інформатизації»;
4. Постанова Верховної Ради України від 06.07.2000р. № 1851-III«Про
   затвердження Завдань Національної програми інформатизації на 2000-2002 роки»;
5. Указ Президента України від 31.07.2000 року № 928/2000 «Про заходи щодо розвитку національної складової глобальної інформаційної мережі Інтернет та забезпечення широкого доступу до цієї мережі в Україні»;
6. Наказ Міністерства освіти і науки України « Про проведення експерименту за програмою «Intel ® Навчання для майбутнього», щодо навчання вчителів    використанню    інформаційно-комунікаційних   технологій   у навчально-виховному процесі» від № 749 від 22.09.2004 р.
7. Наказ МОН України № 745 від 21 вересня 2004р. «Про організаційні заходи щодо впровадження зовнішнього оцінювання та моніторингу якості освіти учнів загальноосвітніх навчальних закладів»;

8. «Національна програма виховання дітей та учнівської молоді в Україні( 2004-2013р.р.)»
9.  Закон України « Про Концепцію Державної цільової соціальної програми підвищення якості шкільної природничо-математичної освіти на період до 2015 року»;

10. Архіпова, Т. Л. Вплив нових інформаційних технологій на активізацію навчально-пізнавальної діяльності підлітків / Т.Л. Архіпова. - С .160-167

11.Зайцева, Т. В. Використання комп'ютерних програм на уроках алгебри та початків аналізу / Т.В. Зайцева. - С .101-112

12. Раков С.А., Горох В.П., Осенков К.О., Думчикова О.В., Костіна О.В., Ларін О.Р., Лисиця В.Т., Пікалова В.В. Відкриття геометрії через комп’ютерні експерименти в  пакеті DG. – Харків: ХДПУ, 2002. – 108 с.

13. М.І.Жалдак Комп’ютер на уроках математики. Київ «Техніка»1998

14. WEB-cайти:

http://www.mon.gov.ua/education/average;

http://ostriv.in.ua/index.php?option=com_remository&Itemid=1341&func=fileinfo&parent=folder&filecatid=1 –  програма TEST-W О.Шестопалова;

http://www.mon.gov.ua— офіційний сайтМіністерстваосв1ти та науки України;

http://www.apsu.org.ua— Національна Академія педагогічних наук України;

http://testportal.org.ua/ — Центр тестування при МОЗ України;

http://itc.ua/ko — Компьютерное обозрение ;

http://www.mycomp.com.ua/ — Мой компьютер;

http://itc.ua/dpk — Домашний ПК;

http://www.chip.com.ua — CHIP.