Використання загальних прийомів евристичної діяльності на уроках стереометрії як засіб підвищення рівня навчальних досягнень учнів
Матеріали упорядковані з метою надання допомоги з питань організації рівневого навчання учнів на уроках стереометрії у загальноосвітніх навчальних закладах з використанням евристичних прийомів (тема “Тіла обертання”).
Призначені для використання вчителями математики.
Управління освіти виконавчого комітету
Методичний кабінет
Використання загальних прийомів евристичної діяльності на уроках стереометрії як засіб підвищення рівня навчальних досягнень учнів
Кислюк О.О.
вчитель математики
НВК № 3 м. Шепетівки
2010
Укладач:
О.О. Кислюк, вчитель математики НВК №3 м. Шепетівки
Матеріали упорядковані з метою надання допомоги з питань організації рівневого навчання учнів на уроках стереометрії у загальноосвітніх навчальних закладах з використанням евристичних прийомів (тема “Тіла обертання”).
Призначені для використання вчителями математики.
Зміст
1. Основні вимоги до рівнів навчальних досягнень учня
Перелік використаної літератури
Вступ
У наш час особливо актуальною є об’єктивна потреба в активному розвиткові інтелектуально-творчого потенціалу кожної особи, нації, суспільства в цілому. У реалізації цього завдання провідна роль належить освіті, навчанню. Проте практика свідчить, що процес навчання творчості ще не став нормою в освітніх закладах. Це означає, що людинознавчому аспектові навчання не завжди відводиться належне місце.
Розв’язання зазначеної проблеми потребує пошуку, розробки та впровадження адекватних дидактичних технологій, методів та форм організації навчального процесу, які містять достатній потенціал для створення ситуацій творчого розвитку учнів. Одним із засобів стимулювання творчого саморозвитку учнів сучасна психолого-педагогічна наука визначає евристичне навчання.
Проаналізуємо поняття евристики, евристичного навчання у філософському, психологічному та педагогічному аспектах.
Розглянемо характеристику евристики як спеціальної системи знань.
- Евристики – це прийоми розв’язання певних класів задач, що не піддаються чіткій алгоритмізації.
- Евристики – це прийоми міркувань правдоподібного характеру.
- Евристики – це специфічні розумові прийоми, що складають пошукові стратегії і тактики.
У методичній і психологічній літературі евристичними методами називають будь-які методи, що спрямовані на скорочення перебору розв’язків.
Упровадження методичної системи організації і управління евристичною діяльністю учнів в класах при вивчені стереометрії забезпечує високі результати навчання і створює сприятливі умови для формування прийомів евристичної діяльності школярів.
Для успішного засвоєння учнями стереометрії рекомендується використовувати евристичні прийоми, що покращують рівень навчальних досягнень учнів при розв’язуванні стереометричних задач.
Усі прийоми евристичної діяльності поділяються на загальні і спеціальні. До загальних прийомів евристичної діяльності відносяться:
- Порівняння і аналогія.
- Узагальнення і конкретизація.
- Аналіз і синтез.
Розглянемо зміст загальних прийомів евристичної діяльності та їх операційний склад.
Порівняння і аналогія
Порівняння і аналогія – загальні прийоми евристичної діяльності, що використовуються як в наукових дослідженнях з математики, так і в навчанні математики. За допомогою порівняння виявляються схожість і відмінність стереометричних об’єктів, що порівнюються, тобто наявність у них спільних і відмінних властивостей. Порівняння готує підставу для застосування аналогії, при якій відбувається перенесення інформації про ознаки і відношення з одного стереометричного об’єкта на інший на основі певного зв’язку між ними.
Висновок за аналогією тільки правдоподібний, але не завжди вірний, і тому підлягає ще доведенню. Не варто уникати виникнення хибних висловлень за аналогією. В цьому випадку слід вважати їх гіпотезами. Оскільки найчастіше пошук, дослідження ведуться способом “спроб і помилок”, то помилки, які при цьому допускаються, цілком правомірні. В евристичній діяльності помилки неминучі. Важливо, щоб учні самостійно могли знаходити помилковість “припущень, які виникають у пошуку правильних відповідей”.
Узагальнення і конкретизація
Узагальнення – це мислене виділення, фіксування яких-небудь загальних істотних властивостей, які належать певному класу об’єктів або відношень. Під узагальненням розуміють також перехід від одиничного до загального, від менш загального до більш загального.
Під конкретизацією розуміють зворотний перехід – від більш загального до менш загального, від загального до одиничного.
Навчити учнів узагальнювати задачі можна, якщо вони постійно будуть практикуватися у виконанні завдань на застосування різних прийомів, узагальнених після засвоєння схеми узагальнення. Тому після розв’язання конкретної стереометричної задачі доцільно пропонувати учням завдання на її узагальнення.
Прийом узагальнення через відкидання обмежень широко використовується при вивченні стереометрії, використовуючи аналогію з планіметрією.
Аналіз і синтез
У математиці під аналізом розуміють міркування від невідомого, від того, що треба знайти чи довести, до відомого, до того, що вже знайдено або дано, а під синтезом – міркування від того, що дано, до того, що треба знайти чи довести.
Аналіз є засобом пошуку розв’язання, доведення, хоча сам по собі у більшості випадків не є розв’язанням, доведенням. Синтез дає розв’язання задачі або доведення теореми.
Таким чином, наведена система прийомів евристичної діяльності старшокласників необхідна для успішного вивчення ними шкільного курсу стереометрії.
1. Основні вимоги до рівнів навчальних досягнень учня
Учні повинні вміти:
Початковий рівень:
- Розпізнавати один з кількох запропонованих математичних об’єктів.
- Виконувати одно крокові дії з числами, прочитати і записати даний математичний вираз чи формулу.
- Порівнювати словесно описані математичні об’єкти за їх властивостями.
Середній рівень:
- Зобразити найпростіші геометричні фігури (намалювати ескізи).
- Впізнавати окремі математичні об’єкти і пояснити свій вибір.
- Відтворити означення математичних понять і формулювання тверджень.
- Виконувати за зразком елементарні завдання.
- Відтворювати інформацію, операцію, дію в тому вигляді і в тій послідовності, як вони подавались у процесі навчання, а також в процесі відповіді може допускати окремі видозміни навчальної інформації, наводити власні приклади.
Достатній рівень:
- Застосовувати означення математичних понять та їх властивості до розв’язування завдань у знайомих або змінених ситуаціях.
- Застосовувати залежності між елементами математичних об’єктів.
- Вільно володіти визначеним програмою навчальним матеріалом, самостійно виконувати завдання.
Високий рівень:
- Усвідомлювати нові для нього математичні факти, ідеї, використати набуті знання і вміння в незнайомих для нього ситуаціях.
- Вільно і правильно висловлювати відповідні математичні міркування, переконливо аргументувати їх; самостійно знаходити джерела інформації та працювати з ними.
-
Виявляти варіативність мислення і раціональність у виборі способу розв’язування математичної проблеми у межах вимог навчальної програми; розв’язувати нестандартні задачі у межах вимог навчальної програми.
2. Використання загальних прийомів евристичної діяльності на уроках стереометрії як засіб підвищення навчальних досягнень учнів
Середній рівень навчальних досягнень
Порівняння і аналогія
Пригадавши з учнями операційний склад прийому порівняння, організовуємо роботу для його формування. Потім вони складають під керівництвом вчителя орієнтовну основу діяльності (ООД). Рекомендується використати перший тип ООД:
- Встановити мету порівняння: чи завжди переріз кулі площиною є кругом?
- Перевірити, чи знають учні означення кулі, перерізу кулі, круга.
- Скласти план порівняння: сформулювати означення кулі і круга, засвоїти основні знання, що використовуються.
4. Знайти схожі властивості, для цього порівняти означення цих понять, використовуючи прийом порівняння.
Розв’язуючи задачу “Радіус циліндра 2 м, висота 3 м. Знайти діагональ осьового перерізу”, учні виділяють операційний склад прийому:
- Виконати малюнок, повторити означення циліндра, осьового перерізу циліндра, його радіуса, висоти.
- Скласти план діяльності: порівняти означення циліндра, прямого циліндра з умовою задачі.
- Сформулювати висновок: “Не так важливо, який циліндр розглядати, оскільки всі дані для обчислення діагоналі відомі в умові задачі”.
Тут треба наголосити, що дана стереометрична задача зводиться до розв’язання планіметричної задачі: “Знайдіть діагональ прямокутника, якщо його сторони дорівнюють 4 м і 3 м відповідно”. Також необхідно наголосити, що тут використовується прийом аналогії, тобто ми використовуємо цей прийом, коли, аналізуючи стереометричну задачу, говоримо, що дану задачу ми можемо звести до планіметричної, не порушивши умови.
Далі учні переходять до відпрацювання операцій:
-
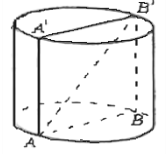
Виконаємо малюнок і пригадаємо потрібні нам означення. - Осьовий переріз АА'В'В – прямокутник, основа якого дорівнює діаметру основи циліндра, тобто 4 м, а висота – 3 м.
- Із прямокутного трикутника ∆АВ'В за теоремою Піфагора одержимо:
![]() (см).
(см).
Прямокутний трикутник ∆АВ'В є, як відомо з 7 класу, єгипетським трикутником. А тому можна було одразу зробити висновок, що діагональ осьового перерізу циліндра дорівнює 5 см.
Отже, діагональ осьового перерізу циліндра дорівнює 5 см.
Як бачимо, в даній задачі ми використали прийом порівняння, коли порівнювали циліндр з прямим циліндром, і використали прийом аналогії, коли звели розв’язання стереометричної задачі до розв’язання планіметричної задачі, яку учні вже вміють без труднощів розв’язувати.
Розв’язуючи задачу “Радіус основи конуса дорівнює 3 м, твірна – 5 м. Знайти площу осьового перерізу”, учні виділяють операційний склад прийому:
- Виконати малюнок, повторити означення конуса, осьового перерізу конуса, його радіуса, твірної.
- Скласти план діяльності: порівняти означення конуса, прямого конуса з умовою задачі та зробити висновок, що використовуючи прийом порівняння та аналогії між властивостями конуса та прямого конуса, не так важливо, який конус розглядати, оскільки всі дані для обчислення осьового перерізу конуса відомі в умові задачі (використовуємо прийом порівняння).
Далі учні переходять до відпрацювання операцій:
-
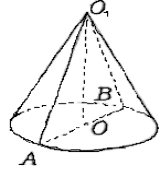
Виконаємо малюнок і пригадаємо потрібні нам означення.
Використовуючи аналогію з планіметрією можемо сказати, що нам потрібно розв’язати планіметричну задачу про трикутник в якій потрібно відшукати його площу за заданими двома сторонами.
- З прямокутного трикутника ∆АОО1 за теоремою Піфагора:
![]() (см).
(см).
![]() (см2).
(см2).
Отже, площа осьового перерізу конуса дорівнює 12 см2.
Розв’язуючи задачу “Радіус основи зрізаного конуса дорівнює 3 м і 6м, а висота 4 м. Знайдіть твірну зрізаного конуса”, учні виділяють операційний склад прийому:
- Виконати малюнок, повторити означення конуса, зрізаного конуса, його радіуса, твірної.
- Скласти план діяльності: розглянути осьовий переріз конуса і дослідити всі дані, які нам дано в задачі. Зробити висновок про те, що дано і що треба знайти.
- Сформулювати висновок: “Оскільки осьовим перерізом зрізаного конуса є рівнобічна трапеція і її основи дорівнюють відповідно двом радіусам основ зрізаного конуса, то достатньо, використовуючи аналогію, розв’язати таку планіметричну задачу: “У рівнобічної трапеції основи відповідно дорівнюють 6 м і 12 м, а висота – 4 м. Знайдіть бічну сторону””. Тут потрібно наголосити, що ми для проведених міркувань використали прийом порівняння та аналогії. А саме, наголосили, що дану стереометричну задачу можна порівняти, використовуючи прийом аналогії, з планіметричною задачею, що дасть нам потрібний результат. Прийом порівняння ми використовували, коли розглядали осьовий переріз зрізаного конуса, де говорилося про те, що він є рівнобічною трапецію, і подальше розв’язання даної задачі зводиться до відшукання її бічної сторони.
Далі учні переходять до відпрацювання операцій:
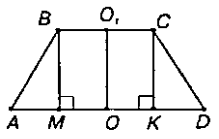
Виконаємо малюнок і пригадаємо потрібні нам означення.
Оскільки ВСКМ – прямокутник, бо ВМ і СК – висоти трапеції, то ВМ=СК і ∆АВМ=∆DСК. Тому КD=АМ=0,5(АD-ВС)=3 (м).
В прямокутному ∆АВМ за теоремою Піфагора:
![]() (м).
(м).
Отже, бічна сторона рівнобічної трапеції дорівнює 5 м. Ми розв’язали планіметричну задачу, а отже і стереометричну. Звідси робимо висновок, що твірна зрізаного конуса дорівнює 5 м.
Розглянемо задачу “У циліндрі паралельно його осі проведено площину, що перетинає основу по хорді. Діагональ утвореного перерізу дорівнює d і утворює з площиною основи кут β. Знайдіть площу перерізу циліндра”.
Після того, як учні пригадали суть прийому аналогії, вчитель з учнями переходить до аналізу задачі:
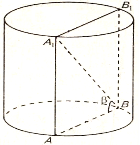
Нехай дано циліндр, у якого паралельно його осі ОО1 проведено переріз АВВ1А1, який є прямокутником. За умовою <АВА1=β, А1В=d.
Проаналізувавши дану задачу, учні бачать, використовуючи прийом порівняння, що перерізом циліндра є прямокутник і для розв’язання даної задачі, використовуючи прийом аналогії, досить розв’язати таку планіметричну задачу: “У прямокутнику діагональ дорівнює d і утворює з меншою стороною кут β. Знайти площу прямокутника”.
Вчитель: Що необхідно для розв’язання цієї планіметричної задачі?
Учні: Знайти сторони прямокутника.
Вчитель: Що ще потрібно зробити?
Учні: Ми маємо усі дані для обчислення площі цього прямокутника, отже, обчислюємо її.
Вчитель: Чому дорівнює площа прямокутника?
Учні: ![]()
Далі під керівництвом вчителя учні переходять до роздільного відпрацювання операцій:
- Будуємо зображення циліндра і його перерізу.
- Формулюємо, використовуючи прийом аналогії, планіметричну задачу.
- Розв’язуємо сформульовану планіметричну задачу:
AA1=A1B*sin β=d sin β,
AB=A1B*cos β=d cos β.
Отже,
![]() .
.
Таким чином, площа шуканого перерізу циліндра дорівнює ![]() .
.
Отже, ми розв’язали планіметричну задачу. Відповідно робимо висновок, що знайдена відповідь є розв’язком і стереометричної задачі.
Як бачимо, розв’язуючи кожну стереометричну задачу, ми використовували прийом порівняння, коли розглядали перерізи геометричних тіл, і використовували прийом аналогії, коли формулювали планіметричну задачу. Учні помічають, що кожна задача такого типу розв’язується, формулюючи відповідну планіметричну задачу, використовуючи прийоми порівняння та аналогії. Така побудова розв’язання задач значно полегшує розв’язання цих задач і підвищу не тільки рівень знань учнів, але й рівень зацікавленості математикою.
Узагальнення та конкретизація
Формування прийомів узагальнення і конкретизації корисно здійснювати під час розв’язування такої задачі: “Через вершину конуса проведено площину під кутом 450 до основи. Площина перетинає основу по хорді, що дорівнює радіусу основи конуса. Знайти об’єм конуса, якщо відстань від його вершини до хорди дорівнює 6 см”.
Пригадавши означення конуса та його властивості, суть прийому узагальнення та формулу для обчислення об’єму конуса учитель наголошує, що розміри конуса можуть бути різними. Тому відстань від вершини конуса до хорди можна позначити в загальному випадку через а см, а кут позначити через α. Після запитання вчителя: “Чи можна сформулювати узагальнену задачу?” старшокласники формулюють узагальнену задачу: “Через вершину конуса проведено площину під кутом α до основи. Площина перетинає основу по хорді, що дорівнює радіусу основи конуса. Знайти об’єм конуса, якщо відстань від його вершини до хорди дорівнює а”. Тут потрібно наголосити, що ми використали прийом узагальнення, коли сформулювали узагальнену задачу до даної.
Роздільне відпрацювання операцій в даній задачі таке:
- Пригадати означення конуса та формулу для обчислення його об’єму.
Об’єм конуса ![]() .
.
- Сформулювати узагальнену задачу, розв’язати її.
Задача: “Через вершину конуса проведено площину під кутом α до основи. Площина перетинає основу по хорді, що дорівнює радіусу основи конуса. Знайти об’єм конуса, якщо відстань від його вершини до хорди дорівнює а”.
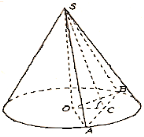
Розв’яжемо дану задачу:
∆АОВ рівносторонній (за умовою), ∆АSВ рівнобедрений (АS=SВ).
SО=SC sin α=a sin α, OC=SC cos α=a cos α.
З ∆АОС (<О=300, <А=600, <С=900):
![]() .
.
![]() .
.
- Зробити висновок: отже, для того, щоб розв’язати задачу, можна спочатку розв’язати її в загальному вигляді, а потім підставити числові значення в отриманий результат, одержимо розв’язок початкової задачі.
- Отже, підставимо в отриманий результат початкові дані. Отримаємо:
![]() (см3).
(см3).
Тут потрібно наголосити, що в пункті 3-4 ми використали прийом конкретизації, тобто у виведену нами формулу підставили конкретні дані з умови задачі і отримали розв’язок початкової задачі.
Формування даних прийомів корисно здійснювати і під час розв’язування такої задачі: “В рівносторонньому конусі (осьовий переріз – правильний трикутник) радіус основи 4 см. Знайдіть площу перерізу, проведеного через дві твірні, кут між якими дорівнює 450”.
Аналогічно, пригадавши означення конуса та його властивості, суть прийому узагальнення та формулу для обчислення площі перерізу конуса, учитель наголошує, що розміри конуса можуть бути різними. Тому природньо їх позначити в загальному випадку через R см радіус основи конуса і кут між твірними через α. Після запитання вчителя: “Чи можна сформулювати узагальнену задачу?”, старшокласники формулюють узагальнену задачу: “В рівносторонньому конусі (осьовий переріз – правильний трикутник) радіус основи дорівнює R см. Знайдіть площу перерізу, проведеного через дві твірні, кут між якими дорівнює α”. Тут потрібно наголосити, що в цьому випадку ми використовуємо прийом узагальнення.
Роздільне відпрацювання операцій в даній задачі таке:
- Згадати означення конуса та формулу для обчислення його осьового перерізу.
Означення: Конусом називається тіло, яке складається з круга – основи конуса, точки, яка не лежить у площині цього круга – вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи.
Площа осьового перерізу конуса, тобто площа трикутника дорівнює
![]() .
.
- Сформулювати узагальнену задачу, розв’язати її.
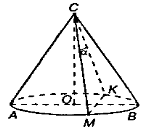
Виконаємо малюнок:
Оскільки в осьовому перерізі конуса правильний трикутник, то АС=АВ=2R. Площу ∆МСК знайдемо за формулою:
![]() .
.
Підставимо числові значення в знайдену формулу, використовуючи прийом конкретизації, і отримаємо відповідь до задачі:
![]() (см2).
(см2).
Розглянемо задачу: “Куля, радіус якої R, перетнуто площиною на відстані с від центра. Знайдіть площу перерізу”.
Спочатку учні пригадують, що називається кулею, її радіусом, що є її перерізом і чому він дорівнює.
Означення: Кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань радіусом кулі.
Теорема: Переріз кулі площиною є круг.
Оскільки перерізом кулі є круг, то ми можемо конкретизувати нашу задачу, тобто ми можемо розглянути конкретну задачу з планіметрії до якої зведемо нашу стереометричну задачу. Отже, нам потрібно знайти площу розглядуваного круга. Для цього спочатку знайдемо його радіус.
Звернемо увагу на те, що нам в задачі задано не числові величини сторін цього трикутника. Ми можемо розглянути спочатку дану задачу, а потім у відповідь підставити будь-які конкретні значення для обчислення конкретного значення, якщо це потрібно.
Перейдемо до відпрацювання операцій:
-
Виконуємо малюнок і пригадуємо потрібні для розв’язання задачі означення. - Виділяємо, що дано і що потрібно знайти.
- Розв’язуємо задачу:
В прямокутному трикутнику ∆АОВ за теоремою Піфагора:
![]() .
.
Тоді площа перерізу дорівнює ![]() .
.
Отже, ми отримали потрібний нам результат. А тепер підставимо деякі конкретні значення для перевірки правильності формули, наприклад, нехай R=41 см, а с=9 см. Одержимо,
![]() .
.
Отже, як бачимо, оскільки ми отримали деяке конкретне додатне число, то дану формулу ми знайшли правильно.
Розглянемо задачу: “Дах башти має форму конуса. Висота даху 2 м, діаметр башти 6 м. Знайдіть поверхню даху”.
Пригадавши означення конуса та його властивості, суть прийому узагальнення та формулу для обчислення поверхні конуса, учитель наголошує, що розміри конуса можуть бути різними. Тому природньо їх позначити в загальному випадку через h висоту конуса і діаметр основи через d. Після запитання вчителя: “Чи можна сформулювати узагальнену задачу?”, старшокласники формулюють узагальнену задачу: “Дах башти має форму конуса. Висота даху h, діаметр башти d. Знайдіть поверхню даху”.
Тут потрібно наголосити, що в цьому випадку ми використовуємо прийом узагальнення.
Роздільне відпрацювання операцій в даній задачі таке:
- Згадати означення конуса та формулу для обчислення його поверхні.
Площа поверхні конуса дорівнює
![]()
- Сформулювати узагальнену задачу, розв’язати її.
Виконаємо малюнок:
Розглянемо трикутник АСВ: ![]() .
.
В прямокутному трикутнику СВО за теоремою Піфагора
![]() .
.
Отже, ![]() .
.
- Використовуючи прийом конкретизації, підставимо числові дані з задачі в отриманий результат, одержимо:
![]() .
.
Як бачимо, у розглянутих задачах ми застосовували прийом узагальнення, коли узагальнювали дану задачу за допомогою буквених величин, і використовували прийом конкретизації, коли підставляли числові дані в одержаний результат.
Аналіз і синтез
Формування даних прийомів корисно здійснювати під час розв’язування такої задачі: “На поверхні кулі дано три точки. Прямолінійні відстані між ними 6 см, 8 см, 10 см. Радіус кулі 13 см. Знайти відстань від центра до площини, яка проходить через ці точки”.
Пригадавши суть прийомів аналізу і синтезу, ми ставимо питання учням відповідно до операційного складу прийомів (проводимо аналіз).
Вчитель: Сформулюйте мету нашого дослідження.
Учні: Знайти відстань від центра до площини, яка проходить через ці точки.
Вчитель: Який перший крок дослідження?
Учні: Потрібно пригадати означення кулі, її радіуса.
Вчитель: Що необхідно для розв’язання задачі?
Учні: (Використовується прийом аналізу) Проведемо ОО1 перпендикулярно площині ∆АВС. Тоді прямокутні трикутники АО1О, ВО1О, СО1О рівні за катетом і гіпотенузою (оскільки АО=ВО=СО – радіус кулі і ОО1 – спільний катет). Отже, О1 – центр кола, описаного навколо трикутника АВС. Зауважимо, що 62+82=102. Тому трикутник АВС прямокутний. Через це О1 – середина АС. Отже, АО1=5 см.
Вчитель: Що залишилося ще зробити?
Учні: Знайти шукану відстань з прямокутного трикутника АОО1.
Після цього учні під керівництвом вчителя переходять до роздільного відпрацювання операцій (синтезу):
-
Будуємо зображення кулі. - Позначаємо на ній дані точки і проводимо її радіус.
- В прямокутному трикутнику АОО1 за теоремою Піфагора:
![]() (см).
(см).
- Отже, шукана відстань дорівнює 12 см.
Формування прийомів аналізу і синтезу доцільно проводити також за допомогою такої задачі: “Рівностороній трикутник обертається навколо своєї сторони а. Знайдіть об’єм отриманого тіла обертання”.
Виконаємо малюнок і перейдемо до проведення аналізу задачі
Аналіз: Як ми знаємо, в результаті обертання трикутника навколо своєї сторони ми отримаємо два конуси. Отже, для відшукання об’єму утвореного тіла обертання, необхідно знайти об’єм конуса і помножити його на два.
З рівностороннього трикутнику АВС знайдемо висоту конуса і радіус основи:
![]() .
.
Тоді об’єм отриманого тіла обертання дорівнює сумі об’єму двох однакових конусів з радіусом ВО і висотою АО=ОС (використовуємо прийом синтезу).
Тобто ![]() .
.
Формування прийомів аналізу і синтезу доцільно проводити також за допомогою такої задачі: “Повна поверхня рівностороннього конуса рівновелика поверхні кулі, яка побудована на його висоті як на діаметрі. Доведіть це”.
Виконаємо малюнок та провівши потрібні міркування, використовуючи прийом аналізу, доведемо, що повна поверхня рівностороннього конуса рівновелика поверхні кулі, побудованій на його висоті як на діаметрі.
Проведемо аналіз задачі, використовуючи прийом аналізу.
Оскільки трикутник АВС рівносторонній, то ![]() .
.
Тоді бічна поверхня дорівнює ![]() .
.
А повна поверхня буде дорівнювати:
![]() .
.
Повна поверхня рівностороннього конуса позначимо через S0 і вона дорівнює ![]() .
.
Далі розглянемо осьовий переріз. Тоді в рівносторонньому трикутнику АВС висота ![]() .
.
Тоді ![]() і площа поверхні кулі дорівнює
і площа поверхні кулі дорівнює
![]() .
.
Отже, дійсно повна поверхня рівностороннього конуса рівновелика поверхні кулі, побудованій на його висоті як на діаметрі. При цьому слід наголосити, що ми використовували прийом синтезу, як прийом міркування від того, що дано, до того, що треба знайти чи довести.
Як показує практика, розв’язання задач, використовуючи прийоми аналізу та синтезу, сприяють кращій активності учнів на уроках. Адже, учні самі, проводячи потрібні міркування, поступово приходять до розв’язання даної задачі. При цьому вони спочатку використовують аналіз, тобто аналізують дану задачу, а потім, використовуючи прийом синтезу та проведені міркування, розв’язують без труднощів поставлену перед ними задачу.
Отже, використання аналізу та синтезу на уроках при розв’язуванні задач, стимулює в учнів бажання до пошуку розв’язків та інтерес до відкриття нових знань.
Достатній рівень навчальних досягнень
Порівняння і аналогія
Використовуючи задачу “Радіуси основ зрізаного конуса 3 дм і 7 дм, твірна 5 дм. Знайдіть площу осьового перерізу”, в учнів можна формувати прийоми порівняння і аналогії на достатньому рівні наступним чином.
Пригадавши суть прийому аналогії, у відповідності з його операційним складом проводимо аналіз задачі.
Для аналізу задачі використаємо малюнок:
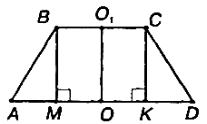
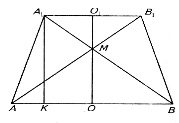
Пригадавши означення конуса, зрізаного конуса, старшокласники роблять висновок, що осьовим перерізом зрізаного конуса є рівнобічна трапеція, (використовують прийом порівняння). Провівши аналіз умови задачі і врахувавши останній висновок, учні під керівництвом вчителя, використовуючи аналогію, формулюють аналогічну планіметричну задачу: “В рівнобічній трапеції бічна сторона дорівнює 5 см, а основи 6 см і 14 см відповідно. Знайдіть площу цієї трапеції”.
Тепер переходимо до розподільного відпрацювання операцій:
-
Для знаходження площі трапеції нам потрібно мати її висоту і основи. Проведемо висоти ВМ
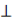 АD і СК
АD і СК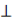 АD. Основи ми маємо за умовою задачі, а висоту знайдемо з прямокутного трикутника ∆АВМ.
АD. Основи ми маємо за умовою задачі, а висоту знайдемо з прямокутного трикутника ∆АВМ.
Отже, ВС=МК і ВМ=СК. Тоді ВСКМ – прямокутник. ∆АВМ=∆СКD, так що KD=АМ=(АD-ВС)*0,5=4 (см).
У прямокутному ∆АВМ за теоремою Піфагора отримаємо:
![]() (дм).
(дм).
Тоді ![]() (дм2).
(дм2).
Отже, ми знайшли площу осьового перерізу зрізаного конуса.
До наведеної задачі ми можемо навести і задачу обернену до даної, яка теж формує прийоми порівняння і аналогії, а саме: “Радіуси основ зрізаного конуса R і r, а твірна нахилена до основи під кутом 450. Знайдіть висоту”.
Пригадавши суть прийому аналогії, у відповідності з його операційним складом проводимо аналіз задачі.
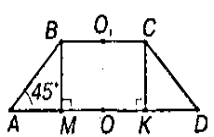
Для аналізу задачі використаємо малюнок:
Пригадавши означення конуса, зрізаного конуса, старшокласники роблять висновок (використовуючи прийом порівняння), що осьовим перерізом зрізаного конуса є рівнобічна трапеція. Провівши аналіз умови задачі і врахувавши останній висновок, учні під керівництвом вчителя (використовуючи прийом аналогії) формулюють планіметричну задачу: “В рівнобічній трапеції основи дорівнюють 2r і 2R відповідно. Кут при основі дорівнює 450. Знайдіть висоту трапеції”.
Тепер переходимо до розподільного відпрацювання операцій.
Проведемо висоти ВМ![]() АD і СК
АD і СК![]() АD. Основи ми маємо за умовою задачі, а висоту знайдемо з прямокутного трикутника ∆АВМ.
АD. Основи ми маємо за умовою задачі, а висоту знайдемо з прямокутного трикутника ∆АВМ.
Отже, ВС=МК і ВМ=СК. Тоді ВСКМ – прямокутник. ∆АВМ=∆СКD, так що KD=АМ=0,5(АD-ВС)=R-r.
У рівнобедреному ∆АМВ<А=<АВМ=450.
Тоді Н=ВМ=АМ=R-r.
Отже, розв’язавши планіметричну задачу, ми одержали розв’язок і стереометричної задачу. Тобто, висота зрізаного конуса дорівнює висоті рівнобічної трапеції і дорівнює R-r.
Формування прийому порівняння на достатньому рівні ми пропонуємо учням за допомогою розв’язання такої задачі: “Діаметр кулі 25 см. На її поверхні дано точка А і круг, всі точки якого віддалені (по прямій) від А на 15см. Знайдіть радіус цього круга”.
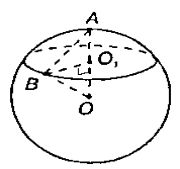
Пригадавши суть прийому порівняння та його операційний склад, проводимо аналіз задачі.
Виконаємо малюнок:
Пригадавши означення кулі та її властивості, учні приходять до висновку, що для розв’язання даної задачі необхідно розв’язати аналогічну планіметричну задачу, використовуючи прийом аналогії: “Дано рівнобедрений трикутник АОВ, у якого дві сторони по 12,5 см, а третя – 15 см. Знайдіть висоту ВО проведену з вершини В на сторону ОА”. Тут потрібно наголосити, що для формулювання допоміжної задачі ми використали аналогію цієї задачі з планіметричною задачею. Але це ми могли зробити після того, як провели порівняння двох геометричних фігур: кулі та круга.
Після цього переходимо до відпрацювання операцій:
∆АОВ рівнобедрений (оскільки ОВ=ОА) і АВ=15 см.
Знайдемо площу цього трикутника за формулою Герона:
![]() (см).
(см).
Але ![]() , тоді
, тоді
![]() (см).
(см).
Отже, розв’язавши дану планіметричну задачу, ми одержали розв’язок і стереометричної задачі.
Формування прийому порівняння можна розглядати і на такій задачі: “Твірна конуса нахилена до площини основи під кутом β. Знайдіть об’єм конуса, якщо радіус описаної навколо нього кулі дорівнює R”.

Пригадавши суть прийому порівняння та його операційний склад, проводимо аналіз задачі.
Виконаємо малюнок:
Пригадавши означення конуса, кулі та їх властивості, учні приходять до висновку, що для розв’язання даної задачі необхідно розв’язати таку планіметричну задачу: “У рівнобедреному трикутнику кут при основі дорівнює β. Навколо трикутника описано коло, радіус якого дорівнює R. Знайти висоту даного трикутника”. Розв’язавши дану планіметричну задачу, ми отримаємо усі потрібні величини для обчислення об’єму конуса, вписаного в кулю стереометричної задачі.
Розв’яжемо планіметричну задачу:
Розглянемо осьовий переріз конуса і кулі. SO – висота трикутника ∆SАВ, SА=SВ. <SВА=β. О1 – центр описаного навколо трикутника кола, О1S=О1В=R. В ∆АSВ центр О1 описаного кола лежить на прямій, що містить висоту SО. З ∆АВS за наслідком з теореми синусів:
![]() , AB=2R*sin (1800-2β)=2R*sin 2β.
, AB=2R*sin (1800-2β)=2R*sin 2β.
OB=0,5*AB=R*sin 2β;
З ∆SOB (<O=900):
![]() .
.
Ми одержали усі необхідні для розв’язання стереометричної задачі дані, розв’язавши планіметричну задачу. Підставимо отримані дані у формулу для обчислення об’єму конуса. Отримаємо:
![]() .
.
Таким чином, розв’язавши спочатку планіметричну задачу, ми отримали необхідні дані для розв’язання стереометричної задачі.
Як бачимо, використання прийомів порівняння і аналогії значно полегшує розв’язання задач. Особливо помітно це при розв’язанні задач достатнього рівня, де для розв’язання задачі потрібно використовувати не тільки знання означень, теорем чи формул, а й проводити деякі міркування.
Узагальнення та конкретизація
Розглянемо задачу: “Через вершину конуса проведено площину, яка перетинає основу по хорді, яку видно з центра основи під кутом 600, а з вершини під кутом 900. Знайти площу перерізу, якщо бічна поверхня конуса дорівнює 10 см”.
Пригадавши суть даних прийомів, учням ставляться питання відповідно до їх операційного складу.
Вчитель: Встановіть мету дослідження.
Учні: Знайти площу перерізу.
Вчитель: Яка наступна дія нашого дослідження?
Учні: Виконати малюнок, пригадати означення конуса та його властивості.
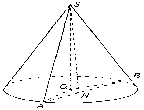
Отже, виконаємо малюнок:
Вчитель: Чи можна, проаналізувавши властивості конуса, сформулювати задачу, для якої дана задача є узагальненою чи конкретизованою? Який з загальних прийомів евристичної діяльності ми використаємо при цьому?
Учні: Можемо сформулювати задачу, що є узагальненою по відношенню до даної задачі: “Через вершину конуса проведено площину, яка перетинає основу по хорді, яку видно з центра основи під кутом β, а з вершини під кутом α. Знайти площу перерізу, якщо бічна поверхня конуса дорівнює Р”. При формулюванні даної задачі ми використали прийом узагальнення.
Вчитель: Що необхідно зробити для розв’язання задачі?
Учні: Проведемо ![]() . Тоді
. Тоді ![]()
![]() .
.
Вчитель: Чи можемо ми розв’язати цю задачу зразу, чи потрібні ще якісь дані?
Учні: Введемо допоміжну зміну, тобто нехай ![]()
Вчитель: Давайте розв’яжемо цю задачу спочатку в загальному вигляді, а потім підставимо конкретні числові значення.
Учні: З ![]()
З 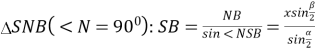 .
.
Тоді 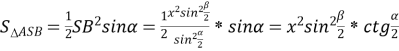 .
.
Оскільки 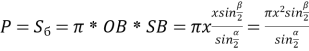 , то
, то 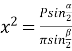 .
. 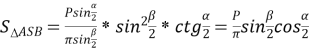 .
.
Тепер підставимо числові значення, при цьому використаємо прийом конкретизації. Будемо мати:
![]()
Отже, ![]() (см).
(см).
Розглянемо задачу: “У конус вписано правильну чотирикутну піраміду. Висота і радіус конуса відповідно дорівнюють h і r см. Знайдіть бічне ребро, основу і апофему піраміди”.
Пригадавши суть даних прийомів, учням ставляться питання відповідно до їх операційного складу.
Вчитель: Яка мета нашого дослідження?
Учні: Знайти бічне ребро, основу і апофему піраміди.
Вчитель: Яка наступна дія нашого дослідження?
Учні: Виконати малюнок, пригадати означення конуса, його висоти, радіуса, означення піраміди, її бічного ребра, сторони основи і апофеми, а також формулу для відшукання площі її основи.
Вчитель: Чи можна, проаналізувавши умову задачі, сформувати задачу, для якої дана задача є узагальненою чи конкретизованою?
Учні: Можемо сформулювати задачу, яка є конкретизованою по відношенню до даної задачі: “У конус вписано правильну чотирикутну піраміду. Висота і радіус конуса відповідно дорівнюють 1 і ![]() см. Знайдіть бічне ребро, основу і апофему піраміди”.
см. Знайдіть бічне ребро, основу і апофему піраміди”.
Вчитель: Що необхідно зробити для розв’язання цієї допоміжної задачі?
Учні: Розглянути прямокутний трикутник ∆SOA і визначити з нього бічне ребро піраміди. Провести ще один радіус ОВ і з рівнобедреного трикутника ∆АОВ знайти сторону основи піраміди. Розглянемо прямокутний трикутник ∆SМD і визначимо апофему піраміди, пам’ятаючи, що апофема – це висота бічної грані піраміди.
Далі учні під керівництвом вчителя переходять до роздільного відпрацювання операцій:
-
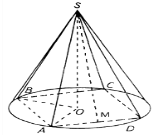
Будуємо зображення вписаної в конус правильної чотирикутної піраміди. -
Формулюємо конкретизовану задачу “У конус вписано правильну чотирикутну піраміду. Висота і радіус конуса відповідно дорівнюють 1 см і
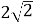 см. Знайдіть бічне ребро, основу і апофему піраміди”.
см. Знайдіть бічне ребро, основу і апофему піраміди”.
- Розв’язуємо поставлену задачу:
З ∆ SOA за теоремою Піфагора
![]() (см).
(см).
З ∆ АОВ АО=ОВ за теоремою Піфагора
![]() (см).
(см).
З ∆ SМD за теоремою Піфагора
![]() (см).
(см).
У попередніх задачах ми розв’язували спочатку узагальнену задачу, а потім конкретизовану. А в даній задачі, як бачимо, навпаки.
Дані прийоми можна формулювати і на такій задачі: “В основі прямої призми лежить прямокутній трикутник з гіпотенузою 4 см і гострим кутом 450. Діагональ грані, що містить протилежний до даного кута катет, нахилена до площини основи під кутом 300. Знайти бічну поверхню циліндра, вписаного в дану призму”.
Пригадавши суть даних прийомів, учням ставляться питання відповідно до їх операційного складу.
Вчитель: Встановіть мету дослідження.
Учні: Знайти бічну поверхню циліндра, вписаного в призму.
Вчитель: Яка наступна дія нашого дослідження?
Учні: Виконати малюнок, пригадати означення призми, циліндра, призми, описаної навколо циліндра та їх властивості.
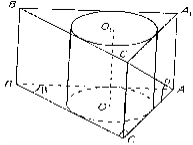
Отже, виконаємо малюнок:
Вчитель: Чи можна, проаналізувавши умову задачі, сформулювати задачу, для якої дана задача є узагальненою чи конкретизованою?
Учні: Можемо сформулювати задачу, яка є узагальненою по відношенню до даної задачі, використовуючи прийом узагальнення: “В основі прямої призми лежить прямокутній трикутник з гіпотенузою с і гострим кутом β. Діагональ грані, що містить протилежний до даного кута катет, нахилена до площини основи під кутом α. Знайти бічну поверхню циліндра, вписаного в дану призму”.
Вчитель: Що необхідно зробити для розв’язання цієї задачі?
Учні: Нехай АВСА1В1С1 – дана призма, основою якої є ∆АВС, в якому <С=900, <В=β, АВ=с. Проекцією діагоналі АС1 на площину основи є відрізок АС. Тому за умовою <С1АС=α. Висота Н=ОО1 циліндра, вписаного в дану призму, дорівнює висоті призми, а радіус основи r – радіус кола, вписаного в ∆АВС. Sб=2πrН.
Вчитель: Ми провели усі необхідні міркування, що будемо робити дальше?
Учні: З ∆АВС (<С=900): AC=c*sin β; BC=c*cos β. Тоді
![]() .
.
З іншого боку ![]() , де р – півпериметр ∆АВС.
, де р – півпериметр ∆АВС.
Оскільки ![]() , то
, то
![]() .
.
З ∆АСС1 (<С=900): H=CC1=AC*tg α=c*sin β*tg α.
Отже, ![]() .
.
Таким чином, ми розв’язали поставлену перед нами узагальнену задачу. Для розв’язання початкової задачі необхідно, використовуючи прийом конкретизації, в одержаний результат підставити числові значення величин. Тоді будемо мати:
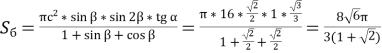 (см).
(см).
Отже, ми отримали потрібний результат. Як бачимо, розв’язання спочатку узагальненої задачі дає можливість підставити в одержаний результат будь-які конкретні значення. У даному конкретному випадку, було б не досить зручно користуватися отриманими величинами, які є ірраціональними числами, з самого початку задачі. Тобто інколи краще спочатку розв’язати узагальнену задачу, а потім підставити в результат конкретні значення.
Розглянемо задачу: “В основі піраміди лежить прямокутник, площа якого дорівнює S і кут між діагоналями дорівнює α. Всі бічні ребра піраміди нахилені до площини основи під кутом β. Знайти об’єм конуса, описаного навколо цієї піраміди”.
На розв’язанні цієї задачі розглянемо прийоми формування конкретизації та узагальнення. Як бачимо, дана задача є узагальненням деякої задачі, в якій задано було б числові значення кутів та площі. Розв’яжемо її:
-
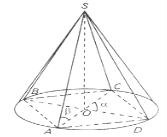
Виконаємо малюнок і проаналізуємо умову задачі:
Нехай SАВСD – дана піраміда, основою якої є прямокутник АВСD, SАВСD=S. О – точка перетину діагоналей АС і ВD, <СОD=α. Оскільки бічні ребра піраміди утворюють з площиною основи один і той же кут, то вершина S проектується в центр кола, описаного навколо прямокутника, тобто в точку О. Отже, SО![]() (АВС) і за умовою <SАО=β.
(АВС) і за умовою <SАО=β.
- Розглянемо прямокутник АВСD. З нього знайдемо діагональ АС. Як було встановлено раніше, R=АО=0,5АС. Потім з прямокутного трикутника ∆SОА знайдемо одну з його сторін, яка є висотою конуса. Оскільки усі необхідні елементи у нас будуть, то ми можемо знайти об’єм конуса, описаного навколо піраміди.
![]() .
.
Звідси ![]() .
. ![]()
З ∆SОА (<О=900): ![]() .
.
Тоді ![]() .
.
Можна розглянути таку конкретизовану задачу, використовуючи при цьому прийом конкретизації: “В основі піраміди лежить прямокутник, площа якого дорівнює 4 см і кут між діагоналями дорівнює 300. Всі бічні ребра піраміди нахилені до площини основи під кутом 450. Знайти об’єм конуса, описаного навколо цієї піраміди”.
Отже, при розв’язанні даної задачі ми отримали відповідь, тобто формулу, яка задає об’єм конуса в даному випадку. Підставимо деякі конкретні значення і одержимо значення об’єму. Будемо мати:
![]() (см3).
(см3).
Розглянемо формування цих прийомів на такій задачі: “Діагоналі ромба 15 см і 20 см. Кульова поверхня дотикається до його сторін. Радіус кулі 10 см. Знайдіть відстань від центра кулі до площини ромба”.
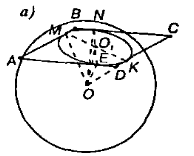
Виконаємо малюнок (малюнок а) і проаналізуємо задачу:
Проведемо перпендикуляр ОО1 до площини ромба. Відрізки OM=ON=OK=OE=10 см і перпендикулярні відповідним сторонам ромба. Тоді за теоремою про три перпендикуляри О1М, O1N, О1К і О1Е перпендикулярні відповідним сторонам ромба. Дальше, ΔΟΟ1Μ=ΔΟO1N=ΔОО1К=ΔOO1E (за гіпотенузою і катетом). Отже, O1M=O1N=O1K=O1E і це означає, що О1 – центр вписаного в ромб кола (малюнок б).
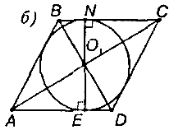
Дана задача, використовуючи прийом аналогії, зводиться до розв’язання планіметричної задачі: “Діагоналі ромба 15 см і 20 см. У нього вписано коло. Знайдіть О1Е”. Після розв’язання цієї планіметричної задачі ми, маючи усі необхідні величини, повернемося до розв’язання стереометричної задачі.
В прямокутному ΔAΟ1D (АС![]() BD):
BD):
![]() (см).
(см).
Тоді ![]() .
.
З іншої сторони ![]() .
.
Тоді ![]() .
.
![]()
З прямокутного трикутника ∆ОО1Е:
![]() .
.
Отже, відстань від центра кулі до площини ромба дорівнює 8 см.
Розв’язуючи дані задачі, ми використовували прийоми узагальнення і конкретизації. Як бачимо, дані прийоми допомагають учням розв’язувати задачі, затрачаючи на це менше часу. А також при їх розв’язанні учні проявляють свої здібності та творчість, при цьому проявляються їхні знання евристичних методів.
Аналіз і синтез
Задача “Довести, що якщо в осьовий переріз зрізаного конуса можна вписати коло, то його висота є середня пропорційна між діаметрами основ”.
Після того, як учні пригадають суть названих евристичних прийомів, їм ставляться питання відповідно до операційного складу цих прийомів (проводиться аналіз).
Вчитель: Що необхідно для розв’язання задачі?
Учні:
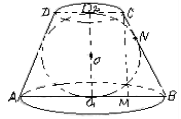
Проводимо аналіз задачі. Нехай в осьовий пeрeріз ABCD зрізаного конуса вписано коло з центром О.
Позначимо AO1=R, DО2=r, О2О1=Н, AD=L. Треба довести, що ![]() .
.
Осьовим перерізом є рівнобічна трапеція ABCD. З точки С на АВ опустимо перпендикуляр CM![]() AB; тоді
AB; тоді
![]() .
.
За властивістю дотичних проведених з однієї і тієї ж самої точки до кола, ![]() .
.
Звідси, ![]() .
.
(Синтез) З прямокутного трикутника ∆ СМВ (<М=900) знаходимо
![]() , що й треба було довести.
, що й треба було довести.
Розв’язуючи задачу “Бічне ребро правильної трикутної піраміди дорівнює 5 см, сторона основи – 6 см. У дану піраміду вписано конус. Знайти твірну, радіус і висоту конуса, а також площу осьового перерізу конуса”, учні під керівництвом вчителя спочатку пригадують операційний склад прийомів аналізу і синтезу, потім виконують роздільне відпрацювання операцій та складання ООД під керівництвом вчителя:
- Аналіз (проводимо аналіз задачі, використовуючи прийом аналізу). Встановити мету: Обчислити твірну, радіус і висоту конуса, а також обчислити площу осьового перерізу конуса.
- Пригадати означення конуса, його твірної, радіуса і висоти, а також що є осьовим перерізом конуса.
-
Скласти план. Учні ставлять перед собою питання: “Як обчислити радіус вписаного в рівносторонній трикутник кола?”. Відповідають, що радіус вписаного в правильний трикутник кола дорівнює
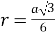 . “Що є осьовим перерізом конуса?” Відповідають, що осьовим перерізом конуса є рівнобедрений трикутник.
. “Що є осьовим перерізом конуса?” Відповідають, що осьовим перерізом конуса є рівнобедрений трикутник.
-
Проведемо деякі міркування: Оскільки твірну конуса ми можемо знайти з прямокутного трикутника ∆AKS, для радіуса основи конуса ми знаємо формулу, а висоту ми знайдемо з прямокутного трикутника ∆SOK. Площу осьового перерізу конуса, тобто площу рівнобедреного трикутника ми можемо знайти за формулою:
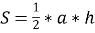 .
.
-
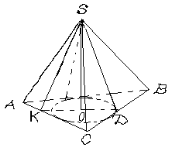
Сформулювати висновок: “Оскільки ми маємо усі дані для обчислення того, що вимагається в задачі, то можемо безпосередньо підставити дані з умови в отримані формули”.
Переходимо до роздільного відпрацювання операцій (синтез), при цьому використовуємо прийом синтезу:
- З прямокутного трикутника ∆ AKS за теоремою Піфагора
![]() (см).
(см).
-
А
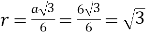 (см).
(см).
- З прямокутного трикутника ∆ SOK за теоремою Піфагора:
![]() (см).
(см).
-
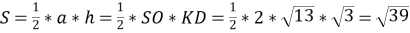 (см).
(см).
Під час розв’язування даних задач учнями використовується другий тип ООД, оскільки учням даються всі вказівки, як правильно виконувати дії чи завдання. При кожному повторенні дії пункти евристичної схеми, що складені нами, виступають для учнів опорними точками, необхідною умовою правильного виконання дії.
Розв’язуючи задачу “Переріз кулі площиною, що знаходиться на відстані 12 см від її центра, має площу 25π см2. Знайти площу поверхні кулі”, учні під керівництвом вчителя спочатку пригадують операційний склад прийомів аналізу і синтезу, потім виконують роздільне відпрацювання операцій та складання ООД під керівництвом вчителя (проводять аналіз задачі, використовуючи прийом аналізу):
- Встановити мету дослідження: знайти площу поверхні кулі.
- Пригадати означення кулі, її властивості.
- Скласти план: виконуємо малюнок, пригадуємо потрібні нам означення, аналізуємо дані задачі, робимо висновок про те, що нам дано в задачі і що потрібно знайти, розв’язуємо задачу.
Аналіз: Нехай (О, ОА) – дана куля.
![]()
![]() Учні ставлять перед собою питання “Що таке куля?” і відповідають, що кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань радіусом кулі. Далі їх цікавить таке питання: “Що утвориться при перерізі кулі площиною?” Відповідають, що якщо відстань від центра О кулі до площини α менша її радіуса, то площина перетинає поверхню кулі по колу з центром О1. Наступне питання в учнів таке: “Чому дорівнює площа перерізу і як визначити радіус кулі?”. Старшокласники відповідають: оскільки ОО1=12см, О1А=r, де А – довільна точка одержаного кола і площа перерізу дорівнює 25πсм2, то πr2=25π, звідки r=5 см.
Учні ставлять перед собою питання “Що таке куля?” і відповідають, що кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань радіусом кулі. Далі їх цікавить таке питання: “Що утвориться при перерізі кулі площиною?” Відповідають, що якщо відстань від центра О кулі до площини α менша її радіуса, то площина перетинає поверхню кулі по колу з центром О1. Наступне питання в учнів таке: “Чому дорівнює площа перерізу і як визначити радіус кулі?”. Старшокласники відповідають: оскільки ОО1=12см, О1А=r, де А – довільна точка одержаного кола і площа перерізу дорівнює 25πсм2, то πr2=25π, звідки r=5 см.
Синтез: (після проведених міркувань розв’язуємо дану задачу, використовуючи прийом синтезу). З означення перпендикулярності прямої і площини маємо, що ОО1![]() О1А.
О1А.
Тому з ∆ОО1А: ![]() .
. ![]() .
.
У процесі розв’язування даних задач учням не даються вказівки, як виконувати дії, їм пропонується лише зразок дії і називається її результат. Вони самі шукають правильний спосіб розв’язування методом спроб та помилок і в результаті цієї діяльності вчаться виконувати дану дію правильно. Однак, міцна навичка в учнів не створюється, вони не можуть перенести дану дію на нові знання.
Формувати прийоми аналізу та синтезу можна і на такій задачі: “Знайти об’єм меншого кульового сектора кулі, якщо радіус кола його основи дорівнює 60 см, а радіус кулі – 75 см”.
Далі учні під керівництвом вчителя спочатку пригадують операційний склад прийомів аналізу і синтезу, потім виконують роздільне відпрацювання операцій та складання ООД під керівництвом вчителя (аналіз):
- Встановити мету дослідження: знайти об’єм меншого кульового сектора кулі.
- Пригадати означення кулі, її властивості.
- Скласти план: виконуємо малюнок, пригадуємо потрібні нам означення, аналізуємо дані задачі, робимо висновок про те, що нам дано в задачі і що потрібно знайти, розв’язуємо задачу.
Аналіз: (проводимо аналіз задачі, використовуючи прийом аналізу). Розглянемо осьовий переріз АОВDА даного кульового сектора. ![]() , де R – радіус кулі, а Н – висота відповідного сегмента. Знайдемо Н.
, де R – радіус кулі, а Н – висота відповідного сегмента. Знайдемо Н.
Синтез: (після проведення аналізу, розв’язуємо дану задачу, використовуючи при цьому прийом синтезу). Проведемо ОD![]() АВ. Тоді О1А – радіус кола основи сектора. За умовою О1А=60 см і R=ОА=75 см. З ∆ОАО1 (<О1=900):
АВ. Тоді О1А – радіус кола основи сектора. За умовою О1А=60 см і R=ОА=75 см. З ∆ОАО1 (<О1=900):
![]() (см).
(см).
Н=ОD-ОО1=R-ОО1=75-45=30 (см).
![]() (см3).
(см3).
Отже, об’єм меншого кульового сектора кулі дорівнює 112500π (см3).
Розглянемо задачу: “У нижній основі циліндра проведено хорду, яку видно з її центра під кутом β. Відрізок, що сполучає центр верхньої основи з серединою цієї хорди, нахилений до площини основи під кутом α. Знайдіть бічну поверхню циліндра, якщо відстань від центра нижньої основи до цього відрізка дорівнює d”.
Пригадавши суть прийомів аналізу і синтезу, ми ставимо питання учням відповідно до операційного складу прийомів (проводимо аналіз задачі, використовуючи прийом аналізу).
Вчитель: Сформулюйте мету нашого дослідження.
Учні: Знайти бічну поверхню циліндра.
Вчитель: Який перший крок дослідження?
Учні: Потрібно пригадати означення циліндра та його властивості.
Вчитель: Що необхідно для розв’язання задачі?
Учні: Проведемо аналіз: Нехай дано циліндр з віссю ОО1, АВ – хорда нижньої основи, <АОВ=β, АМ=МВ. Проекція відрізка О1М на площину основи є відрізок ОМ. Тому за умовою <О1МО=α. З точки О проведемо ON![]() O1M. За умовою ОN=d.
O1M. За умовою ОN=d.
Площа бічної поверхні циліндра дорівнює Sб=2πRH.
Після цього учні під керівництвом вчителя переходять до роздільного відпрацювання операцій (використовуємо прийом синтезу):
- Будуємо зображення циліндра:
- Розглянемо відповідні трикутники з малюнка і знайдемо необхідні нам елементи для відшукання бічної поверхні циліндра.
З ∆ОNМ (<N=900): ![]() .
.
З ∆O1OM (<O=900): ![]() .
.
Оскільки ОА=ОВ, то в ∆АОВ медіана ОМ є одночасно висотою і бісектрисою. Тому <ОМА=900, <АОМ=β/2.
З ∆ АОМ (<М=900): ![]() .
.
Тоді ![]() .
.
Формування аналізу і синтезу можна розглядати і на такій задачі: “Через вершину конуса проведено площину під кутом α до площини основи. Ця площина перетинає основу по хорді, яку видно з центра основи конуса під кутом β. Знайти об’єм конуса, якщо відстань від центра основи до перерізу дорівнює d”.
Пригадавши суть прийомів аналізу і синтезу, ми ставимо питання учням відповідно до операційного складу прийомів (проводимо аналіз задачі).
Вчитель: Сформулюйте мету нашого дослідження.
Учні: Знайти об’єм конуса.
Вчитель: Який перший крок дослідження?
Учні: Потрібно пригадати означення конуса, формулу для обчислення об’єму конуса.
Вчитель: Що необхідно для розв’язання задачі?
Учні: Проведемо аналіз даної задачі, використовуючи прийом аналізу: Нехай трикутник ∆АSВ – його переріз. Проведемо SМ![]() АВ. Тоді ОМ
АВ. Тоді ОМ![]() АВ за теоремою про три перпендикуляри і за умовою <SМО=α. З точки О проведемо ОN
АВ за теоремою про три перпендикуляри і за умовою <SМО=α. З точки О проведемо ОN![]() АSВ, ОN=d.
АSВ, ОN=d.
Вчитель: Що залишилося ще зробити?
Учні: Знайти висоту і радіус конуса з ∆SОМ і ∆ОМА.
Після цього учні під керівництвом вчителя переходять до роздільного відпрацювання операцій (проводять синтезу, використовуючи прийом синтезу):
-
Будуємо зображення конуса і наносимо на нього усі потрібні нам для розв’язання позначення. -
З ∆ SОМ (<О=900):
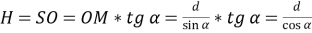 .
.
-
З ∆ OMA (<M=900):
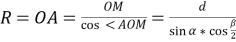 .
.
-
Тоді
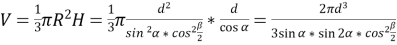 .
.
Під час розв’язування даних задач учнями використовується другий тип ООД, оскільки учням даються всі вказівки, як правильно виконувати дії чи завдання. При кожному повторенні дії пункти евристичної схеми, що складені нами, виступають для учнів опорними точками, необхідною умовою правильного виконання дії.
Формування даних прийомів можна розглянути і на такій задачі: “Паралельно осі циліндра проведено площину, яка відтинає від кола основи дугу β. Відрізок, який сполучає центр основи циліндра з точкою кола іншої основи, дорівнює а і утворює з площиною основи кут α. Знайти площу перерізу”.
Пригадавши суть прийомів аналізу і синтезу, ми ставимо питання учням відповідно до операційного складу прийомів (проводимо аналіз).
Вчитель: Яка мета нашого дослідження?
Учні: Знайти площу перерізу.
Вчитель: Який перший крок дослідження?
Учні: Потрібно пригадати означення циліндра, формулу для обчислення його перерізу.
Вчитель: Що необхідно для розв’язання задачі?
Учні: Проведемо аналіз задачі, використовуючи прийом аналізу: Нехай дано циліндр. Площина, паралельна його осі ОО1, перетинає його по прямокутнику АВВ1А1. S=АВ*ВВ1.
Після цього учні під керівництвом вчителя переходять до роздільного відпрацювання операцій (синтезу), при цьому використовуємо загальний прийом евристичної діяльності – синтез:
-
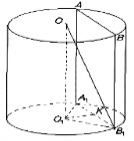
Будуємо зображення циліндра і наносимо на нього усі потрібні нам для розв’язання позначення. - З ∆ОВ1О1 (<О1=900): ОО1=ОВ1*sin α=a*sin α. OO1=BB1=H, O1B1=R,
-
Проведемо О1К
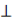 А1В1. Тоді А1К=КВ1.
А1В1. Тоді А1К=КВ1.
-
З ∆О1КВ1 (<К=900):
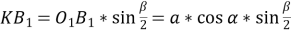 ,
,
![]() .
.
![]() .
.
Таким чином, на розв’язанні даних задач ми розглянули формування прийомів аналізу і синтезу.
Розглянемо застосування даного прийому на достатньому рівні при розв’язуванні такої, наприклад, задачі: “Твірна зрізаного конуса нахилена до площини основи під кутом α. Радіуси основ R і r (r<R). Знайти площу бічної поверхні зрізаного конуса”.
Розв’яжемо цю задачу:
Учитель: Спочатку виконаємо малюнок.
Далі перейдемо до аналізу даної задачі, використовуючи прийом аналізу:
Дано зрізаний конус, круг (О;ОА) i круг (О1;О1В) – основи, ОА=R, О1В=r, α – кут нахилу АВ до площини основи. Знайти S6.
![]() , де r і R – радіуси основи, l – твірна.
, де r і R – радіуси основи, l – твірна.
Учитель: Отже, ми чітко виділили, що дано в задачі і що треба знайти. Як будемо міркувати далі?
Учні: ОА i O1B – прямі перетину паралельних площин основ зрізаного конуса площиною АВО1О, то за властивістю паралельних площин OA||O1B. Отже, за означенням АВО1О – трапеція з основами ОA i О1В. Оскільки ОО1 – висота зрізаного конуса ОО1||(круг (О;ОА)), то О1О||ОА.
Проведемо ВН||ОО1. Тоді ВН||ОА. Отже, за означенням OO1ВH – паралелограм з прямим кутом ВНО, то ОО1ВН – прямокутник. Тоді О1В=ОН=r і тоді АН=ОА-ОН=R-r.
ВН – перпендикуляр, проведений з точки В до площини нижньої основи зрізаного конуса, ВА – похила, то АН – її проекція. Тоді за означенням кута між прямою і площиною <OAB – кут нахилу АВ до площини основи. За умовою <OAB=α.
Учитель: Що ж випливає з даних міркувань?
Учні: (Використовуючи прийом синтезу) З ∆АВН: <АНВ=900, <НАВ=α, АН=R-r.
![]() ,
,
тобто ![]() .
.
Отже, ![]() .
.
Як показує практика, застосування аналізу і синтезу для розв’язування задач сприяє кращому засвоєнню вивченого матеріалу. Крім того вміння застосовувати згадані евристичні прийоми сприяє вмінню учнів розв’язувати складні задач. Адже, саме головне при розв’язуванні задач – це вміння аналізувати дану задачу, а також вміти синтезувати одержані дані.
Отже, ми розглянули як можна використовувати загальні прийоми евристичної діяльності на конкретних задачах достатнього рівня. Розв’язання цих задач вже говорить про достатній рівень засвоєння учнями прийомів порівняння і аналогії, узагальнення і конкретизації, аналізу та синтезу.
Високий рівень навчальних досягнень
Порівняння і аналогія
Прийоми порівняння і аналогії на цьому рівні доцільно формувати на такій задачі: “У зрізаному конусі діагоналі осьового перерізу взаємно перпендикулярні, а твірна l утворює з площиною більшої основи кут α. Знайти площу осьового перерізу зрізаного конуса” [95].
Після того, як учні пригадали суть прийому аналогії, вчитель ставить їм питання відповідно до операційного складу прийому.
Нехай АА1В1В – осьовий переріз даного зрізаного конуса, АВ1![]()
![]()
![]() А1В, а кут при основі – α. Знайти площу трапеції”.
А1В, а кут при основі – α. Знайти площу трапеції”.
Вчитель: Що необхідно для розв’язання цієї планіметричної задачі?
Учні: Провести А1К![]()
Вчитель: Що ще потрібно зробити?
Учні: Ми маємо усі дані для обчислення площі трапеції, отже, обчислюємо її.
Вчитель: Чому дорівнює площа трапеції?
Учні: ![]() .
.
Далі під керівництвом вчителя учні переходять до роздільного відпрацювання операцій:
- Будуємо зображення трапеції.
- Формулюємо аналогічну планіметричну задачу (використовуємо прийом аналогії).
- Розв’язуємо дану задачу:
З прямокутного трикутника А1КА знаходимо А1К.
А1К=АА1*sin α=l*sin α.
∆A1MB1 – рівнобедрений, бо ∆A1O1M=∆B1O1M за катетами, а <A1MB1=900, тому <MA1B1=<MB1A1=450, аналогічно <MAB=<MBA=450.
Отже, <A1АB1=α-450.
З ∆АА1М (<М=900): АМ=АА1*cos (α-450)=l* cos (α-450).
A1М=АА1*sin(α-450)=l*sin(α-450).
З ∆АОМ (<О=900):
![]() .
.
![]() .
.
З ∆А1О1М:
![]() .
.
![]() .
.
![]() .
.
Отже, площа перерізу зрізаного конуса дорівнює
![]() .
.
Як бачимо, розв’язуючи планіметричну задачу, ми одержали розв’язок стереометричної задачі.
Прийоми порівняння і аналогії на цьому рівні доцільно формувати також на такій задачі: “Куля радіуса R вписана в зрізаний конус. Кут нахилу твірної до площини нижньої основи конуса дорівнює α. Знайдіть радіуси основ і твірну l конуса”.
Використовуючи прийом порівняння, проводимо аналіз задачі: Розглянувши осьовий переріз зрізаного конуса, учні бачать, що ним є рівнобічна трапеція і формулюють відповідну планіметричну задачу, використовуючи аналогію: “У рівнобічній трапеції кут при основі дорівнює α. В неї вписано коло, радіус якого – R. Знайти сторони основи і бічну сторону трапеції”.
Вчитель: Що необхідно для розв’язання цієї планіметричної задачі?
Учні: Провести ВМ![]()
В ∆АВМ: ![]() .
.
Вчитель: Як будемо міркувати дальше?
Учні: Центр вписаної в трапеції кола лежить на перетині бісектрис, отже, АО і ВО – бісектриси, тобто <ВАО=α/2, <АВО=0,5<АВС=900-α/2.
Вчитель: Що це означає?
Учні: Це означає, що трикутник ∆АВО прямокутний.
Далі під керівництвом вчителя учні переходять до роздільного відпрацювання операцій:
-
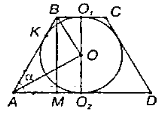
Будуємо зображення перерізу зрізаного конуса, тобто рівнобічну трапецію. - Формулюємо аналогічну планіметричну задачу: “У рівнобічній трапеції кут при основі дорівнює α. В неї вписано коло, радіус якого – R. Знайти сторони основи і бічну сторону трапеції”.
- Розв’язуємо дану планіметричну задачу:
В ∆АВМ: ![]() .
.
З ∆АВО: 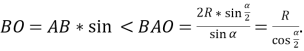
З прямокутного трикутника ∆ ВОО1:
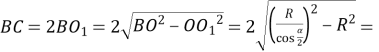
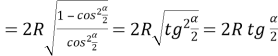 .
.
Оскільки ВК=ВО1 і АО2=АК, то
![]()
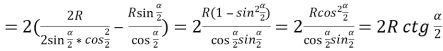 .
.
- Ми розв’язали планіметричну задачу і одержали значення бічної сторони та значення основ трапеції. Це значення відповідає значенню твірної зрізаного конуса. А от значення радіусів основ зрізаного конуса дорівнюють половині знайдених значень основ трапеції. Тому знайдемо радіуси основ зрізаного конуса, поділивши знайдені значення основ рівнобічної трапеції на два. Одержимо:
![]() і
і ![]() , а твірна
, а твірна ![]() .
.
Таким чином, ми розв’язали і стереометричну задачу.
Отже, ми розв’язали задачу, спочатку розв’язавши її першу частину за допомогою розв’язання планіметричної задачі, а потім, одержавши потрібні нам величини, розв’язали стереометричну задачу при цьому використовували необхідні нам прийоми порівняння і узагальнення.
Таким чином, ми спочатку, використовуючи прийом порівняння, проводимо аналіз даної задачі, а потім, використовуючи аналогію з планіметрією, формулюємо планіметричну задачу, розв’язавши яку ми отримуємо розв’язок і стереометричної задачі.
Узагальнення і конкретизація
Формування прийомів узагальнення і конкретизації пропонуємо учням за допомогою такої задачі: “В кулю вписано правильну чотирикутну піраміду, сторона основи якої дорівнює 4 см. Знайти площу поверхні кулі, якщо бічне ребро піраміди нахилене до площини основи під кутом 300”.
Пригадавши суть цих прийомів, відповідно до їх операційного складу проводимо аналіз умови задачі.
Нехай SABCD – дана піраміда, основа ABCD – квадрат, АВ=4 см, <SАС=<SСА=300.
Пригадавши означення правильної чотирикутної піраміди, вписаної в кулю, учні пропонують узагальнити дану задачу, тобто розв’язати її в загальному вигляді, використовуючи при цьому прийом узагальнення, а в одержаний результат підставити числові значення, використовуючи прийом конкретизації. Отже, отримаємо задачу: “В кулю вписано правильну чотирикутну піраміду, сторона основи якої дорівнює а см. Знайти площу поверхні кулі, якщо бічне ребро піраміди нахилене до площини основи під кутом α”.
Розв’яжемо узагальнену задачу:
Точка О – центр вписаної кулі, О належить висоті піраміди SМ. АS=СS, ![]() , <АSМ=900-α.
, <АSМ=900-α.
З ∆АSМ (<М=900): ![]() .
.
З ∆АSО (АО=SО як радіуси):
<АОS=1800-<АSО-<SАО=1800-2<АSО=1800-<АSС.
Але <АSС=<SАО=1800-2α. Отже, <АОS=2α. Тоді <АОS=<SАО=900-α.
За теоремою синусів:
![]() , тобто
, тобто ![]() .
.
Звідки ![]() .
.
Але ОS – радіус сфери, тому
![]() .
.
Отже, ми розв’язали узагальнену задачу. Тому можна розв’язати і початкову задачі, підставивши початкові дані з задачі в отриманий результат (використовуємо прийом конкретизації).
![]() .
.
Формування прийомів узагальнення і конкретизації можна розглянути на такій задачі: “В основі піраміди лежить рівнобедрений трикутник, площа якого 36 см2 і кут при основі 600. Всі бічні грані піраміди нахилені до площини основи під кутом 300. Знайти бічну поверхню конуса, вписаного в дану піраміду”.
Пригадавши означення піраміди, конуса, піраміди, описаної навколо конуса, їх властивості та провівши аналіз умови задачі, учні помічають, що вона є конкретизованою по відношенню до такої задачі: “В основі піраміди лежить рівнобедрений трикутник, площа якого Р і кут при основі β. Всі бічні грані піраміди нахилені до площини основи під кутом α. Знайти бічну поверхню конуса, вписаного в дану піраміду”. Тут потрібно наголосити, що ми використовуємо такий евристичний прийом, як конкретизація.
Провівши аналіз задачі, учні розв’язують узагальнену задачу, а потім в результат підставляють значення даної задачі, тобто розв’язують конкретизовану задачу.
Нехай SАВС – дана піраміда, основою якої є ∆АВС, АВ=ВС, <ВАС=β, S∆АВС=Р.
Нехай SО – висота піраміди. Проведемо SК![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , то
, то ![]() .
.
У ∆АВС ВМ – медіана, висота і бісектриса. З ∆АВМ (<М=900):
![]() .
.
З ∆АОМ (<О=900): ![]() .
.
З ∆ОМS (<О=900): ![]() .
.
Тоді ![]() .
.
Отже, ми розв’язали узагальнену задачу. Тепер підставимо числові значення в одержаний результат, одержимо:
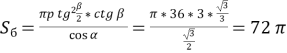 (см2).
(см2).
Як бачимо, для розв’язання задач високого рівня спочатку зручніше розв’язувати узагальнену задачу, а потім в одержаний результат підставляти конкретні числові значення. Це значно спрощує задачу і полегшує її розв’язання.
Формування прийомів узагальнення і конкретизації можна розглянути і на такій задачі: “В основі піраміди лежить трикутник з кутами 300 і 600 і площею 25 см2. Всі бічні ребра піраміди утворюють з її висотою кут 450. Знайти площу поверхні сфери, описаної навколо піраміди”.
Пригадавши означення піраміди; сфери; сфери, описаної навколо піраміди; їх властивості та провівши аналіз умови задачі, учні помічають, що вона є конкретизованою по відношенню до такої задачі: “В основі піраміди лежить трикутник з кутами α і β і площею S. Всі бічні ребра піраміди утворюють з її висотою кут φ. Знайти площу поверхні сфери, описаної навколо піраміди”.
Провівши аналіз задачі, учні розв’язують узагальнену задачу, а потім в результат підставляють значення даної задачі.
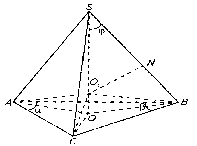
Виконаємо малюнок:
Нехай SАВС – дана піраміда, основа якої є ∆АВС, <ВАС=α, <АВС=β, S∆АВС=S. SО – висота піраміди. За умовою АSО=ВSО=СSО=φ. Нехай О1 – центр сфери, описаної навколо піраміди.
Sсф=4πR2, де R=О1S – її радіус. Позначимо R=х.
З точки О1 проведемо О1N![]()
З ∆ SОВ: ОВ=SВ sin φ=2x cos φ*sin φ=x sin 2φ.
З ∆АВС за наслідком з теореми синусів:
![]() ,
,
AC=2x sin 2φ*sin β, BC=2x sin 2φ*sin α.
Тоді
![]()
![]()
![]()
Звідси ![]() .
.
Отже, ![]() .
.
Підставимо в знайдений результат числові значення кутів і площі, отримаємо:
![]() (см2).
(см2).
Тут потрібно наголосити, ми розв’язували узагальнену задачу, а потім уже конкретизовану. Тому, що на практиці при розв’язувані задач високого рівня простіше розв’язати узагальнену задачу, а потім в отриманий результат підставити конкретні значення.
Розглянемо таку задачу: “У циліндр вписано пряму призму, основою якої є рівнобічна трапеція з гострим кутом 600. Діагональ трапеції є бісектрисою гострого кута. Діагональ бічної грані, що містить бічну сторону трапеції дорівнює 4 см і утворює з площиною основи кут 450. Знайдіть об’єм циліндра”.
Пригадавши означення циліндра, прямої призми, циліндра, описаного навколо призми, їх властивості та провівши аналіз умови задачі, учні помічають, що вона є конкретизованою по відношенню до такої задачі: “У циліндр вписано пряму призму, основою якої є рівнобічна трапеція з гострим кутом α. Діагональ трапеції є бісектрисою гострого кута. Діагональ бічної грані, що містить бічну сторону трапеції дорівнює l і утворює з площиною основи кут γ. Знайдіть об’єм циліндра”.
Учитель: (Провівши аналіз задачі, учні розв’язують узагальнену задачу, а потім в результат підставляють значення даної задачі).
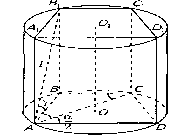
Виконаємо малюнок:
Учитель: З чого розпочнемо розв’язувати задачу?
Учні: Проведемо її аналіз, використовуючи прийом порівняння: нехай АВСDА1В1С1D1 – дана призма, вписана в циліндр, основою якої є трапеція АВСD, АD||ВС, АВ=СD, <ВАD=α, <ВАС=<САD. Оскільки АD||ВС, то <DСА=<ВСА як внутрішні різносторонні кути при паралельних прямих АD і ВС та січній АС. Отже, АВ=ВС. АВ є проекцією діагоналі В1А на площину основи. Тому за умовою В1А=l і <В1АВ=γ.
Учитель: Що далі?
Учні: З ∆АВ1В (<В=900): AB=BC=D1F cosγ=l cos. H=DD1=l sin γ.
V=πR2H, де H=ОО1=DD1, R – радіус кола, описаного навколо трапеції ABCD.
Учитель: Що з цього випливає?
Учні: Цей радіус є радіусом кола, описаного навколо трикутника ∆АВС. За наслідком з теореми синусів маємо:
![]() .
.
![]() .
.
Учитель: Що будемо робити далі?
Учні: Перейдемо від узагальнення даної задачі до її конкретизації, тобто підставимо числові значення в знайдену формулу, одержимо:
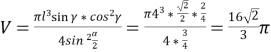 (см2).
(см2).
Практика свідчить, що розв’язання учнями задач з використанням прийомів узагальнення та конкретизації, значно підвищує їх рівень сформованості та стимулює математичну творчість. Адже, учні постійно творчо працюють над даними задачі, роблять висновки, формулюють узагальнені чи конкретизовані задачі. Часте використовування на практиці згаданих прийомів евристичної діяльності розвиває їхні знання і вміння застосовувати ці прийоми при розв’язуванні задач.
Аналіз і синтез
Аналіз є основою досить загального підходу до розв’язування задач, відомого під назвою зведення задачі до сукупності підзадач.
Ідея такого підходу полягає саме у властивому для аналізу “міркуванні у зворотному напрямі” від задачі, яку треба розв’язати, до підзадач, потім від цих підзадач до ще простіших підзадач і т.д., поки вихідна (первинна) задача не буде зведена до набору елементарних задач.
Розглянемо формування аналізу та синтезу на прикладі такої задачі: “Через дві твірні конуса, які утворюють між собою кут α, проведено площину, що перетинає основу по хорді, яку видно з центра основи під кутом β. Знайти бічну поверхню конуса, якщо відстань від центра основи до середини твірної дорівнює d”.
Учитель: Виконаємо малюнок і проведемо аналіз задачі:
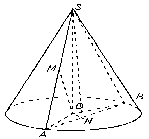
Нехай дано конус з висотою SО, SА, SВ – його твірні, <АSВ=α, <АОВ=β, SМ=МА, ОМ=d. S=πRl, де R=ОА – радіус основи, l=SА – довжина твірної.
Учитель: Як будемо міркувати далі?
Учні: З ∆SОА: ОМ=1/2*SА, тому точка О є центром описаного кола. SА=2ОМ=2d. З точки S проведемо SN![]()
![]()
Тут учням потрібно наголосити, що ми при аналізі задачі використовуємо такий загальний прийом евристичної діяльності, як аналіз.
Учитель: Провівши аналіз задачі, що будемо робити далі?
Учні: (проводимо синтез) З ∆SNА: ![]() .
.
З ∆ONA: 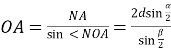 .
.
Учитель: Отже, маючи усі необхідні дані, ми можемо знайти площу бічної поверхні.
Учні: 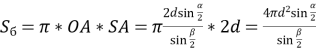 .
.
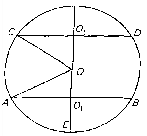
Розглянемо формування аналізу та синтезу на високому рівні при розв’язуванні такої задачі: “Радіуси основ кульового пояса дорівнюють 10 см і 12 см, а його висота – 11 см. Знайти поверхню сферичного пояса, якщо паралельні площини, які перетинають кулю, розміщені по різні боки від центра кулі”.
Виконаємо малюнок:
Проведемо аналіз цієї задачі, використовуючи такий загальний прийом евристичної діяльності, як аналіз:
Нехай АСDВА – осьовий переріз даного пояса, О1 і О2 – центри його основ, Н1=О1Е і Н2=О2F – висота кульових сегментів АВЕ і СDF.
Площа поверхні сферичного пояса дорівнює площі сфери, від якого віднімаються площі сферичних сегментів, розміщених поза поясом. Площа сферичного сегмента знаходиться за формулою S=2πRН. Проведемо О1О2![]()
Синтез: Оскільки точка О лежить між О1 і О2, то ОО2=11-ОО1, тому з ∆ОО1А і ∆ОО2С маємо:
АО12+ОО12=СО22+(11-ОО1)2.
144+ОО12=100+121-22*ОО1+ОО12, ОО1=7/2, ОО2=15/2.
![]() (см).
(см).
Н1=ОЕ-ОО1=9 (см), Н2=ОF-ОО2=5 (см).
![]() (см2),
(см2),
![]() (см2).
(см2).
![]() (см2),
(см2),
![]() (см2).
(см2).
Отже, використовуючи аналіз та синтез, ми розв’язали поставлену перед нами задачу.
Розв’язуючи задачу “Радіуси двох куль – 25 дм і 29 дм, а відстань між їх центрами – 36 дм. Знайти довжину лінії, по якій перетинаються їх поверхні”, учні під керівництвом вчителя спочатку пригадують операційний склад прийому аналізу і синтезу, потім виконують роздільне відпрацювання операцій та складання ООД під керівництвом вчителя:
- Аналіз (проводимо аналіз задачі, використовуючи прийом аналізу). Встановити мету: обчислити довжину лінії по якій перетинаються дані кулі.
- Пригадати означення кулі, кола, перерізу кулі, що проходить через її центр.
- Скласти план. Учні ставлять перед собою питання: “Як знайти довжину лінії по якій перетинаються дані кулі?”. Відповідають, що потрібно знайти радіус даного перерізу.
-
Оскільки О1О2=36<25+29, то поверхні двох куль перетинаються по колу. Розглянемо переріз поверхонь цих куль довільною площиною, яка проходить через пряму їх центрів. Ця площина перетинає кожну поверхню по її великому колу, які перетинатимуться в точках А і В. О1О2
- Сформулювати висновок: “Оскільки ми чітко визначили, що нам дано і що потрібно знайти, то ми можемо безпосередньо відшуковувати потрібні нам величини і підставити дані з умови в отримані формули”.
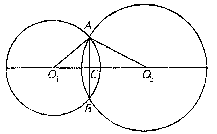
Переходимо до роздільного відпрацювання операцій (використовуємо загальний евристичний прийом – синтез):
- З ∆О1АС (<С=900) АС2=О1А-О1С2=252-х2.
- З ∆О2АС (<С=900): АС2=О2А2-О2С2=292-(36-х)2.
- Звідси: 252-х2=292-(36-х)2, х=15 (дм).
-
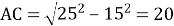 (дм).
(дм).
- Коло (С, СА) матиме довжину 2π*СА=2π*20=40π (дм).
Отже, ми відшукали довжину лінії по якій перетинаються поверхні двох куль.
Як бачимо, при розв’язуванні задач на високому рівні досить зручно використовувати загальні прийоми евристичної діяльності. Вони допомагають проводити допоміжні міркування, узагальнювати задачу чи конкретизувати її, розв’язувати стереометричні задачі, порівнюючи їх з планіметричними задачами.
Такі прийоми евристичної діяльності, як свідчить практика, стимулюють в учнів бажання вчитися, а саме головне – міркувати та висловлювати свої думки, навіть, якщо вони можуть бути не зовсім вірні. При цьому ввесь клас бере активну участь у бесіді і відшукані правильних методів розв’язання задачі. Крім цього, використання аналізу і синтезу при розв’язувані задач високого рівня стимулює в учнів розвиток творчого мислення.
Висновки
Використання в навчальному процесі спеціально підібраних евристичних задач є однією з основних умов рівневого розв’язання задач на використання загальних прийомів евристичної діяльності старшокласників на уроках стереометрії.
Особливістю евристичної діяльності учнів є фактор відкриття, який має, як правило, лише суб’єктивну значущість. Евристики в більшості випадків не усвідомлюються учнями, вони злиті з результатами дій, оскільки увага учнів зосереджується на пошуку розв’язання задачі. Тому для поглиблення рівня абстрагованості евристик доцільно застосовувати евристичні задачі. Розвиток евристичної діяльності являє собою сходження на структурні рівні, де обсяг свідомого та логічно впорядкованого знання зростає.
Дібрана система задач сприяє розвитку евристичної діяльності учнів за рахунок того, що вона базується на принципах евристичності, наочності, максимальної зацікавленості, поступового нарощування складності та відповідає таким вимогам: раціонального співвідношення між логічним та евристичним компонентами навчальної діяльності; відповідності життєвій практиці учнів; забезпеченню рівневої диференціації навчання; повноті представлення евристик.
Отже, формування в старшокласників загальних прийомів евристичної діяльності при розв’язувані задач сприяє свідомому засвоєнню ними теоретичного матеріалу, активному розв’язуванню задач різних типів, що значною мірою активізує евристичну діяльність учнів та підвищує рівень навчальних досягнень учнів.
Перелік використаної літератури
- Балк Г.Д. О применении эвристических приемов в школьном преподавании математики/Г.Д.Балк. – Математика в школе, 1969, № 5 – с. 21-29.
- Барыбин К.С. Сборник геометрических задач на доказательство/К.С.Барыбин. – М.: Учпедгиз, 1954 – 152 с.
- Бевз Г.П. Геометрія 10-11: Підручник для 10-11 класів загальноосвітніх навчальних закладів/Г.П.Бевз, В.Г.Бевз, Н.Г.Владімірова. – К.: Вежа, 2001 – 224 с.
- Бурда М.І. Диференціація у навчанні математики: методичні рекомендації/М.І.Бурда. – К.: УОП КДПІ, 1992 – 98 с.
- Власенко К.В. Формування прийомів евристичної діяльності на уроках геометрії/К.В.Власенко. – К.: Рідна школа, 2003, №7 – с. 41-43.
- Гайшут О.Г. Геометрія: Збірник задач/О.Г.Гайшут. – К.: “Кімо”, 2008.
- Горчакова I.А. Система математичних задач як засіб формування евристичної діяльності учнів основної школи/I.А.Горчакова. – К., 2002 – 226с.
- Істер О.С. Тематичні контрольні роботи та завдання для корекції знань з геометрії/О.С.Істер. – Кам’янець-Подільський: “Абетка” – 2004 – 64с.
- Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10-11 кл. серед. шк. – 5-те вид./О.В. Погорєлов. – К.: Освіта, 2001 – 128 с.
- Сморжевський Л.О. Стереометрія. Дидактичні матеріали та тематичні перевірочні роботи для рівневого навчання/Л.О.Сморжевський, Ю.Л.Сморжевський. – Кам’янець-Подільський: “Абетка-нова”, 2002 – 68 с.
- Сморжевський Ю.Л. Прийоми евристичної діяльності учнів при вивченні геометрії. Диференційовані завдання/Ю.Л.Сморжевський. – Кам’янець-Подільський: Абетка, 2004 – 100 с.
1


про публікацію авторської розробки
Додати розробку
