Властивості множення раціональних чисел.

Тема. Властивості множення раціональних чисел.

Мета: повторити відомі учням властивості множення натуральних та дробових чисел, поширити їх на множення раціональних чисел і вдоско­налити вміння виконувати множення раціональних чисел (використо­вуючи переставну, сполучну та властивості 0 та 1 при множенні)

Тип уроку: систематизація та узагальнення знань, умінь, навичок

Хід уроку

I. Перевірка домашнього завдання

Математичний диктант 1 [2]

1. Знайдіть добуток 2 на -3 [-7 на -5].
2. Помножте -3 на (-1,7) [-0,3 на 1,7].
3. Розв'яжіть рівняння .
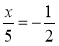
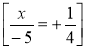4. Обчисліть значення виразу -0,4 · .

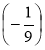
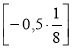II. Актуалізація опорних знань

Усні вправи

1. Обчисліть значення виразів 0,3 · 5; 4 · 0,5; 50 · 0,02; 2,9 · 10; 31 · 0,01.
2. Обчисліть значення виразів найзручнішим способом

а) 25 · 32 · 0,4; б) 0,5 · 28 · 0,2; в) · 3,75 · ; г) 3,45 · 0,28 · 0 · 2,49

3. Спростіть вирази а) 2х · 3,5; б) 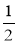х · 4;  в) 0,3х · 0,4у
4. Які числа треба підставити замість *, щоб рівності стали правильними⁹
   а) 3,75 · * = 3,75; б)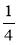 · * = 1; в) 2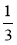· * = 0; г) * · 0 = 0.

III. Узагальнення знань

  Єдине, що повинні засвоїти учнів на цьому уроці — це реалізація принципу загальності та послідовності у викладенні навчального матеріалу, а саме

1. властивості множення, що були вивчені у 5 класі, «працюють» не
   тільки в натуральних числах, а й з будь-якими раціональними числами,
2. вивчивши алгоритми виконання будь-якої арифметичної дії, ми
   неодмінно повинні знайти відповідь на запитання «А чи не можна
   цю дію за даним алгоритмом виконати більш зручним способом?»

Тому на цьому етапі уроку нам треба ще раз наголосити на тому, що всі властивості (обов'язково проговорити і записати відповідні рівності) множення ми можемо використовувати і в роботі з раціональними чис­лами. Але є ще один момент — знак добутку кількох раціональних чи­сел, на який треба додатково звернути увагу.

Результатом обговорення теоретичних питань уроку можуть бути такі записи, виконані на дошці та в зошитах учнів.

IV. Вдосконалення вмінь

Усні вправи

1. Знайдіть знак добутку: а) (-2)·(-7)·5·(-9); б) (+9)·(-2)·3·(-8)·(-7)·(-1).
2. Додатним чи від'ємним буде добуток:

а) трьох від'ємних чисел;

б) трьох чисел, з яких два від'ємні, а одне додатне;

в) трьох чисел, з яких одне від'ємне, два додатні;

г) чотирьох від'ємних чисел?

3. Виконайте множення:

а) -3 · 0;  б) (-19) · 1;  в) 0,25 · (-3) · (-4)

     0 · 13     1 · (-27)     -1,25 · (-3) · (-8)

   -5 · (-17) · 0;         +15 · (-1)     .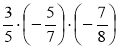

   -1 · (-2);

Письмові вправи

1. Обчисліть:

1) а) - 0,25 · (- 7) · 8; б) 4 · 0,01 · (- 1,5); в) 7 · 2,5 · (- 16); г) 0,45 · 11 ·(-8);

    д) 3 · (-6,5) · (-4); є) -0,125 · 13 · (-8).

2) а) ·(-5)·1;  б) ·8·3; в) ·(-4)· 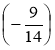; г) -12··;      

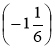    д) ··14; є) -4··.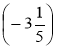

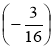3) а) - 125 · 1,5 · (- 8) · 6; б) - 4 · (- 0,4) · 79 · (- 5) · (- 25);

     в) - 5 · (- 2,5) · (- 1,25) · (- 64); г) - 0,5 · (- 625) · 20 · (- 1,6).

 Звертаємо увагу на те, що спочатку визначаємо знак добутку,

а потім виконуємо множення модулів у «зручному» порядку.

2. * Перемножимо всі цілі числа від -1 до -5 включно. Чи буде добуток більший від 100?
3. Обчисліть значення виразу найраціональнішим способом:

а) -5·(2,5+(-2,5))·5; б) -2,87·3,5··.

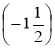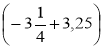4. Розв'яжіть рівняння: а) -3,2х = 0; б) -3,2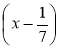= 0; в) (х - 3) 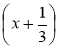= 0;
   г) х(х – 0,5) = 0; д) х(х - 0,3)(х+ 0,5)·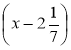 = 0.

V. Підсумок уроку

Заповніть пропуски так, щоб рівності стали правильними:

ab = …; (ab)c = …; a ·...= a; a · ... = - a; a ·...= 0;

...1 · ...2 · ...3 = -6;  ...1 · ... 2 · ... 3 = 6.

VI. Домашнє завдання

1. Обчисліть: а) 25 · (-7,02) · 4; б) -8 · 4,8 · (-2,5); в) 0 ,75 · 3,3 · (-40);

г) 0,9 · (-8) · 15 · (-5); д) 6 · (-4,5) · (-4) · 25; є) -1,125 · 3 · (-8) · 11;

ж) 21 · · 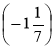; з) - · · 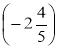45; и) - · · 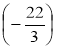(-54).

2. Перший насос наповнює басейн за 20 хв, а другий — за 30 хв. За який
   час наповнять басейн насоси, працюючи разом?